「組合せ」に関する様々な問題の考え方を知りましょう。
問題文に「選ぶ」という言葉があれば分かりやすいかもしれませんが,すべての問題に「選ぶ」と書かれているわけではありません。
問題文をしっかり読んで適切に対応することが必要です。
様々な問題がありますが,ここでは四角形の個数を求める有名問題を考えてみよう。
Contents
四角形の個数を求める問題
問題4本の平行線と,それらに交わる5本の平行線とによってできる平行四辺形は何個あるか。



ヒロ
1つの平行四辺形を決めるためには「何を決めているのか」を把握することが重要だね。
【考え方と解答】
次の斜線部分で示したように,具体的に1つの平行四辺形を考える。

この平行四辺形を考えたときに「何を決めたのか」をしっかり考えよう。平行な2直線を2組決めることで1つの平行四辺形が決まることが分かる。
4本の平行線にA~Dの名前を付け,それらに交わる5本の平行線にa~eの名前を付ける。
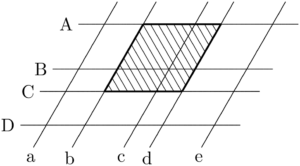
斜線で示した平行四辺形の場合,A~Dの4本からAとCの2本を選び,a~eの5本かbとdの2本を選んだとみなすことができる。
つまり,次の2つの手順で平行四辺形を決めることができる。
① A~Dの4本から2本を選ぶ。
② a~eの5本から2本を選ぶ。
①の方法は $\nCk{4}{2}$ 通りあり,②の方法は $\nCk{5}{2}$ 通りあるから,求める平行四辺形の個数は
次の斜線部分で示したように,具体的に1つの平行四辺形を考える。

この平行四辺形を考えたときに「何を決めたのか」をしっかり考えよう。平行な2直線を2組決めることで1つの平行四辺形が決まることが分かる。
4本の平行線にA~Dの名前を付け,それらに交わる5本の平行線にa~eの名前を付ける。

斜線で示した平行四辺形の場合,A~Dの4本からAとCの2本を選び,a~eの5本かbとdの2本を選んだとみなすことができる。
つまり,次の2つの手順で平行四辺形を決めることができる。
① A~Dの4本から2本を選ぶ。
② a~eの5本から2本を選ぶ。
①の方法は $\nCk{4}{2}$ 通りあり,②の方法は $\nCk{5}{2}$ 通りあるから,求める平行四辺形の個数は
\begin{align*}
\nCk{4}{2}\times\nCk{5}{2}=6\times10=60~個
\end{align*}
\nCk{4}{2}\times\nCk{5}{2}=6\times10=60~個
\end{align*}
四角形の個数を求める問題2
問題図のように正方形の各辺を8等分し,各辺に平行線を引くことによってつくられるゲーム盤がある。これらの平行線によって作られる正方形でない長方形の総数を求めよ。



ヒロ
求めるものは正方形でない長方形の総数であるが,正方形を含めた長方形の総数を求める方が楽だね。

ヒロ
また,正方形の総数を求めるのも楽そうだね。
【考え方と解答】
正方形を含めた長方形は次の2つの手順で作ることができる。
① 9本の横線から2本を選ぶ。
② 9本の縦線から2本を選ぶ。
①の方法は $\nCk{9}{2}$ 通りあり,②の方法も $\nCk{9}{2}$ 通りあるから,
隣り合う2本の直線の間隔を1として,正方形の1辺の長さに着目して数えていく。9本の横線を上からA, B, C, D, E, F, G, H, Iとし,9本の縦線を左からa, b, c, d, e, f, g, h, iとする。
例えば1辺の長さが1の正方形を考えると,次の図のような斜線で示した正方形が考えられる。
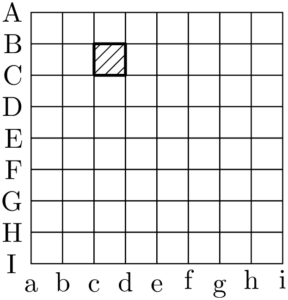
斜線の正方形の場合は,隣り合ったBとCの横線を選び,隣り合ったcとdの縦線を選んだことになる。隣り合う横線の選び方は,上側の横線の選び方に等しく,A~Hの8通りある。縦線の選び方も同様に8通りあるから,1辺の長さが1の正方形の個数は $8^2=64$ 個ある。
また1辺の長さが2の正方形を考えると,次の図のようなピンクで塗った正方形が考えられる。
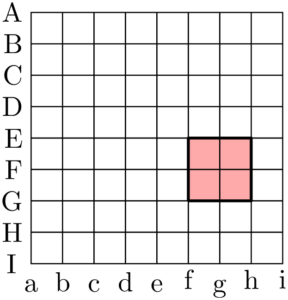
この場合はEとGの横線を選び,fとgの縦線を選んだことになる。間隔が2になる横線の選び方は,上側の横線の選び方がA~Gの7通りある。縦線の選び方も7通りあるから,1辺の長さが2の正方形の個数は $7^2=49$ 個ある。
このように1辺の長さを1ずつ大きくしていくと,横線と縦線の選び方が1ずつ少なくなることが分かる。
したがって,正方形の総数は
正方形を含めた長方形は次の2つの手順で作ることができる。
① 9本の横線から2本を選ぶ。
② 9本の縦線から2本を選ぶ。
①の方法は $\nCk{9}{2}$ 通りあり,②の方法も $\nCk{9}{2}$ 通りあるから,
\begin{align*}
(\nCk{9}{2})^2=36^2=1296~個
\end{align*}
次に正方形の総数を数える。(\nCk{9}{2})^2=36^2=1296~個
\end{align*}
隣り合う2本の直線の間隔を1として,正方形の1辺の長さに着目して数えていく。9本の横線を上からA, B, C, D, E, F, G, H, Iとし,9本の縦線を左からa, b, c, d, e, f, g, h, iとする。
例えば1辺の長さが1の正方形を考えると,次の図のような斜線で示した正方形が考えられる。

斜線の正方形の場合は,隣り合ったBとCの横線を選び,隣り合ったcとdの縦線を選んだことになる。隣り合う横線の選び方は,上側の横線の選び方に等しく,A~Hの8通りある。縦線の選び方も同様に8通りあるから,1辺の長さが1の正方形の個数は $8^2=64$ 個ある。
また1辺の長さが2の正方形を考えると,次の図のようなピンクで塗った正方形が考えられる。

この場合はEとGの横線を選び,fとgの縦線を選んだことになる。間隔が2になる横線の選び方は,上側の横線の選び方がA~Gの7通りある。縦線の選び方も7通りあるから,1辺の長さが2の正方形の個数は $7^2=49$ 個ある。
このように1辺の長さを1ずつ大きくしていくと,横線と縦線の選び方が1ずつ少なくなることが分かる。
したがって,正方形の総数は
\begin{align*}
&8^2+7^2+6^2+5^2+4^2+3^2+2^2+1^2 \\[4pt]
&=64+49+36+25+16+9+4+1 \\[4pt]
&=204~個
\end{align*}
以上より,正方形でない長方形は&8^2+7^2+6^2+5^2+4^2+3^2+2^2+1^2 \\[4pt]
&=64+49+36+25+16+9+4+1 \\[4pt]
&=204~個
\end{align*}
\begin{align*}
1296-204=1092~個
\end{align*}
1296-204=1092~個
\end{align*}


















