【数学ⅡB】円が通過する領域【早稲田大・山口大・日本女子大】

Contents

ページ1
ページ2
1 2019年早稲田大
ページ3
1 2011年山口大
ページ4
1 2015年日本女子大

2015年日本女子大

2015年日本女子大正の実数 $t$ に対して方程式

\begin{align*}
x^2+y^2-2tx-4ty+4t^2=0
\end{align*}

で表される円を $C_t$ とする。$t$ がどのような値でも $C_t$ と接する直線の方程式を求めよ。

【考え方と解答】
まずは，円 $C_t$ がどのような円かを知るために，中心と半径を求めよう。
$x^2+y^2-2tx-4ty+4t^2=0$ より

\begin{align*}
(x-t)^2+(y-2t)^2=t^2
\end{align*}

となる。$t>0$ より，円 $C_t$ の中心は $(t,~2t)$ で，半径は $t$ である。
直線 $l:ax+by+c=0$（$a$ と $b$ は同時に0にならない）が $t$ の値にかかわらず $C_t$ と接するとすると，直線 $l$ と点 $(t,~2t)$ との距離が $t$ であるから

\begin{align*}
&\dfrac{\abs{at+4bt+c}}{\sqrt{a^2+b^2}}=t \\[4pt]
&\abs{(a+4b)t+c}=\sqrt{a^2+b^2}t
\end{align*}

両辺を2乗すると

\begin{align*}
&\{(a+2b)t+c\}^2=(a^2+b^2)t^2 \\[4pt]
&(a+2b)^2t^2+2(a+2b)ct+c^2=(a^2+b^2)t^2 \\[4pt]
&(4ab+3b^2)t^2+2(a+2b)ct+c^2=0
\end{align*}

これが $t$ の値にかかわらず成り立つのは

\begin{align*}
\begin{cases}
4ab+3b^2=0 &~\cdots\cdots① \\[4pt]
(a+2b)c=0 &~\cdots\cdots② \\[4pt]
c^2=0 &~\cdots\cdots③
\end{cases}
\end{align*}

が成り立つときである。
③より，$c=0$ となり，このとき，②は必ず成り立つ。
①より，

\begin{align*}
&b(4a+3b)=0 \\[4pt]
&b=0~または~b=-\dfrac{4}{3}a
\end{align*}

$b=0$ のとき，$a\neq0$ であるから，直線 $l$ の方程式は

\begin{align*}
&ax=0 \\[4pt]
&x=0
\end{align*}

$b=-\dfrac{4}{3}a$ のとき，直線 $l$ の方程式は

\begin{align*}
&ax-\dfrac{4}{3}a=0 \\[4pt]
&3x-4y=0
\end{align*}

したがって，求める直線の方程式は

\begin{align*}
x=0,~3x-4y=0
\end{align*}

ヒロ

下のアニメーションを見ることで，円 $C_t$ が $x=0$（$y$ 軸）と直線 $3x-4y=0$ に接しながら動くことが確認できる。

ヒロ

別解として，次のような考え方をすることもできる。

【別の考え方と解答】
　$C_t$ は中心 $(t,~2t)$，半径 $t$ の円であり，$t$ の値と円 $C_t$ は1対1対応する。つまり，$t$ の値と接点の座標も1対1対応する。言い換えると，接点を通るような $t$ は1つだけ存在すると言える。接点を $(X,~Y)$ とすると

\begin{align*}
X^2+Y^2-2tX-4tY+4t^2=0
\end{align*}

が成り立ち，$t$ の方程式とみて変形すると次のようになる。

\begin{align*}
4t^2-2(X+2Y)t+X^2+Y^2=0
\end{align*}

これをみたす $t$ はただ1つであるから，判別式を $D$ とすると，$D=0$ となる。よって，

\begin{align*}
&\dfrac{D}{4}=(X+2Y)^2-4(X^2+Y^2)=0 \\[4pt]
&-3X^2+4XY=0 \\[4pt]
&X(3X-4Y)=0 \\[4pt]
&X=0,~3X-4Y=0
\end{align*}

したがって，接点は2直線 $x=0$，$3x-4y=0$ 上にある。つまり，円 $C_t$ は2直線 $x=0$，$3x-4y=0$ に接しながら動く。

ヒロ

もしかすると，次のように考えた人が最も多いかもしれない。

【考え方と解答】
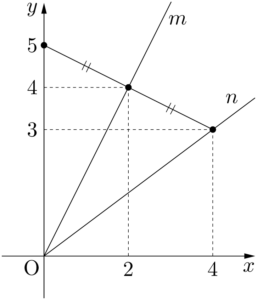
　$C_t$ は中心 $(t,~2t)$，半径 $t$ の円であるから，$t$ の値にかかわらず円 $C_t$ は $y$ 軸に接する。また，中心は直線 $m:y=2x$ 上にあるから，円 $C_t$ は直線 $m$ に関して $y$ 軸を対称移動した直線 $n$ とも接する。直線 $m$ と $y$ 軸は原点で交わるから，直線 $n$ は原点を通る直線である。
　また，直線 $m$ の傾きが2であるから，$m$ 上の点 $(2,~4)$ を通り $m$ に垂直な直線を考えると，

\begin{align*}
&y=-\dfrac{1}{2}(x-2)+4 \\[4pt]
&y=-\dfrac{1}{2}x+5
\end{align*}

となるから，この直線は $y$ 軸と点 $(0,~5)$ で交わる。よって，点 $(0,~5)$ を点 $(2,~4)$ に関して対称移動させた点は $(4,~3)$ である。したがって，直線 $n$ の方程式は $y=\dfrac{3}{4}x$ である。
　つまり，円 $C_t$ は $t$ の値にかかわらず，2直線 $x=0$，$y=\dfrac{4}{3}x$ と接している。
※$m$ 上の点として $(2,~4)$ を選んだのは，$m$ に垂直な直線の傾きが $-\dfrac{1}{2}$ であり，$y$ 軸との交点の $y$ 座標が整数として得られることが簡単な計算で分かるからである。