Contents
- ページ1
- ページ2
- 1 2019年 早稲田大
- ページ3
- 1 2011年 山口大
- ページ4
- 1 2015年 日本女子大
2019年 早稲田大
2019年 早稲田大$k$ を実数とする。座標平面において方程式
(1) $C$ が円であるような $k$ の値の範囲を求めよ。ただし,点も円とみなすものとする。
(2) $k$ が変化するとき,$C$ が通る点 $(x,~y)$ の存在領域を座標平面上に図示せよ。
(3) (2)で求めた領域の境界線と(1)で求めた円が共有点をもたないような,$k$ の値の範囲を求めよ。
\begin{align*}
x^2+y^2+x+(2k+1)y+k^2+1=0
\end{align*}
の表す図形 $C$ を考える。次の問に答えよ。x^2+y^2+x+(2k+1)y+k^2+1=0
\end{align*}
(1) $C$ が円であるような $k$ の値の範囲を求めよ。ただし,点も円とみなすものとする。
(2) $k$ が変化するとき,$C$ が通る点 $(x,~y)$ の存在領域を座標平面上に図示せよ。
(3) (2)で求めた領域の境界線と(1)で求めた円が共有点をもたないような,$k$ の値の範囲を求めよ。
【(1)の考え方と解答】
平方完成して考えよう。$x^2+y^2+x+(2k+1)y+k^2+1=0$ より
平方完成して考えよう。$x^2+y^2+x+(2k+1)y+k^2+1=0$ より
\begin{align*}
\left(x+\dfrac{1}{2}\right)^2+\left(y+k+\dfrac{1}{2}\right)^2=k-\dfrac{1}{2}
\end{align*}
これが円であるのは $k-\dfrac{1}{2}\geqq0$ が成り立つときであるから,求める $k$ の値の範囲は\left(x+\dfrac{1}{2}\right)^2+\left(y+k+\dfrac{1}{2}\right)^2=k-\dfrac{1}{2}
\end{align*}
\begin{align*}
k\geqq\dfrac{1}{2}
\end{align*}
k\geqq\dfrac{1}{2}
\end{align*}
(2) $k$ が変化するとき,$C$ が通る点 $(x,~y)$ の存在領域を座標平面上に図示せよ。
【(2)の考え方と解答】
$C$ が点 $(X,~Y)$ を通るとすると
$C$ が点 $(X,~Y)$ を通るとすると
\begin{align*}
X^2+Y^2+X+(2k+1)Y+k^2+1=0~\cdots\cdots①
\end{align*}
が成り立つ。いま,$k$ は実数であるから,①を $k$ の2次方程式とみてX^2+Y^2+X+(2k+1)Y+k^2+1=0~\cdots\cdots①
\end{align*}
\begin{align*}
k^2+2Yk+X^2+Y^2+X+Y+1=0~\cdots\cdots②
\end{align*}
と変形すると,②は実数解をもつ。判別式を $D$ とすると $D\geqq0$ が成り立つからk^2+2Yk+X^2+Y^2+X+Y+1=0~\cdots\cdots②
\end{align*}
\begin{align*}
&\dfrac{D}{4}=Y^2-(X^2+Y^2+X+Y+1)\geqq0 \\[4pt]
&Y\leqq-X^2-X-1
\end{align*}
よって,$C$ が通る点 $(X,~Y)$ は放物線 $y=-x^2-x-1$ の下側(境界を含む)にあることが分かる。&\dfrac{D}{4}=Y^2-(X^2+Y^2+X+Y+1)\geqq0 \\[4pt]
&Y\leqq-X^2-X-1
\end{align*}
\begin{align*}
y&=-x^2-x-1 \\[4pt]
&=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}~\cdots\cdots③
\end{align*}
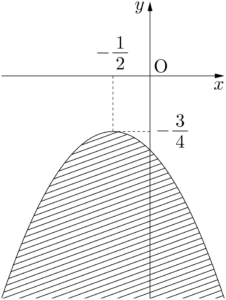
となるから,$C$ が通る点 $(x,~y)$ の存在領域は,下図の斜線部分(境界を含む)である。y&=-x^2-x-1 \\[4pt]
&=-\left(x+\dfrac{1}{2}\right)^2-\dfrac{3}{4}~\cdots\cdots③
\end{align*}


ヒロ
下のアニメーションを見ることで,円 $C$ が放物線の下側をどのように通過していくかを確認することができる。
(3) (2)で求めた領域の境界線と(1)で求めた円が共有点をもたないような,$k$ の値の範囲を求めよ。
【(3)の考え方と解答】
$C$ の方程式と $y=-x^2-x-1$ を連立して $x$ を消去すると
③より,$y\leqq-\dfrac{3}{4}$ であるから,$-k>-\dfrac{3}{4}$ のときは共有点をもたない。
(1)で求めた $k$ の範囲を考えると,求める $k$ の値の範囲は
$C$ の方程式と $y=-x^2-x-1$ を連立して $x$ を消去すると
\begin{align*}
&y^2+2ky+k^2=0 \\[4pt]
&(y+k)^2=0 \\[4pt]
&y=-k
\end{align*}
よって,$C$ と放物線 $y=-x^2-x-1$ は $y=-k$ となる点で共有点をもつ。&y^2+2ky+k^2=0 \\[4pt]
&(y+k)^2=0 \\[4pt]
&y=-k
\end{align*}
③より,$y\leqq-\dfrac{3}{4}$ であるから,$-k>-\dfrac{3}{4}$ のときは共有点をもたない。
(1)で求めた $k$ の範囲を考えると,求める $k$ の値の範囲は
\begin{align*}
\dfrac{1}{2}\leqq k<=\dfrac{3}{4}
\end{align*}
\dfrac{1}{2}\leqq k<=\dfrac{3}{4}
\end{align*}

ヒロ
下のアニメーションを見ることで,円 $C$ が放物線と共有点をもたずに動くことが確認できる。


















