ここでは,弧度法と度数法について説明します。
新しい角度の単位である「rad(ラジアン)」を使いこなせるようになることが重要です。
単位の変換公式を利用するだけでなく,感覚的な理解をすることで,弧度法の便利さを実感することができるでしょう。
Contents
弧度法とは

ヒロ
角度を表すときの単位として「$30\Deg$」のように「度(°)」を使ってきた。

ヒロ
しかし,ここでは新しい角度の単位「ラジアン(rad)」を使う。

ヒロ
単位が変わるため,1ドルが1円ではないように,1°が1radにはならない。

ヒロ
まぁ,そんなことになるならラジアンを使う意味もないだろう。

ヒロ
これまで使ってきた「°」は度数法で表したときの単位であり,「rad」は弧度法で表したときの単位である。

ヒロ
結論から書くと,度数法と弧度法の対応は次のようになっている。
度数法と弧度法の対応$180\Deg=\pi$(rad) である。ほとんどの場合,単位の「rad」を省略して書かれる。

ヒロ
弧度法は弧の長さと角度を対応させた考え方である。
半径1の円では,弧の長さがそのまま角の大きさになる。例えば,半円の弧の長さは $\pi$ であるから,中心角も $\pi$(rad)である。これが180°を弧度法で表すと $\pi$(rad)になる理由である。四分円(中心角が90°の扇形)の弧の長さは $\dfrac{\pi}{2}$ であるから,90°を弧度法で表した場合は $\dfrac{\pi}{2}$(rad)となる。
逆に考えると,弧の長さが1であるような扇形を考えると,その中心角は1(rad)となる。
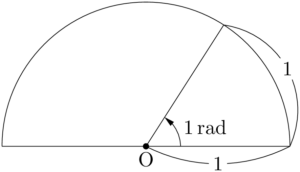
ちなみに1(rad)は度数法で表すと,$\left(\dfrac{180}{\pi}\right)\Deg$ であり,小数で表すと約53.7°である。

ヒロ
まずは弧度法で表された角を見たときに,どのような角であるかが瞬時に分かるようにすることが重要だろう。




















