センター試験の数学IAの図形問題の考え方を説明します。センター試験の数学IAの選択問題では,場合の数と確率・整数の性質・図形の性質の3項目から2項目選択して解答することになっています。
図形の問題を勉強するときに困ることの1つは図の描き方ではないでしょうか?解答・解説に描かれている図を見れば,「なるほど!」と理解できても「そもそもその図が描けないから困ってるんだけど・・・」という人もいると思います。
ここでは図の描き方の1つの方法を提案するとともに,センター試験ならではの解法を説明します。
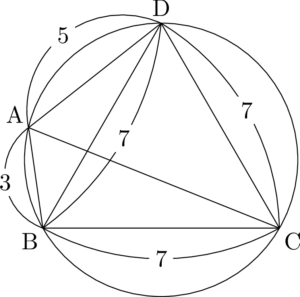
\mathrm{AB=3,~BC=7,~CD=7,~DA=5}
\end{align*}
(1) $\kaku{A}=\myBox{アイウ}\Deg$ であり,$\mathrm{BD}=\myBox{エ},~\mathrm{AC}=\myBox{オ}$ である。また,四角形ABCDの面積は $\myBox{カキ}\sqrt{\myBox{ク}}$ である。
(2) 対角線AC,BDの交点をEとするとき
\sin\kaku{AEB}=\dfrac{\myBox{ケ}\sqrt{\myBox{コ}}}{\myBox{サ}}
\end{align*}
Contents
できるだけ正確に図を描く方法
「最初は適当で良い」と言われても,その適当な描き方すら分からないからどうしようもないということですね。
ここでは,図の描き方の1つの例を示していきます。また,出来る限り条件に合うように正確に描く方法を説明します。そのためには,まずは円をできるだけキレイに描けるようにしてください。

まずは図を描こう。今回は四角形が円に内接しているから,先に円を描こう。

円を描いたら,次はその円に内接するように四角形ABCDを描いていこう。僕は基本的に,最も長い辺が水平になるようにして,他の点はその辺より上側になるように描くようにしている。だから今回はBCが水平になるように描いていこう。
※あくまでもこれは基本であって,一旦図を描いてみて,描く角度を変えた方が良いと判断した場合は描き直すこともあります。

ここで,円の中心より上側に描くか下側に描くかは他の辺の長さに関係する。例えば,BCを円の中心より上側に描くと次のようになる。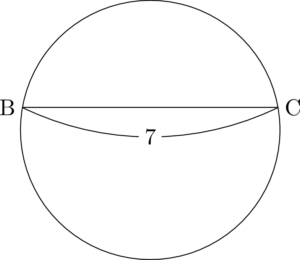

残りの2点A,DをBCの上側の円周上に描こうとするが,この場合は $\mathrm{CD}=7$ となるように点Dをとることができない。したがって,辺BCが円の中心より下側になるように描かないといけないことが分かる。

ということで,BCを円の中心より下側に描いてみて?

はい!描きました。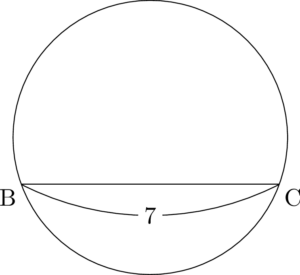

次に点Dをとろう。ここで $\mathrm{BC}=7$ だから,BCと長さが等しくなるようにしよう。

点Dをとりました。
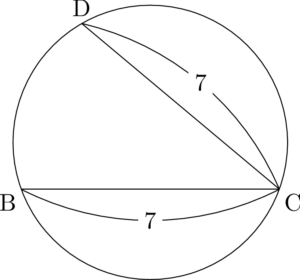

あとは $\mathrm{AB}=3,~\mathrm{AD}=5$ となるように点Aをとろう。しかし,この図ではBD間が短くて条件に合うように点Aをとれないね。それらしく点Aをとったとしても次のようになる。
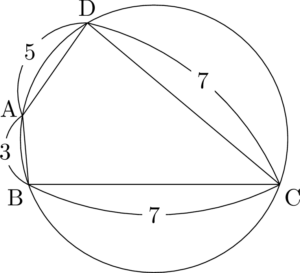

これではとても $\mathrm{BC}=7$ で $\mathrm{AB}=3$ だと言われても,そう見えないね。

確かにABとBCだけ見ても,長さが変ですね。

こうなったのはBCが円の中心に近かったのが原因だから,BCを円の中心からもう少し離して描き直そう。

BCを描き直しました。
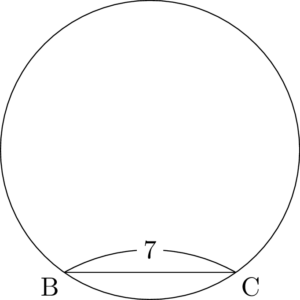

点Dをとってみて?

こうなりました。
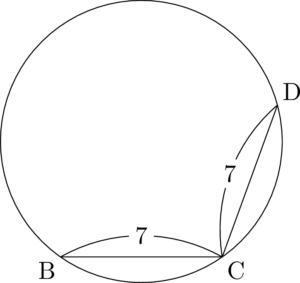

これは・・・

もう気付いてるね。この時点で失敗だと分かるけど,点Aをとると次のようになる。
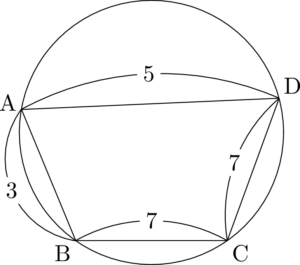

BCは円の中心より下側にないといけないけど,近すぎても遠すぎても,本来の図にはならない。

めちゃくちゃ難しいんですけど・・・

こういったところに時間をかけすぎると意味がないわけで,速く修正できるようにしよう。

頑張ります。

ちなみに正確に描くと次のようになる。
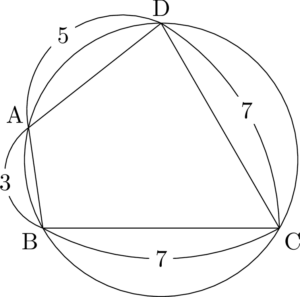

手描きだと,ここまでキレイには描けないけど,それなりに描く努力はできると思う。
角の大きさと辺の長さを求める問題の考え方

それでは(1)の $\kaku{A}$ から求めていこう。

$\kaku{A}$ の大きさを聞かれているから,$\kaku{A}$ を含む三角形を探そう。今回は $\sankaku{ABC}$ で考えれば良いね。
\mathrm{BD}^2&=3^2+5^2-2\Cdota3\Cdota5\cos A \\[4pt]
&=34-30\cos A~\cdots\cdots ①
\end{align*}

BDも分からないから,方程式がもう1本必要だね。そこでBDを含む三角形を考えると,$\sankaku{BCD}$ が見つかる。さらに四角形ABCDが円に内接しているから,$C=180\Deg-A$ が成り立つ。
\mathrm{BD}^2&=7^7+7^2-2\Cdota7\Cdota7\cos(180\Deg-A) \\[4pt]
&=98+98\cos A~\cdots\cdots ②
\end{align*}

これで方程式が2本になったから,BDと $\cos A$ を求められる。
&64+128\cos A=0 \\[4pt]
&\cos A=-\dfrac{1}{2}
\end{align*}
①より
\mathrm{BD}^2=34-30\Cdota\left(-\dfrac{1}{2}\right)=49
\end{align*}

$\sankaku{BCD}$ って正三角形だったんですね。

そうだね。最初に描いた図で三角形BCDが正三角形に見えるなら,うまく描けてたということ。

次はACを求めよう。

$\sankaku{ABC}$ と $\sankaku{ACD}$ に着目して余弦定理で式を立てて連立すれば解けますね。
\mathrm{AC}^2&=3^2+7^2-2\Cdota3\Cdota7\cos B \\[4pt]
&=58-42\cos B~\cdots\cdots ③ \\[4pt]
\mathrm{AC}^2&=7^7+5^2-2\Cdota7\Cdota5\cos(180\Deg-B) \\[4pt]
&=74+70\cos B~\cdots\cdots ④
\end{align*}
&16+112\cos B=0 \\[4pt]
&\cos B=-\dfrac{1}{7}
\end{align*}
\mathrm{AC}^2=74+70\Cdota\left(-\dfrac{1}{7}\right)=64
\end{align*}
多角形の面積の求め方

次は四角形ABCDの面積を求めよう。

四角形ABCDを2つの三角形 $\sankaku{ABD}$ と $\sankaku{BCD}$ に分割して面積を求めよう。

それでは,次の図を見て四角形ABCDの面積を求めよう。
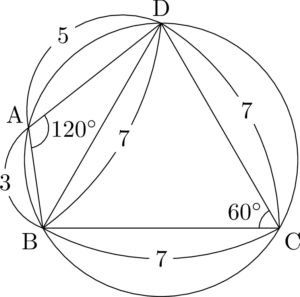
S&=\sankaku{ABD}+\sankaku{BCD} \\[4pt]
&=\dfrac{1}{2}\Cdota3\Cdota5\sin120\Deg+\dfrac{1}{2}\Cdota7\Cdota7\sin60\Deg \\[4pt]
&=\dfrac{15}{2}\Cdota\dfrac{\sqrt{3}}{2}+\dfrac{49}{2}\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&=\dfrac{64\sqrt{3}}{4}=16\sqrt{3}
\end{align*}
$\sin$ の値の求め方【気付かない角の二等分線】

次は(2)を解こう。どうやって求める?

$\sin\kaku{AEB}$ の値を求める問題だから,$\kaku{AEB}$ を含む三角形ABEを考えれば良いんじゃないですか?

じゃあ,その方針でやってみよう。$\sin$ を求めたいのだから,正弦定理を利用することを考えれば良いね。

$\kaku{AEB}$ の対辺ABの長さが分かっているから,もう1組の角と対辺の長さを求めれば良いんですね。

ここで,BCとCDの長さが等しいことから,あることに気付かないといけない。
図のように,円周上に6つの点A, B, C, D, E, Fがあり,$\mathrm{BC=EF}$のとき,
\kaku{BAC}=\kaku{EDF}
\end{align*}

最も気付きにくいものは下図のように2つの三角形がくっついているものである。$\mathrm{BC=CD}$ という条件から,ACが $\kaku{BAD}$ の二等分線になっていることに気付かなければならない。その後,角の二等分線の性質を使う問題に発展することが多い。
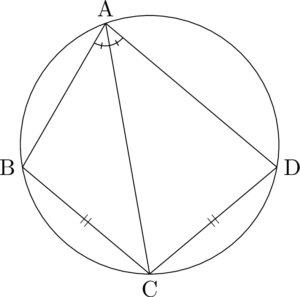

なるほど。言われれば分かりますけど,それじゃ意味ないですからね。自分で気付けるように頑張ります。

図形問題において,隣り合う辺の長さが等しい場合は,「どうせ角の二等分線に関する問題を出すんだろ?」と思えるくらいになろう。

これで $\kaku{BAE}$ の大きさが分かるね。

$\kaku{A}=120\Deg$ だから $\kaku{BAE}=60\Deg$ です。

そうだね。あとはその対辺BEの長さを求めよう。

$\kaku{BAE}$ が分かったのはACが $\kaku{A}$ の二等分線だと分かったからだね。そして点Eは,その角の二等分線とBDの交点になっている。角の二等分線の性質を知っていればBEは分かるね。

大丈夫です。
&\mathrm{BE:ED}=3:5 \\[4pt]
&\mathrm{BE}=\dfrac{3}{8}\mathrm{BD}=\dfrac{21}{8}
\end{align*}
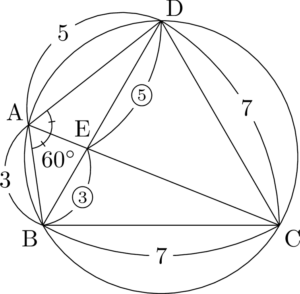

これで $\sin\kaku{AEB}$ を求められるね。
&\dfrac{\mathrm{BE}}{\sin\kaku{BAE}}=\dfrac{\mathrm{AB}}{\sin\kaku{AEB}} \\[4pt]
&\mathrm{AB}\sin\kaku{BAE}=\mathrm{BE}\sin\kaku{AEB} \\[4pt]
&3\sin60\Deg=\dfrac{21}{8}\sin\kaku{AEB} \\[4pt]
&\sin\kaku{AEB}=3\Cdota\dfrac{\sqrt{3}}{2}\Cdota\dfrac{8}{21} \\[4pt]
&\sin\kaku{AEB}=\dfrac{4\sqrt{3}}{7}
\end{align*}
速く解くためには知識が必要【名古屋三角形】

今回の問題は,今から約20年も前の問題だけど,この頃のセンター試験は今のセンター試験みたいに誘導でガチガチに固められてはいなかった。

確かに最近のセンターと違ってあっさりしてますね。

1つの問題でも,その答えに至る過程は,解く人によって変わるのは当たり前で,知識の幅広さや深さによって,計算が大幅に楽になることもある。

ということで,ここからが本番。センター数学の空欄のルールと様々な知識をフル活用して解いてみよう。

実は最初の $\kaku{A}$ はすぐに $120\Deg$ と分かる。

通常は最初に説明した通り,これは余弦定理を利用して $\cos A$ を求めた上で $A$ を求める典型的な問題だと分かる。

$\cos A$ の値を求めた上で $A$ を求めるのなら,$A$ は三角定規に関連する有名角となることが確定。しかも空欄から鈍角と分かるから,$\cos A$ の値は $-\dfrac{1}{2},~-\dfrac{1}{\sqrt{2}},~-\dfrac{\sqrt{3}}{2}$ のいずれかになる。

ここで空欄からBDも整数であることが分かるから,三角形ABDは3つの辺がすべて整数である三角形となる。つまり余弦定理を用いると $\cos A$ が有理数になることが確定する。

$\cos A$ は $-\dfrac{1}{2},~-\dfrac{1}{\sqrt{2}},~-\dfrac{\sqrt{3}}{2}$ の中の有理数となるから,$\cos A=-\dfrac{1}{2}$ となるしかなく,$A=120\Deg$ と求まる。

数学がある程度得意な人なら,余弦定理で $\cos A$ を計算しているときに,計算結果が有理数になることは明らかだから「これ $-\dfrac{1}{2}$ になって,$A=120\Deg$ だな」ってどこかで思ったはず。

確かに・・・でも,BDとACはどうするんですか?

それは $A=120\Deg$ だと思った時点で,$\mathrm{BD}=7$ ということが分かって,そのあとすぐに $\mathrm{AC}=8$ も分かる。一言で言えば「知っているから」だよ。

どういうことですか?

例えば次の図の $x$ の値はどうなる?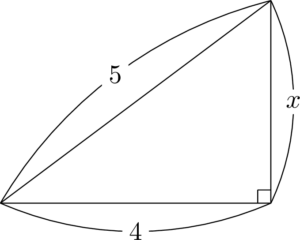

3ですよね?

そうだね。それは計算して求めてないよね?

$3:4:5$ の直角三角形ですよね。見てすぐに分かりました。

「知っている三角形」だから計算しなくても分かるんだよね。ということは知っている三角形を増やせば良いね。

なるほど

センター試験で出題される三角形として都合が良いのは,辺の長さが整数で,角は $30\Deg,45\Deg,~$$60\Deg,120\Deg,~$$135\Deg,150\Deg$ のいずれかであるもの。このような条件を満たす頻出三角形を覚えてしまおう。
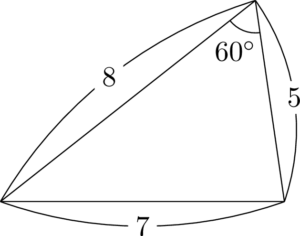
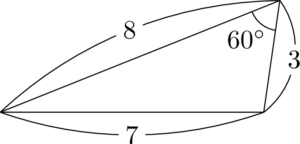


上から順に「名古屋で悩み,七五三」と覚えよう。758で名古屋,783で悩み,753で七五三。7の対角が $60\Deg$ か $120\Deg$ になっている。

ちなみに3つの三角形を組み合わせると次のようになる。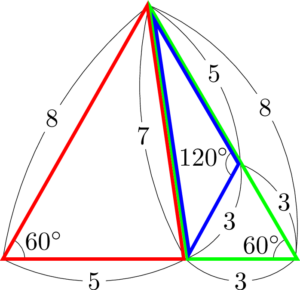

キレイですね!

今回の問題は $\mathrm{AB=3,~AD=5},~$$A=120\Deg$ が分かった時点で,2辺とその間の角が決まったので三角形が1つに決まるはず。七五三の三角形を知っていれば,計算することなく $\mathrm{BD}=7$ だと分かる。

ここまでで $\sankaku{BCD}$ が正三角形であることも分かっているため,かなり正確に描くことができる。
$A=60\Deg$ の $\sankaku{ABC}$ が円に内接する図を描くときは,次のようにしよう。
①まず,円を描く。円の中心からまっすぐ下に直線を引き,円との交点をPとする。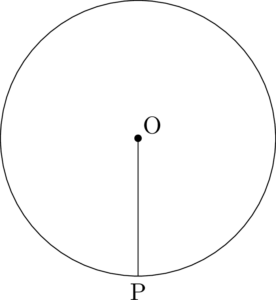
②OPの中点をMとする。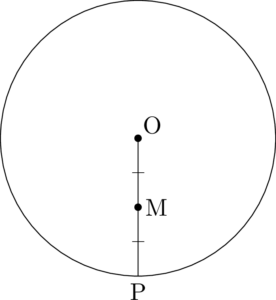
③Mを通りOPと垂直な直線を引いて,円との交点をB,Cとする。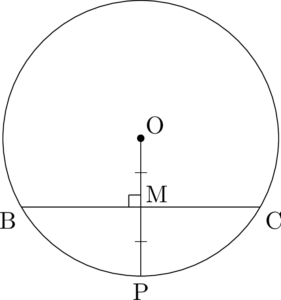
④BCより上側の円周上に点Aをとると,$\kaku{BAC}=60\Deg$となる。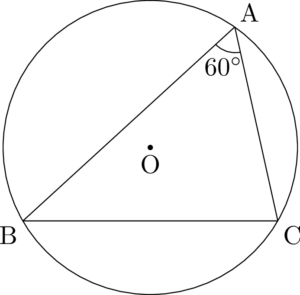

さらに,$\sankaku{ABC}$ と $\sankaku{ACD}$ は3辺が整数で7の対角が $60\Deg$ の三角形だから,名古屋三角形と悩み三角形を知っていれば $\mathrm{AC}=8$ も分かる。

ちなみにこの知識がなくても,トレミーの定理を知っていればACを簡単に求めることができる。
円周上に4点A, B, C, Dがあるとき,
\mathrm{AB\Cdota CD+BC\Cdota DA=AC\Cdota BD}
\end{align*}
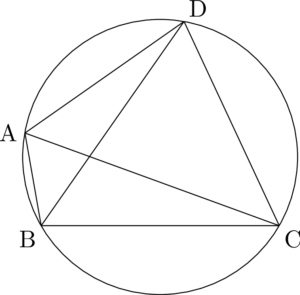

「対辺の積の和は対角線の積に等しい」と覚えよう。個別試験で証明問題として出題されることもある。最近では,2018年岐阜薬科大学で出題されている。
&7\Cdota \mathrm{AC}=5\Cdota7+3\Cdota7 \\[4pt]
&\mathrm{AC}=8
\end{align*}

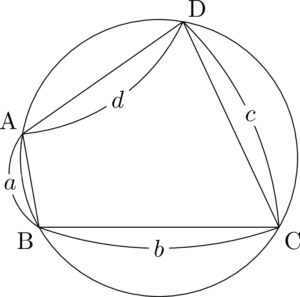
四角形ABCDの面積については,2つの三角形に分けて求めれば良いが,ブラーマグプタの公式を紹介しておく。
円周上に4点A, B, C, Dがあるとき,四角形ABCDの面積 $S$ は,$s=\dfrac{a+b+c+d}{2}$ とすると,
S=\sqrt{(s-a)(s-b)(s-c)(s-d)}
\end{align*}
特に,$d=0$ のとき,四角形ABCDは $\sankaku{ABC}$ となる。このとき,$s=\dfrac{a+b+c}{2}$となり,$\sankaku{ABC}$ の面積 $S$ は
S=\sqrt{s(s-a)(s-b)(s-c)}
\end{align*}

これもトレミーの定理と同様,個別試験で証明問題として出題されることがある。最近では,2019年京都府立大学で出題されている。
S&=\sqrt{(11-3)(11-5)(11-7)^2} \\[4pt]
&=\sqrt{8\Cdota6\Cdota4^2}=16\sqrt3
\end{align*}

(2)は(1)で四角形ABCDの面積を求めたんだから,それを利用して求めよう。
下図の四角形ABCDの面積 $S$ は,
S=\dfrac{1}{2}\mathrm{AC\Cdota BD}\sin\theta
\end{align*}
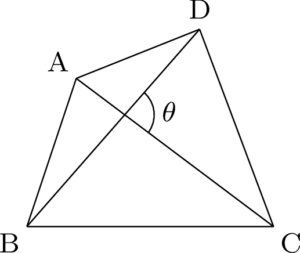

この公式はどこにでも載ってる有名な公式なので,しっかり覚えて使いこなせるようにしよう。ここでは省略するが,証明できるようにしておこう。
\sin\kaku{AEB}&=\dfrac{2S}{\mathrm{AC}\Cdot\mathrm{BD}} \\[4pt]
&=\dfrac{2\Cdot16\sqrt{3}}{8\Cdot7} \\[4pt]
&=\dfrac{4\sqrt{3}}{7}
\end{align*}

知らない定理と公式が多すぎて処理が追いつきません・・・

少しずつで良いから,使える定理と公式を増やしていこう。
まとめ

図形の問題では,図が正確であれば楽に解けることが多いので,日頃から正確な図を描くようにしよう。

外接円が関連する場合,必ず円から描くようにしよう。その際に,1つの角が $60\Deg$ のときは,円さえキレイに描くことができれば,かなり正確に三角形を内接させることができる。

細かすぎると思うかもしれないが,正確に図を描くことで,今まで解けなかった問題を解けるようになることもある。頑張ろう!




















