平均変化率について説明します。
平均変化率とは何かを知らなければ,「平均変化率を求めよ。」と言われても何を求めれば良いか分からないから,どうしようもありません。
数学用語については正しく知っておくことが重要です。
Contents
平均変化率とは
まずは「平均変化率」の意味を知っておこう。
平均変化率とは 関数 $y=f(x)$ において,$y$ の変化量 $f(b)-f(a)$ の $x$ の変化量 $b-a$ に対する割合
ここで $y=f(x)$ のグラフとの関連を確認しておこう。$y=f(x)$ のグラフを $C$ とし,$C$ 上に2点A$(a,~f(a))$,B$(b,~f(b))$ をとる。
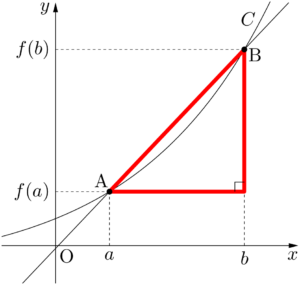
$\dfrac{f(b)-f(a)}{b-a}$ は直線ABの傾きを表していることが分かる。つまり,平均変化率を求める計算は傾きを求める計算に置き換えることができる。
\begin{align*}
\dfrac{f(b)-f(a)}{b-a}~(a\neq b)
\end{align*}
を $x$ が $a$ から $b$ まで変化するときの,関数 $f(x)$ の平均変化率という。\dfrac{f(b)-f(a)}{b-a}~(a\neq b)
\end{align*}
ここで $y=f(x)$ のグラフとの関連を確認しておこう。$y=f(x)$ のグラフを $C$ とし,$C$ 上に2点A$(a,~f(a))$,B$(b,~f(b))$ をとる。

$\dfrac{f(b)-f(a)}{b-a}$ は直線ABの傾きを表していることが分かる。つまり,平均変化率を求める計算は傾きを求める計算に置き換えることができる。

ヒロ
「率」は割合を表すのだから,変化率は変化の割合($x$ が1増加するときに $y$ がどれだけ増加するか)を表していることになる。

ヒロ
平均変化率は変化率の平均ということであるから,変化する最初と最後の変化の割合が平均変化率ということになる。

ヒロ
このように解釈すれば,平均変化率の計算方法も忘れないかもしれない。


















