【数学ⅡB】放物線と円で囲まれた部分の面積【摂南大】

放物線と円で囲まれた部分の面積を求める方法を説明します。

円が関係する図形の面積を求める場合は，扇形と三角形の組み合わせを考えて計算することが重要です。

すべてを定積分で求めようとすると，無理関数の積分計算が必要となり，計算が大変になります。

また，そもそも無理関数の積分ができない場合は，式を立てても結局計算できないため，面積を求めることができなくなります。

そういう事態を防ぐためにも，図形の組み合わせ方を知って慣れることが重要でしょう。

2020年 摂南大

ヒロ

円と放物線の共有点の個数についての基礎知識は，次の記事から手に入れよう。

【数学ⅡB】円と放物線の共有点【金沢大・立命館大・岩手大】

ここでは円と放物線の共有点について説明します。 この記事では，放物線の軸が円の中心を通っている状況について扱うことにします。 「円と放物線の共有点」の問題を苦手とする人が多いですが，落ち着いて考えることができるようになりましょう。 円と放物...

methodology.site

2020.09.23

【(1)の解答と考え方】
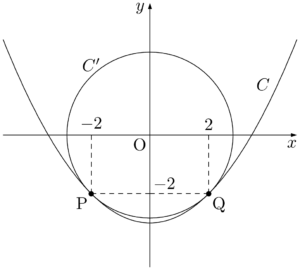
$C’$ の方程式を $x^2+y^2=r^2~(r>0)$ とおく。$C:x^2=4y+12$ であるから，$C,~C’$ から $x$ を消去すると

\begin{align*}
&(4y+12)+y^2=r^2 \\[4pt]&y^2+4y+12-r^2=0~\cdots\cdots①
\end{align*}

2曲線 $C,~C’$ が相異なる2点P，Qで接線を共有するのは，①が $y>-3$ をみたす重解をもつときである。①の判別式を $D$ とすると

\begin{align*}
\dfrac{D}{4}&=4-(12-r^2) \\[4pt]&=r^2-8
\end{align*}

$D=0$ のとき，$r=2\sqrt{2}$ であり，このとき，①の重解は $y=-2$ となり $y>-3$ をみたす。
よって，円 $C’$ の半径は $2\sqrt{2}$ である。
【参考図】

(2) P，Qによって分けられる円 $C’$ の弧のうち，長さの短い方を $D$ とする。$C$ と $D$ が囲む部分の面積は $\dfrac{\myhako}{\myhako}-\myhako\;\pi$ である。

【(2)の解答と考え方】
求める面積 $S$ は図の色を塗った部分の面積である。

三角形POQは直角二等辺三角形であることが分かるから，

\begin{align*}
\sankaku{POQ}=\dfrac{1}{2}\Cdota4\Cdota2=4
\end{align*}

となる。扇形POQの面積 $T_1$ は

\begin{align*}
T_1=\dfrac{1}{2}\Cdota2^2\Cdota\dfrac{\pi}{2}=\pi
\end{align*}

また，$y=-2$ と $D$ で囲まれた部分の面積 $T_2$ は6分の1公式を用いて

\begin{align*}
T_2=\dfrac{1}{6}\Cdota\dfrac{1}{4}\Cdota4^3=\dfrac{8}{3}
\end{align*}

であるから

\begin{align*}
S&=T_1+\sankaku{POQ}-T_2 \\[4pt]&=\dfrac{8}{3}+4-\pi \\[4pt]&=\dfrac{20}{3}-\pi
\end{align*}