ここでは格子点の個数について説明します。
まず,格子点とはx座標とy座標がともに整数の点のことです。
ある領域内に含まれる格子点の個数を求める問題は多くの大学で出題されます。座標軸に平行な直線上にある格子点の個数を求めることによって,その領域に含まれる格子点の個数を求める方法が基本的な解法となります。
他にも漸化式を立ててそれを解くことによって格子点の個数を求める方法もあるため,様々な問題を解いて,その解法を知ることが重要です。
Contents
2020年 鳥取大
2020年 鳥取大自然数 $n$ に対して,直線 $x+4y=4n$,$x=0$,$y=0$ で囲まれる三角形の周および内部にある点で,$x$ 座標と $y$ 座標がともに整数である点の個数を求めよ。
プリントを次のリンクからダウンロードできます。
【解答と考え方】
考えている格子点は,図の灰色部分(領域 $D$ とする)に含まれる格子点である。
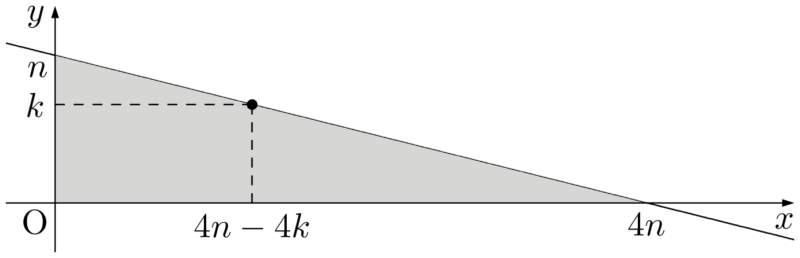
どっちの座標軸に平行な直線で考えると解きやすいかを考えよう。この問題では $x$ 軸に平行な直線で考えると,境界線との交点の座標が格子点になるから考えやすいことが分かる。
領域 $D$ 内の直線 $y=k$ 上の格子点の座標は $(l,~k)~(l=0,~1,~2,~\cdots,~4n-4k)$ と表されるから,直線 $y=k$ 上の格子点の個数は $4n-4k+1$ である。
よって,領域 $D$ 内に含まれる格子点の個数は
考えている格子点は,図の灰色部分(領域 $D$ とする)に含まれる格子点である。

どっちの座標軸に平行な直線で考えると解きやすいかを考えよう。この問題では $x$ 軸に平行な直線で考えると,境界線との交点の座標が格子点になるから考えやすいことが分かる。
領域 $D$ 内の直線 $y=k$ 上の格子点の座標は $(l,~k)~(l=0,~1,~2,~\cdots,~4n-4k)$ と表されるから,直線 $y=k$ 上の格子点の個数は $4n-4k+1$ である。
よって,領域 $D$ 内に含まれる格子点の個数は
\begin{align*}
\Sum{k=0}{n}(4n-4k+1)&=\dfrac{(4n+1)+1}{2}\Cdota(n+1) \\[4pt]
&=(2n+1)(n+1)
\end{align*}
\Sum{k=0}{n}(4n-4k+1)&=\dfrac{(4n+1)+1}{2}\Cdota(n+1) \\[4pt]
&=(2n+1)(n+1)
\end{align*}
2018年 津田塾大
2018年 津田塾大$n$ を自然数とする。$xy$ 平面において,次の連立方程式の表す領域を $D_n$ とする。
(1) $n=3$ のときの領域 $D_3$ を図示せよ。また,$S_3$ の値を求めよ。
(2) $n\geqq1$ のとき
(i) $k$ を $0\leqq k\leqq n$ を満たす整数とする。$D_n$ の内部および周上において,$x$ 座標の値が $k$ に等しい格子点の個数を $k,~n$ の式で表せ。
(ii) $S_n$ を $n$ の式で表せ。
\begin{align*}
x\geqq0,~x\leqq n,~y\geqq2^x,~y\leqq2^n
\end{align*}
$D_n$ の内部および周上における格子点,つまり $x$ 座標と $y$ 座標がともに整数である点の個数を $S_n$ とするとき,以下の問いに答えよ。x\geqq0,~x\leqq n,~y\geqq2^x,~y\leqq2^n
\end{align*}
(1) $n=3$ のときの領域 $D_3$ を図示せよ。また,$S_3$ の値を求めよ。
(2) $n\geqq1$ のとき
(i) $k$ を $0\leqq k\leqq n$ を満たす整数とする。$D_n$ の内部および周上において,$x$ 座標の値が $k$ に等しい格子点の個数を $k,~n$ の式で表せ。
(ii) $S_n$ を $n$ の式で表せ。
【(1)の解答と考え方】
$D_3$ を表す不等式は

上図の格子点を数えて,$S_3=21$
$D_3$ を表す不等式は
\begin{align*}
x\geqq0,~x\leqq3,~y\geqq2^x,~y\leqq8
\end{align*}
となるから,$D_3$ は図の灰色部分である。x\geqq0,~x\leqq3,~y\geqq2^x,~y\leqq8
\end{align*}

上図の格子点を数えて,$S_3=21$
(i) $k$ を $0\leqq k\leqq n$ を満たす整数とする。$D_n$ の内部および周上において,$x$ 座標の値が $k$ に等しい格子点の個数を $k,~n$ の式で表せ。
【(2)(i)の解答と考え方】
領域 $D_n$ 内で直線 $x=k$ 上の格子点の座標は $(k,~l)~(l=2^k,~2^k+1,~\cdots,~2^n)$ であるから,直線 $x=k$ 上の格子点の個数は
領域 $D_n$ 内で直線 $x=k$ 上の格子点の座標は $(k,~l)~(l=2^k,~2^k+1,~\cdots,~2^n)$ であるから,直線 $x=k$ 上の格子点の個数は
\begin{align*}
2^n-2^k+1~個
\end{align*}
2^n-2^k+1~個
\end{align*}
(ii) $S_n$ を $n$ の式で表せ。
【(2)(ii)の解答と考え方】
\begin{align*} S_n&=\Sum{k=0}{n}(2^n-2^k+1) \\[4pt] &=(2^n+1)(n+1)-\dfrac{2^{n+1}-1}{2-1} \\[4pt] &=(n-1)2^n+n+2 \end{align*}


















