ここでは定点を通る直線について説明します。
数学が苦手な人にとって,直線の方程式の係数に文字が含まれているときは嫌な気分になるでしょう。
それはその文字の値が変化すると,直線が動いて考えるのが難しくなるからでしょう。
何の規則もなく動くように見える直線の中には,文字の値にかかわらず動かない点(定点)を通る場合があります。
その定点を見付けることができれば,少しは考えやすくなるかもしれません。
この記事を読んで,考え方と定点の見つけ方をマスターしましょう。
Contents
直線が定点を通るとは

ヒロ
簡単な例で「定点を通る直線」を理解しよう。
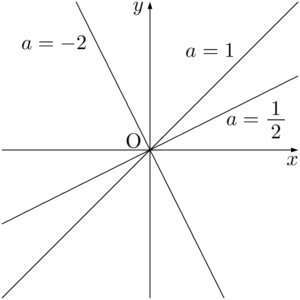
直線は通る1点と傾きが決まれば,ただ1つに決まるから,「定点を通る」という条件をみたすのは傾きだけが変化するときである。「直線 $l:y=ax$($a$ は定数)はどのような直線か?」と聞かれれば,「$l$ は原点を通り,傾きが $a$ の直線だ」と答えるだろう。通る点に着目すると,$a$ がどのような値であっても,その値に関係なく,$l$ は原点を通る。
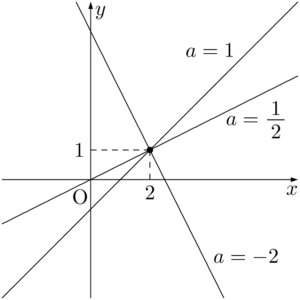
このグラフを平行移動することで,定点も同じ分だけ平行移動されるため,定点の位置を自由に決めることができる。例えば,常に点$(2,~1)$ を通るような直線を考えると,$y=ax$ のグラフを $x$ 軸方向に2,$y$ 軸方向に1だけ平行移動すれば良いから直線の方程式は
\begin{align*}
y=a(x-2)+1
\end{align*}
となる。グラフは次のようになる。y=a(x-2)+1
\end{align*}

ヒロ
上の例から次のことが言えることが理解できるだろう。
定点を通る直線の方程式$y=a(x-p)+q$ で表される直線は,点$(p,~q)$ を通り,傾きが $a$ の直線である。

ヒロ
ちなみに「平行移動」と聞くと「$y-q=a(x-p)$」の形でないと分かりにくいという人がいるが,公式を頼りにし過ぎている気がする。

ヒロ
$y=a(x-p)$ の時点で,$x$ に $p$ を代入すると $y=0$ となるから,このままだと点$(p,~0)$ を通ることになる。$x=p$ のときに $y=q$ となれば良いのだから,後ろに $q$ を加えて $y=a(x-p)+q$ とすれば良いだけである。

ヒロ
ここには平行移動などという考えはなく,条件を満たすように式を変えているだけである。

ヒロ
公式や平行移動の考え方は非常に重要であるが,このような式だけで考える方法を知っておくことも重要である。

ヒロ
要するに「考え方の引き出し」を多く持った方が有利であるということ。
定点を通る直線に関する問題
2012年 神戸学院大関数 $y=-ax+2a$ のグラフは,$a$ の値にかかわらずある点を必ず通る。その点をAとすると,点Aの座標は $\left(\myhako,~\myhako\right)$ である。
プリントを次のリンクからダウンロードできます。
【考え方と解答】
グラフの方程式から,与えられた関数のグラフは傾きが $-a$ の直線であることが分かる。右辺を $-a$ でくくると
よって,A$(2,~0)$ である。
グラフの方程式から,与えられた関数のグラフは傾きが $-a$ の直線であることが分かる。右辺を $-a$ でくくると
\begin{align*}
y=-a(x-2)
\end{align*}
となるから,グラフは $a$ の値にかかわらず,点$(2,~0)$ を通る。y=-a(x-2)
\end{align*}
よって,A$(2,~0)$ である。


















