ここでは多角形の周上を動く点の位置に関する確率について解説します。
正三角形や正六角形の周上を動く点の位置に関する確率を求める問題が良く出題されます。
様々な問題がありますが,実際に定期テストで出題された問題を通して,考え方を理解して多角形の周上の動点に関する確率に強くなりましょう。
正三角形の周上を動く点の位置に関する確率
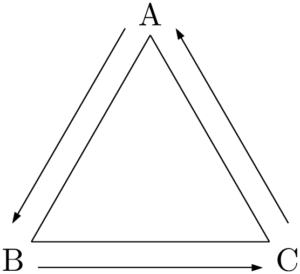
問題次の図で点PはAを出発点とし,さいころを投げて矢印の向きに移動する。偶数の目が出たらその数だけ進み,奇数の目が出たら1つ進む。次に,もう1回さいころを投げて,Pに移った点を出発点として,同様に移動する。2回の移動後に,PがBにある確率を求めよ。

【考え方と解答】
点Xから点Yに移る確率を $P(X\to Y)$ と表すことにする。
点Aから点Aに移るのは,6の目が出るときだから,$P(A\to A)=\dfrac{1}{6}$ となる。
点Aから点Bに移るのは,1, 3, 4, 5のいずれかの目が出るときであるから,$P(A\to B)=\dfrac{4}{6}=\dfrac{2}{3}$ となる。
点Aから点Cに移るのは,2の目が出るときだから,$P(A\to C)=\dfrac{1}{6}$ となる。
対称性を考えると
(i) A→A→B
(ii) A→B→B
(iii) A→C→B
(i)のときの確率は
点Xから点Yに移る確率を $P(X\to Y)$ と表すことにする。
点Aから点Aに移るのは,6の目が出るときだから,$P(A\to A)=\dfrac{1}{6}$ となる。
点Aから点Bに移るのは,1, 3, 4, 5のいずれかの目が出るときであるから,$P(A\to B)=\dfrac{4}{6}=\dfrac{2}{3}$ となる。
点Aから点Cに移るのは,2の目が出るときだから,$P(A\to C)=\dfrac{1}{6}$ となる。
対称性を考えると
\begin{align*}
&P(B\to A)=\dfrac{1}{6},~P(B\to B)=\dfrac{1}{6},~P(B\to C)=\dfrac{2}{3} \\[4pt]
&P(C\to A)=\dfrac{2}{3},~P(C\to B)=\dfrac{1}{6},~P(C\to A)=\dfrac{1}{6}
\end{align*}
PがAを出発し,2回の移動後にPがBにあるのは次の3つの場合に限られる。&P(B\to A)=\dfrac{1}{6},~P(B\to B)=\dfrac{1}{6},~P(B\to C)=\dfrac{2}{3} \\[4pt]
&P(C\to A)=\dfrac{2}{3},~P(C\to B)=\dfrac{1}{6},~P(C\to A)=\dfrac{1}{6}
\end{align*}
(i) A→A→B
(ii) A→B→B
(iii) A→C→B
(i)のときの確率は
\begin{align*}
&P(A\to A)\times P(A\to B) \\[4pt]
&=\dfrac{1}{6}\times\dfrac{2}{3} \\[4pt]
&=\dfrac{1}{9}
\end{align*}
(ii)のときの確率は&P(A\to A)\times P(A\to B) \\[4pt]
&=\dfrac{1}{6}\times\dfrac{2}{3} \\[4pt]
&=\dfrac{1}{9}
\end{align*}
\begin{align*}
&P(A\to B)\times P(B\to B) \\[4pt]
&=\dfrac{2}{3}\times\dfrac{1}{6} \\[4pt]
&=\dfrac{1}{9}
\end{align*}
(iii)のときの確率は&P(A\to B)\times P(B\to B) \\[4pt]
&=\dfrac{2}{3}\times\dfrac{1}{6} \\[4pt]
&=\dfrac{1}{9}
\end{align*}
\begin{align*}
&P(A\to C)\times P(C\to B) \\[4pt]
&=\dfrac{1}{6}\times\dfrac{1}{6} \\[4pt]
&=\dfrac{1}{36}
\end{align*}
(i)~(iii)より,求める確率は&P(A\to C)\times P(C\to B) \\[4pt]
&=\dfrac{1}{6}\times\dfrac{1}{6} \\[4pt]
&=\dfrac{1}{36}
\end{align*}
\begin{align*}
&\dfrac{1}{9}+\dfrac{1}{9}+\dfrac{1}{36} \\[4pt]
&=\dfrac{9}{36}=\dfrac{1}{4}
\end{align*}
&\dfrac{1}{9}+\dfrac{1}{9}+\dfrac{1}{36} \\[4pt]
&=\dfrac{9}{36}=\dfrac{1}{4}
\end{align*}

ヒロ
上で書いたように,すべての移動の確率を書くのが面倒な人は書き方を工夫しよう。

ヒロ
「元の点に移る確率」「1つ先の点に移る確率」「2つ先の点に移る確率」と書くことで3つにまとめて書くことができる。
正六角形の周上を動く点の位置に関する確率
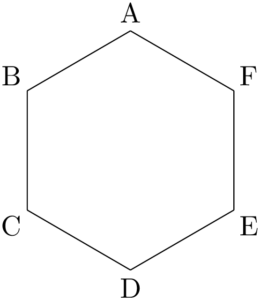
問題正六角形ABCDEFの頂点を動く点Pが点Aの位置にある。1個のさいころを投げて,1, 2の目が出たときにはPは右回りに2個次の点へ移り,3, 4, 5, 6の目が出たときには左回りに1個次の点に進む。6回投げたときに点Pが点Aにいる確率を求めよ。

【考え方と解答】
1個のさいころを投げて,1, 2の目が出る確率は $\dfrac{2}{6}=\dfrac{1}{3}$ であり,3, 4, 5, 6の目が出る確率は $\dfrac{4}{6}=\dfrac{2}{3}$ である。
6回のうち,1, 2の目が出る回数を $n$ とすると点Pが点Aにいるのは,$k$ を整数として
したがって,求める確率は
1個のさいころを投げて,1, 2の目が出る確率は $\dfrac{2}{6}=\dfrac{1}{3}$ であり,3, 4, 5, 6の目が出る確率は $\dfrac{4}{6}=\dfrac{2}{3}$ である。
6回のうち,1, 2の目が出る回数を $n$ とすると点Pが点Aにいるのは,$k$ を整数として
\begin{align*}
2n-(6-n)=6k
\end{align*}
が成り立つときである。これより2n-(6-n)=6k
\end{align*}
\begin{align*}
&3n-6=6k \\[4pt]
&n-2=2k \\[4pt]
&n=2k+2
\end{align*}
$n$ は0以上6以下の整数であるから,$n=0,~2,~4,~6$ となる。&3n-6=6k \\[4pt]
&n-2=2k \\[4pt]
&n=2k+2
\end{align*}
したがって,求める確率は
\begin{align*}
&\nCk{6}{0}\left(\dfrac{2}{3}\right)^6+\nCk{6}{2}\left(\dfrac{1}{3}\right)^2\left(\dfrac{2}{3}\right)^4+\nCk{6}{4}\left(\dfrac{1}{3}\right)^4\left(\dfrac{2}{3}\right)^2+\nCk{6}{6}\left(\dfrac{1}{3}\right)^6 \\[4pt]
&=\dfrac{64+15\Cdot16+15\Cdot4+1}{3^6} \\[4pt]
&=\dfrac{365}{729}
\end{align*}
&\nCk{6}{0}\left(\dfrac{2}{3}\right)^6+\nCk{6}{2}\left(\dfrac{1}{3}\right)^2\left(\dfrac{2}{3}\right)^4+\nCk{6}{4}\left(\dfrac{1}{3}\right)^4\left(\dfrac{2}{3}\right)^2+\nCk{6}{6}\left(\dfrac{1}{3}\right)^6 \\[4pt]
&=\dfrac{64+15\Cdot16+15\Cdot4+1}{3^6} \\[4pt]
&=\dfrac{365}{729}
\end{align*}


















