図形の性質の考え方・解き方の第五弾です。第四弾に引き続き,三角比の値が与えられたときの描画について説明します。
三角比の値が与えられたときの図を描く方法を身に付けることで,出題者が最初に描いた図を描くことができる場合があります。
センター試験の数学IAの図形問題の考え方を説明します。
\mathrm{BC}=7,~\kaku{BAC}=60\Deg,~\sin\kaku{BCA}=\dfrac{4\sqrt{3}}{7}
\end{align*}
三角形ABCの外接円の半径を $R$ とすると
R=\dfrac{\myBox{ア}}{\myBox{イ}}\sqrt{\myBox{ウ}}
\end{align*}
\mathrm{AB}=\myBox{エ}
\end{align*}
また,$\mathrm{AC}=x$ とおくと
\mathrm{BC}^2=x^2-8x+\myBox{オカ}
\end{align*}
x=\myBox{キ}~~または~x=\myBox{ク}
\end{align*}
以下,$\mathrm{AC}=\mybox{ク}$ とする。
三角形ABCの面積を $S$,$\kaku{BAC}$ の二等分線と辺BCとの交点をDとすると
S=\myBox{ケコ}\sqrt{\myBox{サ}},~\mathrm{AD}=\dfrac{\myBox{シス}}{\myBox{セソ}}\sqrt{\myBox{タ}}
\end{align*}
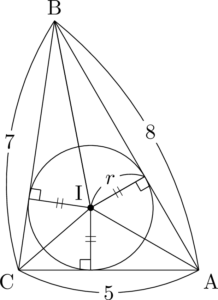
三角形ABCの内接円の中心をI,半径を $r$ とすると
r=\sqrt{\myBox{チ}}
\end{align*}
\mathrm{AH}=\myBox{ツ}
\end{align*}
\mathrm{BI}=\myBox{テ}\sqrt{\myBox{ト}}
\end{align*}
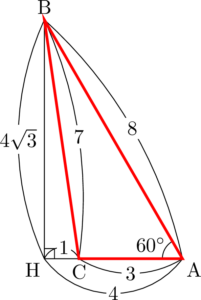
正弦の値を利用して図を描く方法

今回は $\sin C$ が与えられているので,その値を利用して図を描こう。$\sin$ の値のときは $\cos$ の値が与えられているときと違って,2種類存在することに注意しよう。

$\sin C=\dfrac{4\sqrt{3}}{7}$ だから,斜辺が7,高さが $4\sqrt{3}$ の直角三角形を描く。$\kaku{ACB}$ が鋭角のときと鈍角のときの両方を描いておこう。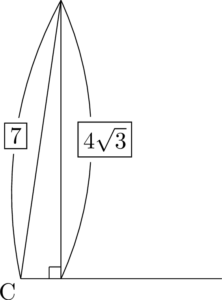
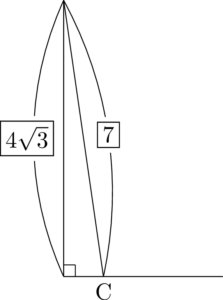

$\mathrm{BC}=7$ が与えられていて,斜辺の比の $\fbox{7}$ と一致しているから斜辺をBCとしよう。さらに三平方の定理から $\mathrm{CH}=1$ と分かる。
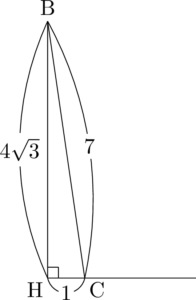

次に $\kaku{BAC}$ が $60\Deg$ となるように点Aをとる。この際に $\mathrm{AH}=4$ であることを考えて適切な位置にとる。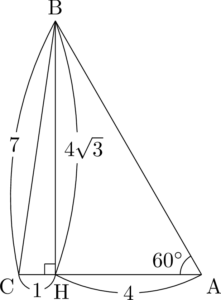
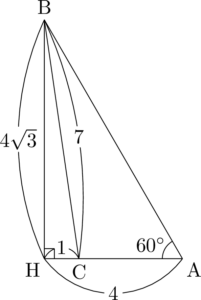

$\sankaku{ABH}$ は $1:2:\sqrt{3}$ の直角三角形だから,$\mathrm{AB}=8$ となることも分かるから,これも書き込もう。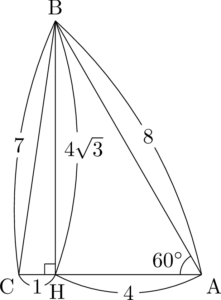
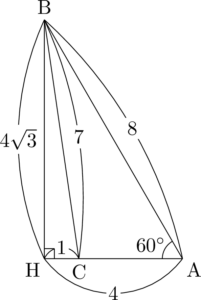
前半の解答【外接円の半径と名古屋三角形】

最初は外接円の半径を求める問題。

正弦定理ですね。
R&=\dfrac{\mathrm{BC}}{2\sin A} \\[4pt]
&=\dfrac{7}{2\sin60\Deg} \\[4pt]
&=\dfrac{7}{\sqrt{3}}=\dfrac{7}{3}\sqrt{3}
\end{align*}

次はABの長さを求める問題だけど,もう $\mathrm{AB}=8$ と分かっている。

次はACの長さを求める問題。2次方程式を立てる誘導になっている。このように2次方程式を立てる場合,余弦定理を使おう。

ただ,今回の問題では,$\myBox{オカ}$ が分からなくても,$\myBox{キ}$ と $\myBox{ク}$ は分かるね。

図を見れば名古屋三角形と悩み三角形と分かるから,ACは3か5ですね。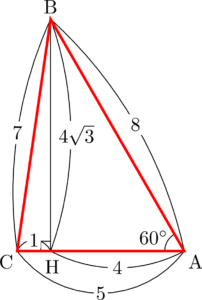

ただ,これくらいの問題なら余弦定理だなと気付いて欲しい。
\mathrm{BC}^2&=x^2+8^2-2\Cdota8x\cos60\Deg \\[4pt]
&=x^2-8x+64
\end{align*}

これで $\myBox{オカ}$ が求まった。これを解けば $x$ を求められる。
&7^2=x^2-8x+64 \\[4pt]
&x^2-8x+15=0 \\[4pt]
&(x-3)(x-5)=0 \\[4pt]
&x=3,~5
\end{align*}

それでは後半へ進もう。
【マーク模試 過去問(後半)】
以下,$\mathrm{AC}=\mybox{ク}$ とする。
三角形ABCの面積を $S$,$\kaku{BAC}$ の二等分線と辺BCとの交点をDとすると\begin{align*}である。
S=\myBox{ケコ}\sqrt{\myBox{サ}},~\mathrm{AD}=\dfrac{\myBox{シス}}{\myBox{セソ}}\sqrt{\myBox{タ}}
\end{align*}
三角形ABCの内接円の中心をI,半径を $r$ とすると\begin{align*}であり,この内接円と辺ABとの接点をHとすると
r=\sqrt{\myBox{チ}}
\end{align*}\begin{align*}であるから
\mathrm{AH}=\myBox{ツ}
\end{align*}\begin{align*}である。
\mathrm{BI}=\myBox{テ}\sqrt{\myBox{ト}}
\end{align*}
後半の解答【角の二等分線の長さと内接円の半径】

問題文に「$\mathrm{AC}=8$ とする」とあるから,名古屋三角形で考える。三角形ABCの面積は底辺も高さも分かっているから簡単だね。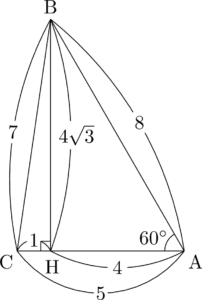
S&=\dfrac{1}{2}\Cdota5\Cdota4\sqrt{3} \\[4pt]
&=10\sqrt{3}
\end{align*}

次は角の二等分線の長さADを求める問題。$\kaku{BAC}=60\Deg$ だから $30\Deg$ ずつになる。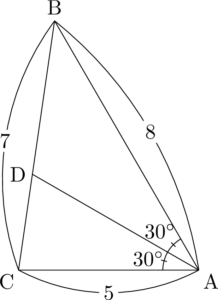

角の二等分線の長さを求める1つの方法として,三角形の面積を利用する方法がある。
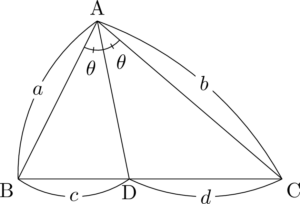
$\sankaku{ABD}+\sankaku{ACD}=\sankaku{ABC}$ より
&\dfrac{1}{2}a\Cdota\mathrm{AD}\sin\theta+\dfrac{1}{2}b\Cdota\mathrm{AD}\sin\theta=\dfrac{1}{2}ab\sin2\theta \\[4pt]
&(a+b)\mathrm{AD}\sin\theta=2ab\sin\theta\cos\theta
\end{align*}
\mathrm{AD}=\dfrac{2ab\cos\theta}{a+b}
\end{align*}

今回の問題の場合,次のようになる。
&\dfrac{1}{2}\Cdota8\Cdota\mathrm{AD}\sin30\Deg+\dfrac{1}{2}\Cdota5\Cdota\mathrm{AD}\sin30\Deg=\dfrac{1}{2}\Cdota8\Cdota5\sin60\Deg \\[4pt]
&13\mathrm{AD}=40\sqrt{3} \\[4pt]
&\mathrm{AD}=\dfrac{40}{13}\sqrt{3}
\end{align*}


次は内接円の半径を求める問題。これも三角形の面積を利用しよう。

$\sankaku{ABC}$ の面積を $S$ とし,$\sankaku{ABC}$ の内接円の半径を $r$ とするとき,
&{\color{blue}\sankaku{IBC}}+{\color{green}\sankaku{ICA}}+{\color{red}\sankaku{IAB}}=\sankaku{ABC} \\[4pt]
&\dfrac{1}{2}ar+\dfrac{1}{2}br+\dfrac{1}{2}cr=S \\[4pt]
&\dfrac{1}{2}(a+b+c)r=S \\[4pt]
&r=\dfrac{2S}{a+b+c}
\end{align*}

この結果を覚えてしまっている人もいる。
&\dfrac{1}{2}(5+7+8)r=10\sqrt{3} \\[4pt]
&r=\sqrt{3}
\end{align*}

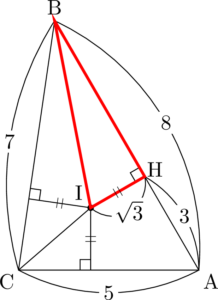
次はAHの長さを求めよう。直前にIHの長さも求めているから,$\sankaku{AHI}$ に着目しよう。今回は $\kaku{IAB}=30\Deg$ と分かっているから,すぐ求められるね。
\mathrm{AH}=\sqrt{3}\,\mathrm{IH}=3
\end{align*}


次のポイントも覚えておこう。
$\sankaku{ABC}$ の内接円と3辺AB, BC, CAとの接点をそれぞれP, Q, Rとする。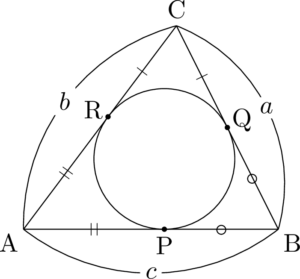
ここで,$\mathrm{AP=AR},~$$\mathrm{BP=BQ},~$$\mathrm{CQ=CR}$ であるから
&\mathrm{AP=AR}=\dfrac{b+c-a}{2} \\
&\mathrm{BP=BQ}=\dfrac{c+a-b}{2} \\
&\mathrm{CQ=CR}=\dfrac{a+b-c}{2}
\end{align*}

僕はこれをもう覚えてしまっているけど,導出できるなら別に覚えなくても良い。
AHは $\kaku{BAC}$ をはさむ接線の長さだから
\mathrm{AH}=\dfrac{5+8-7}{2}=3
\end{align*}

最後のBIの長さを求めよう。IHの長さが分かっているから $\sankaku{BHI}$ に着目しよう。
\mathrm{BH}=8-3=5
\end{align*}
\mathrm{BI}&=\sqrt{(\sqrt{3})^2+5^2} \\[4pt]
&=\sqrt{28} \\[4pt]
&=2\sqrt{7}
\end{align*}
まとめ

$\sin$ の値を利用して図を描くときは,鋭角と鈍角の2種類あることに注意しよう。ほとんどの場合,追加条件によって一方に定まるか,一方を指定されて問題が出題されるかである。



















