2020年センター試験 数学ⅠA 第2問 三角比の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2020年 センターⅠA 第2問 三角比$\sankaku{ABC}$ において,$\mathrm{BC}=2\sqrt{2}$ とする。$\kaku{ACB}$ の二等分線と辺ABの交点をDとし,$\mathrm{CD}=\sqrt{2}$, $\cos\kaku{BCD}=\dfrac{3}{4}$ とする。このとき,$\mathrm{BD}=\myBox{ア}$ であり
\begin{align*}
\sin\kaku{ADC}=\dfrac{\sqrt{\myBox{イウ}}}{\myBox{エ}}
\end{align*}
である。$\dfrac{\mathrm{AC}}{\mathrm{AD}}=\sqrt{\myBox{オ}}$ であるから\sin\kaku{ADC}=\dfrac{\sqrt{\myBox{イウ}}}{\myBox{エ}}
\end{align*}
\begin{align*}
\mathrm{AD}=\myBox{カ}
\end{align*}
である。また,$\sankaku{ABC}$ の外接円の半径は $\dfrac{\myBox{キ}\sqrt{\myBox{ク}}}{\myBox{ケ}}$ である。\mathrm{AD}=\myBox{カ}
\end{align*}
考え方と解答

ヒロ
BDの長さを求めるからBDを含む三角形を考えよう。

ヒロ
CDの長さと $\cos\kaku{BCD}$ の値が与えられているから $\sankaku{BCD}$ を考えよう。
【アの解答】
$\sankaku{BCD}$ において,余弦定理より
$\sankaku{BCD}$ において,余弦定理より
\begin{align*}
\mathrm{BD}^2&=\mathrm{BC}^2+\mathrm{CD}^2-2\mathrm{BC}\Cdota\mathrm{CD}\cos\kaku{BCD} \\[4pt]
&=(2\sqrt{2})^2+(\sqrt{2})^2-2\Cdota2\sqrt{2}\Cdota\sqrt{2}\Cdota\dfrac{3}{4} \\[4pt]
&=8+2-6 \\[4pt]
&=4
\end{align*}
$\mathrm{BD}>0$ より $\mathrm{BD}=2$\mathrm{BD}^2&=\mathrm{BC}^2+\mathrm{CD}^2-2\mathrm{BC}\Cdota\mathrm{CD}\cos\kaku{BCD} \\[4pt]
&=(2\sqrt{2})^2+(\sqrt{2})^2-2\Cdota2\sqrt{2}\Cdota\sqrt{2}\Cdota\dfrac{3}{4} \\[4pt]
&=8+2-6 \\[4pt]
&=4
\end{align*}

ヒロ
図を描いて状況を把握しよう。
【状況を把握する図】
点Aの位置は線分BDを点Dの方向へ延長した部分にあることが分かるが,正確な位置は分からないから適当に描いておく。
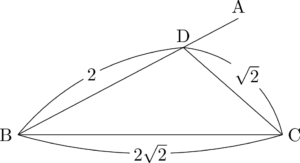
$\sin\kaku{ADC}$ は $\sin\kaku{BDC}$ と等しいことが分かる。
【イ~エの解答】
$\cos\kaku{BCD}=\dfrac{3}{4}$ より
$\cos\kaku{BCD}=\dfrac{3}{4}$ より
\begin{align*}
\sin\kaku{BCD}&=\sqrt{1-\left(\dfrac{3}{4}\right)^2} \\[4pt]
&=\dfrac{\sqrt{7}}{4}
\end{align*}
であるから,$\sankaku{BCD}$ において正弦定理より\sin\kaku{BCD}&=\sqrt{1-\left(\dfrac{3}{4}\right)^2} \\[4pt]
&=\dfrac{\sqrt{7}}{4}
\end{align*}
\begin{align*}
\dfrac{\sin\kaku{BDC}}{2\sqrt{2}}&=\dfrac{\sin\kaku{BCD}}{2} \\[4pt]
\sin\kaku{BDC}&=\sqrt{2}\Cdota\dfrac{\sqrt{7}}{4} \\[4pt]
&=\dfrac{\sqrt{14}}{4}
\end{align*}
よって,$\sin\kaku{ADC}=\dfrac{\sqrt{14}}{4}$\dfrac{\sin\kaku{BDC}}{2\sqrt{2}}&=\dfrac{\sin\kaku{BCD}}{2} \\[4pt]
\sin\kaku{BDC}&=\sqrt{2}\Cdota\dfrac{\sqrt{7}}{4} \\[4pt]
&=\dfrac{\sqrt{14}}{4}
\end{align*}

ヒロ
次は2辺ACとADの長さの比を求める問題。$\sankaku{ACD}$ に着目して考えよう。
【オの解答】
$\sankaku{ACD}$ において正弦定理より
$\sankaku{ACD}$ において正弦定理より
\begin{align*}
&\dfrac{\mathrm{AC}}{\sin\kaku{ADC}}=\dfrac{\mathrm{AD}}{\sin\kaku{ACD}} \\[4pt]
&\dfrac{\mathrm{AC}}{\mathrm{AD}}=\dfrac{\sin\kaku{ADC}}{\sin\kaku{ACD}}
\end{align*}
$\kaku{ACD}=\kaku{BCD}$ より&\dfrac{\mathrm{AC}}{\sin\kaku{ADC}}=\dfrac{\mathrm{AD}}{\sin\kaku{ACD}} \\[4pt]
&\dfrac{\mathrm{AC}}{\mathrm{AD}}=\dfrac{\sin\kaku{ADC}}{\sin\kaku{ACD}}
\end{align*}
\begin{align*}
\sin\kaku{ACD}=\sin\kaku{BCD}=\dfrac{\sqrt{7}}{4}
\end{align*}
であるから\sin\kaku{ACD}=\sin\kaku{BCD}=\dfrac{\sqrt{7}}{4}
\end{align*}
\begin{align*}
\dfrac{\mathrm{AC}}{\mathrm{AD}}&=\dfrac{\sqrt{14}}{4}\Cdota\dfrac{4}{\sqrt{7}} \\[4pt]
&=\sqrt{2}
\end{align*}
\dfrac{\mathrm{AC}}{\mathrm{AD}}&=\dfrac{\sqrt{14}}{4}\Cdota\dfrac{4}{\sqrt{7}} \\[4pt]
&=\sqrt{2}
\end{align*}

ヒロ
$\sankaku{ADC}$ に着目してADの長さを求めよう。
【カの解答】
$\sin\kaku{ADC}=\dfrac{\sqrt{14}}{4}$ より
よって,$\mathrm{AD}=1$
$\sin\kaku{ADC}=\dfrac{\sqrt{14}}{4}$ より
\begin{align*}
\cos\kaku{ADC}&=\sqrt{1-\sin^2\kaku{ADC}} \\[4pt]
&=\sqrt{1-\left(\dfrac{\sqrt{14}}{4}\right)^2} \\[4pt]
&=\dfrac{\sqrt{2}}{4}
\end{align*}
$\mathrm{AD}=x$ とすると,$\sankaku{ACD}$ において余弦定理より\cos\kaku{ADC}&=\sqrt{1-\sin^2\kaku{ADC}} \\[4pt]
&=\sqrt{1-\left(\dfrac{\sqrt{14}}{4}\right)^2} \\[4pt]
&=\dfrac{\sqrt{2}}{4}
\end{align*}
\begin{align*}
&(\sqrt{2}x)^2=x^2+(\sqrt{2})^2-2\sqrt{2}x\Cdota\dfrac{\sqrt{2}}{4} \\[4pt]
&2x^2=x^2+2-x \\[4pt]
&x^2+x-2=0 \\[4pt]
&(x+2)(x-1)=0 \\[4pt]
&x=-2,~1
\end{align*}
$x>0$ より,$x=1$&(\sqrt{2}x)^2=x^2+(\sqrt{2})^2-2\sqrt{2}x\Cdota\dfrac{\sqrt{2}}{4} \\[4pt]
&2x^2=x^2+2-x \\[4pt]
&x^2+x-2=0 \\[4pt]
&(x+2)(x-1)=0 \\[4pt]
&x=-2,~1
\end{align*}
よって,$\mathrm{AD}=1$

ヒロ
外接円の半径を求める場合は正弦定理で求めよう。
【キの解答】
$\mathrm{AC}=\sqrt{2}$ より,$\sankaku{ACD}$ は二等辺三角形であることが分かる。
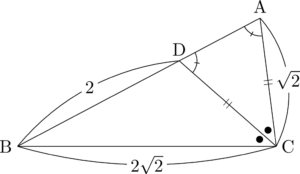
このとき $\kaku{BAC}=\kaku{ADC}$ だから
$\mathrm{AC}=\sqrt{2}$ より,$\sankaku{ACD}$ は二等辺三角形であることが分かる。

このとき $\kaku{BAC}=\kaku{ADC}$ だから
\begin{align*}
\sin A=\sin\kaku{ADC}=\dfrac{\sqrt{14}}{4}
\end{align*}
よって,正弦定理より\sin A=\sin\kaku{ADC}=\dfrac{\sqrt{14}}{4}
\end{align*}
\begin{align*}
R&=\dfrac{\mathrm{BC}}{2\sin A} \\[4pt]
&=\dfrac{2\sqrt{2}}{2}\Cdota\dfrac{4}{\sqrt{14}} \\[4pt]
&=\dfrac{4}{\sqrt{7}} \\[4pt]
&=\dfrac{4\sqrt{7}}{7}
\end{align*}
R&=\dfrac{\mathrm{BC}}{2\sin A} \\[4pt]
&=\dfrac{2\sqrt{2}}{2}\Cdota\dfrac{4}{\sqrt{14}} \\[4pt]
&=\dfrac{4}{\sqrt{7}} \\[4pt]
&=\dfrac{4\sqrt{7}}{7}
\end{align*}
別の考え方と解法

ヒロ
角の二等分線の性質を利用して次のようにして解いても良い。
【オの解答】
CDが $\kaku{ACB}$ の二等分線であるから
CDが $\kaku{ACB}$ の二等分線であるから
\begin{align*}
&\mathrm{AD}:\mathrm{BD}=\mathrm{AC}:\mathrm{BC} \\[4pt]
&\mathrm{AD}:2=\mathrm{AC}:2\sqrt{2} \\[4pt]
&2\sqrt{2}\mathrm{AD}=2\mathrm{AC} \\[4pt]
&\dfrac{\mathrm{AC}}{\mathrm{AD}}=\sqrt{2}
\end{align*}
&\mathrm{AD}:\mathrm{BD}=\mathrm{AC}:\mathrm{BC} \\[4pt]
&\mathrm{AD}:2=\mathrm{AC}:2\sqrt{2} \\[4pt]
&2\sqrt{2}\mathrm{AD}=2\mathrm{AC} \\[4pt]
&\dfrac{\mathrm{AC}}{\mathrm{AD}}=\sqrt{2}
\end{align*}

ヒロ
ADの長さを求める際に,別の角に着目して余弦定理を利用した場合は次のようになる。
【カの解答】
$\mathrm{AD}=x$ とすると,$\sankaku{ACD}$ において余弦定理より
$\sankaku{ABC}$ は直角二等辺三角形となる。このとき $\kaku{BCD}=45\Deg$ となるため,
$\cos\kaku{BCD}=\dfrac{3}{4}$ を満たさないから不適。
よって,$\mathrm{AD}=1$
$\mathrm{AD}=x$ とすると,$\sankaku{ACD}$ において余弦定理より
\begin{align*}
&x^2=(\sqrt{2}x)^2+(\sqrt{2})^2-2\sqrt{2}\Cdota\sqrt{2}x\Cdota\dfrac{3}{4} \\[4pt]
&x^2=2x^2+2-3x \\[4pt]
&x^2-3x+2=0 \\[4pt]
&(x-1)(x-2)=0 \\[4pt]
&x=1,~2
\end{align*}
$\mathrm{AD}=2$ のとき,$\mathrm{AC}=2\sqrt{2}$ となり,&x^2=(\sqrt{2}x)^2+(\sqrt{2})^2-2\sqrt{2}\Cdota\sqrt{2}x\Cdota\dfrac{3}{4} \\[4pt]
&x^2=2x^2+2-3x \\[4pt]
&x^2-3x+2=0 \\[4pt]
&(x-1)(x-2)=0 \\[4pt]
&x=1,~2
\end{align*}
$\sankaku{ABC}$ は直角二等辺三角形となる。このとき $\kaku{BCD}=45\Deg$ となるため,
$\cos\kaku{BCD}=\dfrac{3}{4}$ を満たさないから不適。
よって,$\mathrm{AD}=1$

ヒロ
$\sin\kaku{ACB}$ を求めるために,2倍角の公式を利用すると次のようになる。
【キ~ケの解答】
\begin{align*}
\sin\kaku{ACB}&=2\sin\kaku{BCD}\cos\kaku{BCD} \\[4pt]
&=2\Cdota\dfrac{\sqrt{7}}{4}\Cdota\dfrac{3}{4} \\[4pt]
&=\dfrac{3\sqrt{7}}{8}
\end{align*}
求める半径を $R$ とすると,正弦定理より\sin\kaku{ACB}&=2\sin\kaku{BCD}\cos\kaku{BCD} \\[4pt]
&=2\Cdota\dfrac{\sqrt{7}}{4}\Cdota\dfrac{3}{4} \\[4pt]
&=\dfrac{3\sqrt{7}}{8}
\end{align*}
\begin{align*}
R&=\dfrac{\mathrm{AB}}{2\sin\kaku{ACB}} \\[4pt]
&=3\Cdota\dfrac{4}{3\sqrt{7}} \\[4pt]
&=\dfrac{4\sqrt{7}}{7}
\end{align*}
R&=\dfrac{\mathrm{AB}}{2\sin\kaku{ACB}} \\[4pt]
&=3\Cdota\dfrac{4}{3\sqrt{7}} \\[4pt]
&=\dfrac{4\sqrt{7}}{7}
\end{align*}
2020年 センター数学ⅠA 三角比を解いた感想

ヒロ
問題文があっさりしているが,意外と面倒である。

ヒロ
誘導の意図が分からなくても,三角関数の2倍角の公式を利用することで解くこともできる。

ヒロ
誘導通りに解けるような実力を身に付けることが重要である。




















