場合の数・確率に関して漸化式を利用して解くときに,最初や最後に着目するだけでは解けないような問題を説明します。
問題で扱われている複数の状態が回数や時間によって次々と変化していく場合には「状態遷移図」を描くことで考えやすくなります。
ここでは2018年に大阪大学で出題された入試問題を例として解説します。
2018年 大阪大

それでは次の問題を解いてみよう。
(1)の考え方と解答

この問題では,試合ごとに勝率が変化する点が厄介だね。

そうなんですよ。それで困ってます。

$n$ 試合目にAが勝つ確率は,その1つ前の $n-1$ 試合目にAとBのどちらが勝ったかによって変わってくるね。

でもその $n-1$ 試合目の勝率も,その前の $n-2$ 試合目の影響を受ける。

だから「こんなの解けるはずがない」と思ってしまいます。

具体的に3試合目にAが勝つ確率を求めよと言われている問題なら,1試合目から順番に考えることで求めることもできるけど,$n$ 試合目という文字が出てきてるから,この考え方もできない。

このように試合ごとに各自の勝率が変化する問題では「状態遷移図」を描いて状況を整理しよう。

状態遷移図って何ですか?
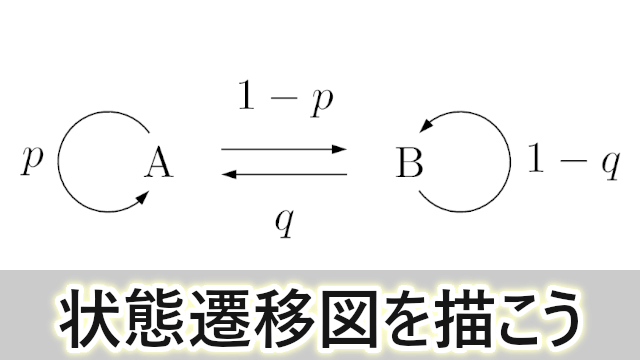
状態遷移図とは何かを簡単に説明しておくと,状態から状態への移り変わりの様子を表した図のことで,今回の問題で状態遷移図を描くと次のようになる。
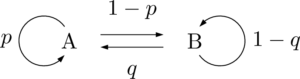
この図で「A」はAが勝つ状態を表していて「B」はBが勝つ状態を表している。
ある試合でAが勝った場合,次の試合でAが勝つ確率が $p$ だから,AからAへの矢印を描いてその変化の確率が $p$ であることが分かるように $p$ と書いておく。
また,引き分けはないため,Aが勝った試合の次の試合でBが勝つ確率は $1-p$ であるから,AからBへ向かう矢印を描いてその確率 $1-p$ を書く。
ある試合でBが勝った場合も同様にして矢印と確率を描くと上の状態遷移図が完成する。

この状態遷移図を描いておけば,「どういう設定だったっけ?」てならなくて済みますね。

次に,状態遷移図を利用した考え方について説明するよ。
状態遷移図を利用して,2試合目にAが勝つ確率を求める場合は,最初にAに向かう矢印を探そう。
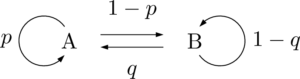
AからAに向かう矢印とBからAに向かう矢印の2本の矢印を見つけることができる。
AからAに向かう矢印には $p$ と書かれていて,BからAに向かう矢印には $q$ と書かれている。
着目している部分を赤色にすると次のようになる。

状態遷移図より,2試合目にAが勝つ確率は
(1試合目に\mathrm{A}が勝つ確率)\times p+(1試合目に\mathrm{B}が勝つ確率)\times q
\end{align*}
同様に考えることで,3試合目にAが勝つ確率は
(2試合目に\mathrm{A}が勝つ確率)\times p+(2試合目に\mathrm{B}が勝つ確率)\times q
\end{align*}
また,Bが勝つ確率を求めたい場合は,Bに向かう矢印に着目することで同様に求めることができる。

これは便利ですね!

状態遷移図を描いた後は,漸化式を立式していこう。

そして漸化式を立式できれば大丈夫だというくらい,漸化式を解く力を付けておくことも重要だね。

このように自分で漸化式を立式して解いていく問題では,当然だが誘導はないため,自力で漸化式を解ききる数学力が必要となる。

誘導なしで漸化式を解くのが苦手な人は,様々なタイプの漸化式について自力で解く練習をしておこう。
$n+1$ 試合目にAが勝つのは,$n$ 試合目にAが勝って,$n+1$ 試合目にAが勝つ場合と,$n$ 試合目にBが勝って,$n+1$ 試合目にAが勝つ場合があるから,
a_{n+1}&=a_n\Cdota p+(1-a_n)\Cdota q \\[4pt]
&=(p-q)a_n+q
\end{align*}
条件より $1-p+q\neq0$ であるから,$\alpha=\dfrac{q}{1-p+q}$とおくと,
a_{n+1}-\alpha=(p-q)(a_n-\alpha)
\end{align*}
a_n-\alpha=(a_1-\alpha)(p-q)^{n-1}
\end{align*}
a_1-\alpha&=p-\dfrac{q}{1-p+q} \\
&=\dfrac{p(1-p+q)-q}{1-p+q} \\
&=\dfrac{p(1-p)-q(1-p)}{1-p+q} \\
&=\dfrac{(p-q)(1-p)}{1-p+q}
\end{align*}
a_n=\dfrac{(1-p)(p-q)^n+q}{1-p+q}
\end{align*}
(2)の考え方と解答
(2) $n\geqq3$ とする。Bが連勝せずにちょうど2試合に勝つ確率 $b_n$ を求めよ。

「Bが連勝しない」という部分をどのように考えるかがポイントとなるね。

状態遷移図だけで解くのは無理な気がします。

ということで,試合に勝ったチームを書き並べる方法で考えよう。
例えば5試合のうち,Bが連勝せずに2試合に勝つ確率を考えよう。
AABAB,BAAAB,ABABA,BABAAの4つの場合を考える。
- AABABの場合は $\mathrm{A\to A}$ が1回,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が1回起こる。
- BAAABの場合は $\mathrm{A\to A}$ が2回,$\mathrm{A\to B}$ が1回,$\mathrm{B\to A}$ が1回起こる。
- ABABAの場合は $\mathrm{A\to A}$ が0回,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が2回起こる。
- BABAAの場合は $\mathrm{A\to A}$ が1回,$\mathrm{A\to B}$ が1回,$\mathrm{B\to A}$ が2回起こる。

4つの例で分かったことは,最初と最後の試合でAが勝つかBが勝つかで大きく分かれることが分かる。

4パターンで場合分けするのは面倒なんですけど・・・

そうだね。すべてを場合分けして考えるのは面倒なので,少し工夫することを考えよう。
1試合目にA,Bが勝つ確率はそれぞれ $p,~1-p$ であるため,1試合目にAが勝つ場合を $\mathrm{A\to A}$ が1回起こったとし,1試合目にBが勝つ場合を $\mathrm{A\to B}$ が1回起こったと考えても同じことだと分かる。
この工夫でさっきの4つの例がどうなるかを確認すると次のようになる。
- AABABの場合は $\mathrm{A\to A}$ が2回,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が1回起こる。
- BAAABの場合は $\mathrm{A\to A}$ が2回,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が1回起こる。
- ABABAの場合は $\mathrm{A\to A}$ が1回,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が2回起こる。
- BABAAの場合は $\mathrm{A\to A}$ が1回,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が2回起こる。

これで1試合目に勝つチームの違いによって回数の違いがなくなったため,最後の試合でどちらが勝つかで場合分けすればよいことが分かる。

しかも回数の合計も5になって,試合数と一致するから $n$ 試合という試合数が文字になっても考えやすくなりますね。

これで解答を書くことができるね。
勝ったチーム名を左から順に $n$ 個並べて $n$ 試合の勝敗を表すことにする。
ある試合でA,~Bが勝つ確率は右図のように決められており,1試合目にA,~Bが勝つ確率がそれぞれ $p,~1-p$ であることから,1試合目にAが勝つ場合を $\mathrm{A\to A}$ が1回起こったとし,1試合目にBが勝つ場合を $\mathrm{A\to B}$ が1回起こったとしてもよい。
(i) $n$ 試合目にAが勝つ場合
Aを $n-2$ 個並べ,左端と間の $n-2$ か所から2か所選んでBを入れればよい。
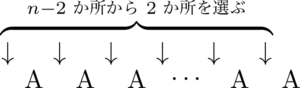
このとき,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が2回,$\mathrm{A\to A}$ が $n-4$ 回起こるから,その確率は
\nCk{n-2}{2}(1-p)^2q^2p^{n-4}
\end{align*}
Aを$n-2$個,Bを右端に1個並べて,右図のように左端と間の$n-2$か所から1か所選んでBを入れればよい。
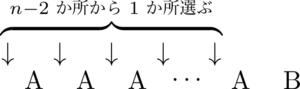
このとき,$\mathrm{A\to B}$ が2回,$\mathrm{B\to A}$ が1回,$\mathrm{A\to A}$ が $n-3$ 回起こるから,その確率は
(n-2)(1-p)^2qp^{n-3}
\end{align*}
b_n&=\nCk{n-2}{2}(1-p)^2q^2p^{n-4}+(n-2)(1-p)^2qp^{n-3} \\
&=\dfrac12(n-2)(1-p)^2qp^{n-4}\{(n-3)q+2p\} \\
&=\dfrac12(n-2)(1-p)^2qp^{n-4}(nq+2p-3q)
\end{align*}