2018年センター試験 数学ⅡB 第2問微積の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
(1) $q$ と $r$ を,$p$ を用いて表そう。放物線 $C$ 上の点Aにおける接する $\ell$ の傾きは $\myBox{ア}$ であることから,$q=\myBox{イウ}~p+\myBox{エ}$ がわかる。さらに,$C$ は点Aを通ることから,$r=p-\myBox{オ}$ となる。
(2) $v>1$ とする。放物線 $C$ と直線 $\ell$ および直線 $x=v$ で囲まれた図形の面積 $S$ は
S=\dfrac{p}{\myBox{カ}}\left(v^3-\myBox{キ}~v^2+\myBox{ク}~v-\myBox{ケ}\right)
\end{align*}
$U=S-T$ は $v=2$ で極値をとるとする。このとき,$p=\myBox{サ}$ であり,$v>1$ の範囲で $U=0$ となる $v$ の値を $v_0$ とすると,$v_0=\dfrac{\myBox{シ}+\sqrt{\myBox{ス}}}{\myBox{セ}}$ である。$1<v<v_0$ の範囲で $U$ は $\myBox{ソ}$。$\myBox{ソ}$ に当てはまるものを,次の⓪~④のうちから一つ選べ。
⓪ つねに増加する ① つねに減少する ② 正の値のみをとる
③ 負の値のみをとる ④ 正と負のどちらの値もとる
$p=\mybox{サ}$ のとき,$v>1$ における $U$ の最小値は $\myBox{タチ}$ である。
〔2〕関数 $f(x)$ は $x\geqq1$ の範囲でつねに $f(x)\leqq0$ を満たすとする。$t>1$ のとき,曲線 $y=f(x)$ と $x$ 軸および2直線 $x=1,~x=t$ で囲まれた図形の面積を $W$ とする。$t$ が $t>1$ の範囲を動くとき,$W$ は,底辺の長さが $2t^2-2$,他の2辺の長さがそれぞれ $t^2+1$ の二等辺三角形の面積とつねに等しいとする。このとき,$x>1$ における $f(x)$ を求めよう。
$F(x)$ を $f(x)$ の不定積分とする。一般に,$F'(x)=\myBox{ツ}$, $W=\myBox{テ}$ が成り立つ。$\myBox{ツ}$,$\myBox{テ}$ に当てはまるものを,次の⓪~⑧のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $-F(t)$ ① $F(t)$ ② $F(t)-F(1)$
③ $F(t)+F(1)$ ④ $-F(t)+F(1)$ ⑤ $-F(t)-F(1)$
⑥ $-f(x)$ ⑦ $f(x)$ ⑧ $f(x)-f(1)$
したがって,$t>1$ において
f(t)=\myBox{トナ}~t^{~\myBox{ニ}}+\myBox{ヌ}
\end{align*}
〔1〕(1)の考え方と解答

直線の傾きの理解度を確認する問題。これができなければ中2からやり直そう。
$\ell:y=2x-1$ だから,$\ell$ の傾きは2である。

次は点Aにおける接線の傾きを求める問題。つまり,微分係数を求める問題。
$y=px^2+qx+r$ より,$y’=2px+q$
$x=1$ のとき,$y’=2$ となるから
&2p+q=2 \\[4pt]
&q=-2p+2
\end{align*}

点Aが $C$ 上にあるとき何がいえるか考えよう。

求めるのは $r$ と $p$ の関係式だから,直前に求めた $q$ を $p$ で表している式を利用することが分かる。そこまで読めなかったとしても「さらに」の言葉で分かるようになろう。
点 $\mathrm{A}(1,~1)$ が $C$ 上にあるから
&p+q+r=1 \\[4pt]
&p+(-2p+2)+r=1 \\[4pt]
&r=p-1
\end{align*}
〔1〕(2)の考え方と解答
(2) $v>1$ とする。放物線 $C$ と直線 $\ell$ および直線 $x=v$ で囲まれた図形の面積 $S$ は
\begin{align*}である。また,$x$ 軸と $\ell$ および2直線 $x=1,~x=v$ で囲まれた図形の面積 $T$ は,$T=v^{~\myBox{コ}}-v$ である。
S=\dfrac{p}{\myBox{カ}}\left(v^3-\myBox{キ}~v^2+\myBox{ク}~v-\myBox{ケ}\right)
\end{align*}
$U=S-T$ は $v=2$ で極値をとるとする。このとき,$p=\myBox{サ}$ であり,$v>1$ の範囲で $U=0$ となる $v$ の値を $v_0$ とすると,$v_0=\dfrac{\myBox{シ}+\sqrt{\myBox{ス}}}{\myBox{セ}}$ である。$1<v<v_0$ の範囲で $U$ は $\myBox{ソ}$。$\myBox{ソ}$ に当てはまるものを,次の⓪~④のうちから一つ選べ。
⓪ つねに増加する ① つねに減少する ② 正の値のみをとる
③ 負の値のみをとる ④ 正と負のどちらの値もとる
$p=\mybox{サ}$ のとき,$v>1$ における $U$ の最小値は $\myBox{タチ}$ である。

放物線と接線と $y$ 軸に平行な直線で囲まれる図形の面積を求める問題だから,3分の1公式を利用しよう。

グラフを描かず,定積分の式も書かずに求められるようになろう。
S&=\dfrac{p}{3}(v-1)^3 \\[4pt]
&=\dfrac{p}{3}(v^3-3v^2+3v-1)
\end{align*}
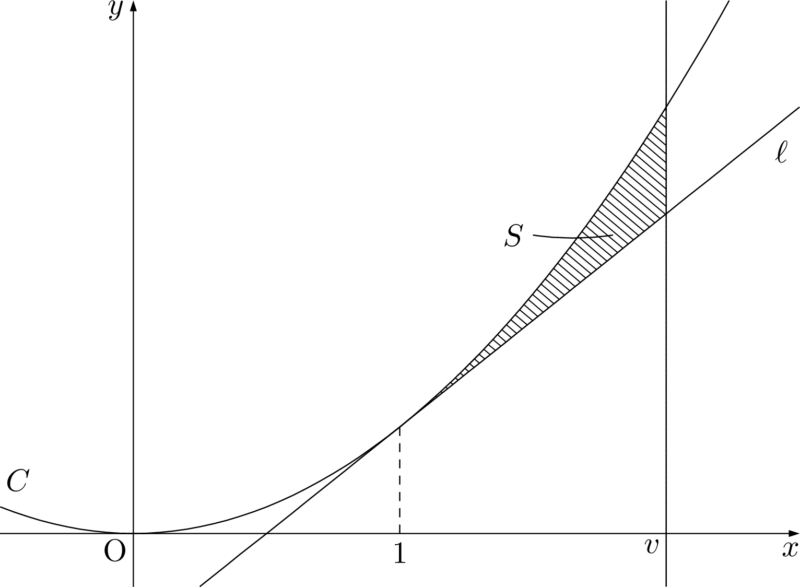

次の面積 $T$ は台形の面積。ちなみに空欄を埋めることだけを考えるなら,$v$ の何次式かを考えれば良いから,答えは2と分かる。
T&=\dfrac{1+(2v-1)}{2}(v-1) \\[4pt]
&=v^2-v
\end{align*}

$U$ を $v$ の関数とみて,$v=2$ で極値をとるという条件から $p$ の値を求める問題。展開前の式のまま微分できると書く量を減らすことができる。
$U=\dfrac{p}{3}(v-1)^3-(v^2-v)$ より
\dfrac{dU}{dv}&=p(v-1)^2-(2v-1)
\end{align*}
&p-3=0 \\[4pt]
&p=3
\end{align*}

次は $U=0$ の解を求める問題。
$U=0$ より
&(v-1)^3-(v^2-v)=0 \\[4pt]
&(v-1)\{(v-1)^2-v\}=0 \\[4pt]
&(v-1)(v^2-3v+1)=0
\end{align*}
&v^2-3v+1=0 \\[4pt]
&v=\dfrac{3\pm\sqrt{5}}{2}
\end{align*}
v_0=\dfrac{3+\sqrt{5}}{2}
\end{align*}

次は $U$ の符号を考える問題。
$U=(v-1)(v^2-3v+1)$ より,$1<v<v_0$ における $U$ の符号は $v^2-3v+1$ の符号と一致する。$y=v^2-3v+1$ のグラフは次のようになる。

よって,$1<v<v_0$ の範囲で $U$ は負の値のみをとる。$\myBox{ソ}=③$

次は $U$ の最小値を求める問題。
さっきの図に $y=v-1$ のグラフを描き加えると,次のようになる。

$U$ は $v-1$ と $v^2-3v+1$ の積だから,図の黒丸の3点を通ることが分かる。頭の中では次のような赤い曲線が見えている。想像では正確なグラフは分からないが,大体の感覚がつかめれば良い。ちなみに次の図では,$U$ のグラフを正確に描いている。
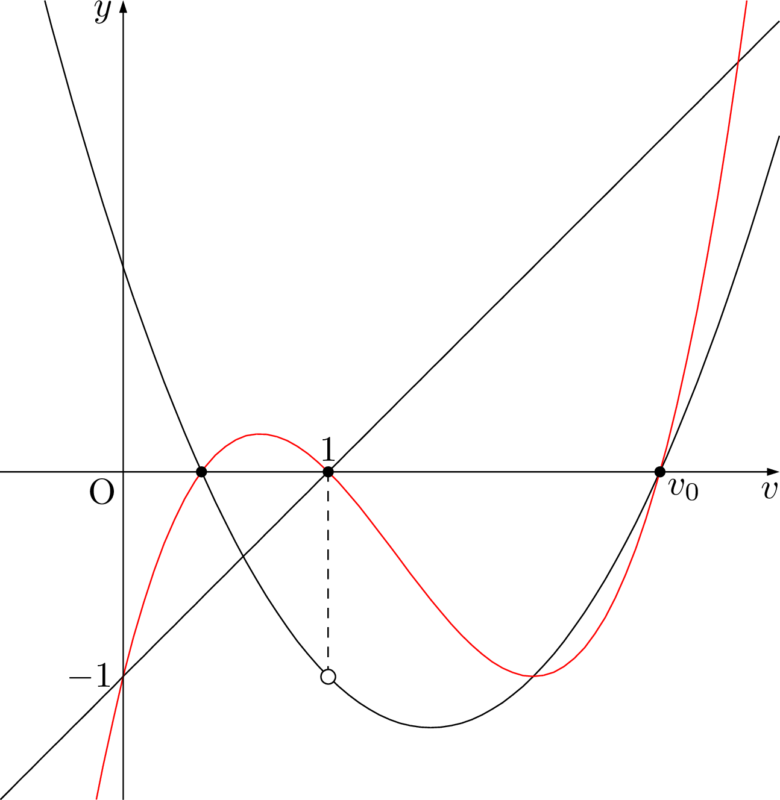
よって,$v>1$ における $U$ の最小値は極小値に等しい。$v=2$ で極値をとることが分かっているから,$v=2$ のとき,$U$ は最小値をとる。求める最小値は
(2-1)(2^2-3\Cdota2+1)=-1
\end{align*}
〔2〕の考え方と解答
〔2〕関数 $f(x)$ は $x\geqq1$ の範囲でつねに $f(x)\leqq0$ を満たすとする。$t>1$ のとき,曲線 $y=f(x)$ と $x$ 軸および2直線 $x=1,~x=t$ で囲まれた図形の面積を $W$ とする。$t$ が $t>1$ の範囲を動くとき,$W$ は,底辺の長さが $2t^2-2$,他の2辺の長さがそれぞれ $t^2+1$ の二等辺三角形の面積とつねに等しいとする。このとき,$x>1$ における $f(x)$ を求めよう。
$F(x)$ を $f(x)$ の不定積分とする。一般に,$F'(x)=\myBox{ツ}$, $W=\myBox{テ}$ が成り立つ。$\myBox{ツ}$,$\myBox{テ}$ に当てはまるものを,次の⓪~⑧のうちから一つずつ選べ。ただし,同じものを選んでもよい。
⓪ $-F(t)$ ① $F(t)$ ② $F(t)-F(1)$
③ $F(t)+F(1)$ ④ $-F(t)+F(1)$ ⑤ $-F(t)-F(1)$
⑥ $-f(x)$ ⑦ $f(x)$ ⑧ $f(x)-f(1)$
したがって,$t>1$ において\begin{align*}である。よって,$x>1$ における $f(x)$ がわかる。
f(t)=\myBox{トナ}~t^{~\myBox{ニ}}+\myBox{ヌ}
\end{align*}

$F(x)$ と $f(x)$ の関係を確かめる問題だね。
$F(x)$ が $f(x)$ の不定積分だから,
F'(x)=f(x)
\end{align*}

次の $W$ は定積分について理解できているかを確認する問題だね。
W&=\dint{1}{t}\{0-f(x)\}\;dx \\[4pt]
&=\tint{-F(x)}{1}{t} \\[4pt]
&=-F(t)+F(1)
\end{align*}

問題文に書かれている二等辺三角形の面積を求めて $W$ の式を確定させよう。
二等辺三角形は次の図のようになる。
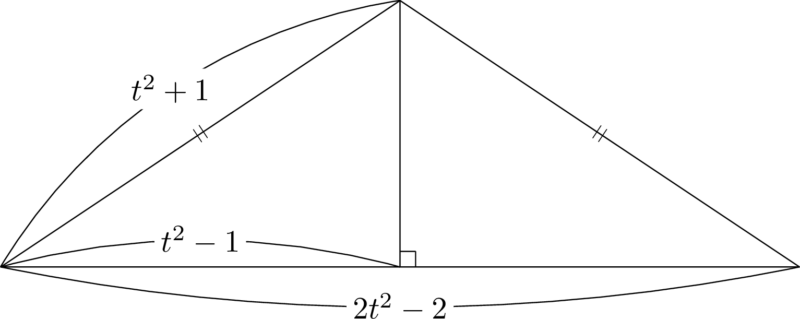
三角形の高さを $h$ とすると
h&=\sqrt{(t^2+1)^2-(t^2-1)^2} \\[4pt]
&=\sqrt{4t^2} \\[4pt]
&=2t
\end{align*}
W&=\dfrac{1}{2}(2t^2-2)\Cdota2t \\[4pt]
&=2t^3-2t
\end{align*}
f(t)&=F'(t) \\[4pt]
&=(F(1)-W)’ \\[4pt]
&=(-2t^3+2t)’ \\[4pt]
&=-6t^2+2
\end{align*}
2018年 センター数学ⅡB微積を解いた感想

2018年のセンター試験の数学では,マーク式ならではの解法を利用することで時間短縮できる問題が多くある。

(2)では3分の1公式を利用して面積を求めることができた。ただ,楽に求めることが出来る分だけ,展開しないといけないことがより面倒に感じる。

$U$ を微分するときは,$(x+a)^n$ の微分を利用できるようにしておきたい。

$U=0$ の解を求める問題では,展開前の式を利用することで,解の1つが $v=1$ であることが簡単に分かるため,因数分解が楽になる。

$U$ の最小値を求める問題では,通常なら,増減を調べるために,展開しないといけないと考える。しかし,今回は与えられている範囲と極値をとる $v$ の値が絶妙にマッチしていたため,簡単に求めることができた。

〔2〕の $W$ を定積分で求めるときには,$x$ 軸との上下関係を考えていない人は間違えるだろう。$W$ を間違えた場合,最後の $f(t)$ の空欄部分が合わないため,それで気付いた人もいるかもしれない。




















