2016年のセンター試験 数学ⅡB 第4問ベクトルの解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
(1) $0\leqq s\leqq1,~0\leqq t\leqq1$ であるような実数 $s,~t$ を用いて $\Vec{OP}=s\vec{a}$, $\Vec{OQ}=(1-t)\vec{b}+t\vec{c}$ と表す。$\vec{a}\Cdot\vec{b}=\vec{a}\Cdot\vec{c}=\myBox{ア},~\vec{b}\Cdot\vec{c}=\myBox{イ}$ であることから
\abs{\Vec{PQ}}^2=\left(\myBox{ウ}s-\myBox{エ}\right)^2+\left(\myBox{オ}t-\myBox{カ}\right)^2+\myBox{キ}
\end{align*}
(2) 三角形ABCの重心をGとする。$\abs{\Vec{PQ}}=\sqrt{\mybox{シ}}$ のとき,三角形GPQの面積を求めよう。
$\Vec{OA}\Cdot\Vec{PQ}=\myBox{ス}$ から,$\kaku{APQ}=\myBox{セソ}\Deg$ である。したがって,三角形APQの面積は $\sqrt{\myBox{タ}}$ である。また
\Vec{OG}=\dfrac{\myBox{チ}}{\myBox{ツ}}\Vec{OA}+\dfrac{\myBox{テ}}{\myBox{ト}}\Vec{OQ}
\end{align*}
以上のことから,三角形GPQの面積は $\dfrac{\sqrt{\myBox{ニ}}}{\myBox{ヌ}}$ である。
(1)の解答

$\vec{a}$ と $\vec{b}$ の内積を求めたいから,三角形OABに着目しよう。
$\abs{\vec{a}}=3$, $\abs{\vec{b}}=2$, $\kaku{AOB}=60\Deg$ より
\vec{a}\Cdot\vec{b}&=\abs{\vec{a}}\abs{\vec{b}}\cos60\Deg \\[4pt]
&=3\Cdota2\Cdota\dfrac{1}{2} \\[4pt]
&=3
\end{align*}

$\vec{a}\Cdot\vec{c}$ については,問題文から $\vec{a}\Cdot\vec{b}$ と等しいことが分かるから特に求める必要がないので,時間が足りなくなる人は,等しくなることを確認しない方が速くなる。

次は $\vec{b}$ と $\vec{c}$ の内積を求めたいから,三角形OBCに着目しよう。
$\abs{\vec{b}}=2$, $\abs{\vec{c}}=2$, $\kaku{BOC}=60\Deg$ より
\vec{b}\Cdot\vec{c}&=\abs{\vec{b}}\abs{\vec{c}}\cos60\Deg \\[4pt]
&=2^2\Cdota\dfrac{1}{2} \\[4pt]
&=2
\end{align*}

$\Vec{PQ}$ の始点をOに変えて $\vec{a}$, $\vec{b}$, $\vec{c}$ で表して,ベクトルの大きさの2乗を計算しよう。
\Vec{PQ}&=\Vec{OQ}-\Vec{OP} \\[4pt]
&=-s\vec{a}+(1-t)\vec{b}+t\vec{c}
\end{align*}
\abs{\Vec{PQ}}^2&=\abs{-s\vec{a}+(1-t)\vec{b}+t\vec{c}}^2 \\[4pt]
&=s^2\abs{\vec{a}}^2+(1-t)^2\abs{\vec{b}}^2+t^2\abs{\vec{c}}^2-2s(1-t)\vec{a}\Cdot\vec{b}+2t(1-t)\vec{b}\Cdot\vec{c}-2st\vec{c}\Cdot\vec{a} \\[4pt]
&=9s^2+{\color{red}4(1-t)^2}+4t^2{\color{blue}-6s(1-t)}+{\color{red}4t(1-t)}{\color{blue}-6st} \\[4pt]
&=9s^2{\color{blue}-6s}+{\color{red}4(1-t)\{(1-t)+t\}}+4t^2 \\[4pt]
&=9s^2-6s+4t^2-4t+4 \\[4pt]
&=(3s-1)^2+(2t-1)^2+2
\end{align*}

$\abs{\Vec{PQ}}$ はベクトルの大きさで0以上だから,最小となるのは,$\abs{\Vec{PQ}}^2$ が最小となるときだね。

実数の2乗は0以上であることを利用して最小値を求めよう。
$\abs{\Vec{PQ}}$ が最小になるのは $\abs{\Vec{PQ}}^2$ が最小になるときであり,
\abs{\Vec{PQ}}^2=(3s-1)^2+(2t-1)^2+2
\end{align*}
3s-1=0~~かつ~~2t-1=0
\end{align*}
s=\dfrac{1}{3},~t=\dfrac{1}{2}
\end{align*}
\abs{\Vec{PQ}}=\sqrt{2}
\end{align*}
(2)の解答

問題文からは $\Vec{OA}$ と $\Vec{PQ}$ の内積の値から $\kaku{APQ}$ の大きさを求めることができることが分かる。

この書き方だと,内積は0でなす角は $90\Deg$ であることが予想できる。この時点で時間がなくなっている人は0と90にマークしておこう。

時間に余裕がある人は,答えを予想しながら念のため計算しよう。
$\abs{\Vec{PQ}}=\sqrt{2}$ のとき,$s=\dfrac{1}{3}$, $t=\dfrac{1}{2}$ であるから
\Vec{PQ}&=-\dfrac{1}{3}\vec{a}+\dfrac{1}{2}\vec{b}+\dfrac{1}{2}\vec{c}
\end{align*}
\Vec{OA}\Cdot\Vec{PQ}&=-\dfrac{1}{3}\abs{\vec{a}}^2+\dfrac{1}{2}\vec{a}\Cdot\vec{b}+\dfrac{1}{2}\vec{c}\Cdot\vec{a} \\[4pt]
&=-3+\dfrac{3}{2}+\dfrac{3}{2} \\[4pt]
&=0
\end{align*}

予想通りの答えだね。これで三角形APQは直角三角形だと分かった。面積を求めよう。

ここまで図を描かずに求めてきたけど,このあたりで図を描いておいても良い。
四面体OABCは次の図のようになる。
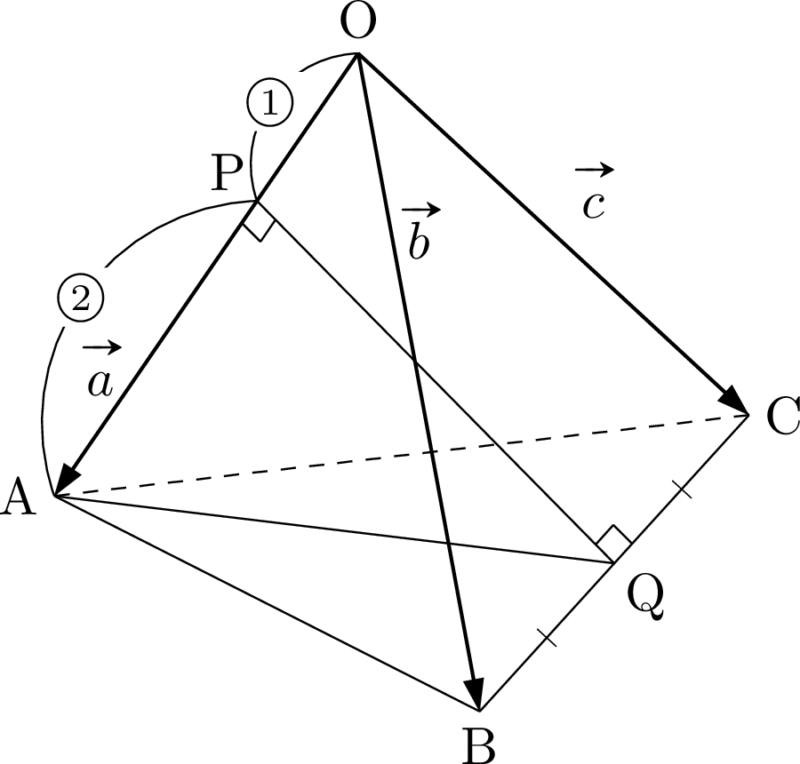
$\Vec{PA}=\dfrac{2}{3}\Vec{OA}$ より,$\abs{\Vec{PA}}=\dfrac{2}{3}\Cdot3=2$ であるから
\sankaku{APQ}&=\dfrac{1}{2}\abs{\Vec{PA}}\abs{\Vec{PQ}} \\[4pt]
&=\dfrac{1}{2}\Cdot2\Cdot\sqrt{2} \\[4pt]
&=\sqrt{2}
\end{align*}

次は $\Vec{OG}$ を求めよう。

Gは三角形ABCの重心ということを思い出そう。そして,重心は3本の中線の交点で,中線を $2:1$ に内分する性質があったね。

いまQがBCの中点だから,AQは中線になっている。つまり,AQを $2:1$ に内分する点がGということ。

先に $\myBox{ナ}$ が埋まったけど $\Vec{OG}$ を求めよう。
三角形ABCの重心Gは,次の図の位置にある。
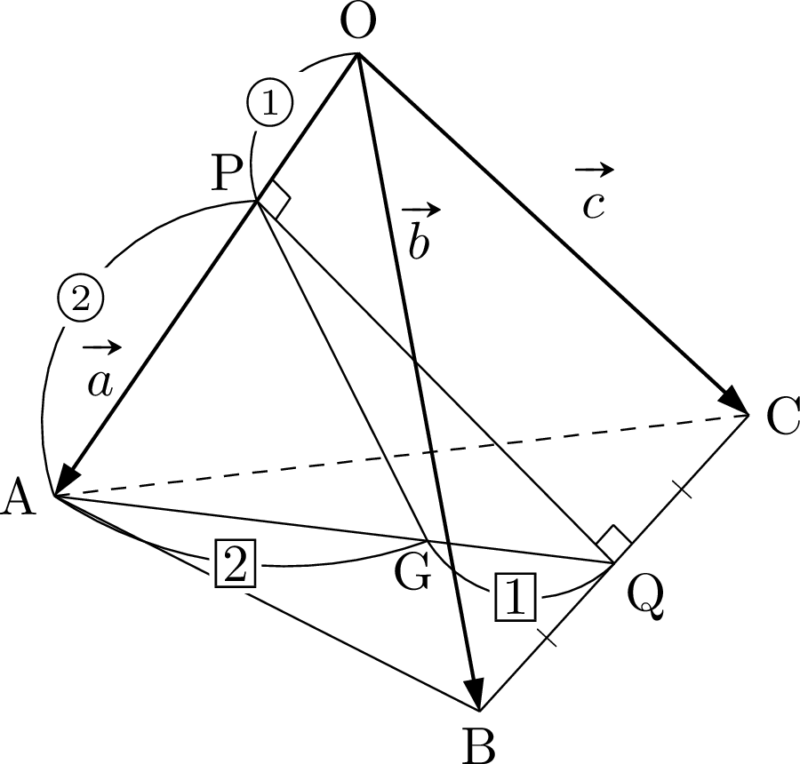
重心GはAQを $2:1$ に内分するから
\Vec{OG}=\dfrac{1}{3}\Vec{OA}+\dfrac{2}{3}\Vec{OQ}
\end{align*}

最後は三角形GPQの面積を求める問題。2回目の面積は比を利用して求めるのが基本。

今回の場合,三角形APQの面積が1回目の面積を求める問題になっているから,三角形APQと三角形GPQの2つの三角形に着目しよう。
$\mathrm{AG:GQ=2:1}$ より
\sankaku{GPQ}&=\dfrac{1}{3}\sankaku{APQ} \\[4pt]
&=\dfrac{\sqrt{2}}{3}
\end{align*}
2016年 センター数学ⅡB ベクトルを解いた感想
ベクトルの内積や大きさを求める問題では,どうなっているのか分からないとき以外は,図を描かずに求められるようになると良いだろう。
四面体をいつでも苦労せずに描けるようにした方が良い。できれば正八面体くらいは描けるようにしておこう。
正八面体を綺麗に描く1つの方法。 pic.twitter.com/gtCA9uuLzR
— ヒロ@大学入試数学の考え方と解法 (@_methodology) September 15, 2019




















