2016年センター試験 数学ⅠA 第5問 平面図形の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
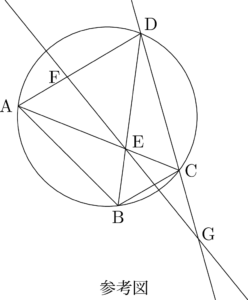
次の $\mybox{ア}$ には,下の⓪~④のうちから当てはまるものを一つ選べ。
$\kaku{ABC}$ の大きさが変化するとき四角形ABCDの外接円の大きさも変化することに注意すると,$\kaku{ABC}$ の大きさがいくらであっても,$\kaku{DAC}$ と大きさが等しい角は,$\kaku{DCA}$ と $\kaku{DBC}$ と $\myBox{ア}$ である。
⓪ $\kaku{ABD}$ ① $\kaku{ACB}$ ② $\kaku{ADB}$
③ $\kaku{BCG}$ ④ $\kaku{BEG}$
このことより $\dfrac{\mathrm{EC}}{\mathrm{AE}}=\dfrac{\myBox{イ}}{\myBox{ウ}}$ である。
次に,$\sankaku{ACD}$ と直線FEに着目すると,$\dfrac{\mathrm{GC}}{\mathrm{DG}}=\dfrac{\myBox{エ}}{\myBox{オ}}$ である。
(1) 直線ABが点Gを通る場合について考える。
このとき,$\sankaku{AGD}$ の辺AG上に点Bがあるので,$\mathrm{BG}=\myBox{カ}$ である。
また,直線ABと直線DCが点Gで交わり,4点A,B,C,Dは同一円周上にあるので,$\mathrm{DC}=\myBox{キ}\sqrt{\myBox{ク}}$ である。
(2) 四角形ABCDの外接円の直径が最小となる場合について考える。
このとき,四角形ABCDの外接円の直径は $\myBox{ケ}$ であり,$\kaku{BAC}=\myBox{コサ}\Deg$ である。
また,直線FEと直線ABの交点をHとするとき,$\dfrac{\mathrm{GC}}{\mathrm{DG}}=\dfrac{\mybox{エ}}{\mybox{オ}}$ の関係に着目してAHを求めると,$\mathrm{AH}=\myBox{シ}$ である。
ウォーミングアップ問題の解答

まずは $\kaku{DAC}$ と大きさが等しい角を探す問題。

$\kaku{DAC}$ と大きさが等しい角として,$\kaku{DCA}$ が書かれている。これは $\mathrm{DA=DC}$ より,$\sankaku{DAC}$ は二等辺三角形であるから「確かにそうだ」と納得できる。

また,$\kaku{DBC}$ は $\ko{\mathrm{CD}}$ に対する円周角に着目すると $\kaku{DAC}$ と等しい角であることが分かる。
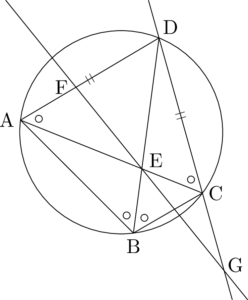

次は辺の長さの比の値を求める問題。問題文の「このことより」とあるから,$\kaku{DAC}$ と大きさが等しい角を考えるのは当然だね。
$\dfrac{\mathrm{EC}}{\mathrm{AE}}$ を求めるために,$\mathrm{EC}:\mathrm{AE}$ を考える。今回は $\kaku{ABD}=\kaku{DBC}$ であることを考えると,BEが $\kaku{ABC}$ の二等分線になっていることが分かるから
\mathrm{EC}:\mathrm{AE}&=\mathrm{BC}:\mathrm{AB} \\[4pt]
&=2:4 \\[4pt]
&=1:2
\end{align*}
\dfrac{\mathrm{EC}}{\mathrm{AE}}=\dfrac{1}{2}
\end{align*}

次は $\sankaku{ACD}$ と直線FEに着目して $\dfrac{\mathrm{GC}}{\mathrm{DG}}$ を求める問題。メネラウスの定理を使うことが分かるね。
メネラウスの定理より
&\dfrac{\mathrm{GC}}{\mathrm{DG}}\Cdota\dfrac{\mathrm{EA}}{\mathrm{CE}}\Cdota\dfrac{\mathrm{FD}}{\mathrm{AF}}=1 \\[4pt]
&\dfrac{\mathrm{GC}}{\mathrm{DG}}\Cdota\dfrac{2}{1}\Cdota\dfrac{3}{2}=1 \\[4pt]
&\dfrac{\mathrm{GC}}{\mathrm{DG}}=\dfrac{1}{3}
\end{align*}
(1)の解答
(1) 直線ABが点Gを通る場合について考える。
このとき,$\sankaku{AGD}$ の辺AG上に点Bがあるので,$\mathrm{BG}=\myBox{カ}$ である。
また,直線ABと直線DCが点Gで交わり,4点A,B,C,Dは同一円周上にあるので,$\mathrm{DC}=\myBox{キ}\sqrt{\myBox{ク}}$ である。

直線ABが点Gを通る図を描いて考えよう。
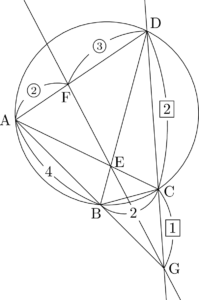

問題文から $\sankaku{AGD}$ に着目することが分かるから,チェバの定理を利用すればよいことが分かるね。
チェバの定理より
&\dfrac{\mathrm{GB}}{\mathrm{BA}}\Cdota\dfrac{\mathrm{AF}}{\mathrm{FD}}\Cdota\dfrac{\mathrm{DC}}{\mathrm{CG}}=1 \\[4pt]
&\dfrac{\mathrm{GB}}{4}\Cdota\dfrac{2}{3}\Cdota\dfrac{2}{1}=1 \\[4pt]
&\dfrac{1}{3}\mathrm{GB}=1 \\[4pt]
&\mathrm{GB}=3
\end{align*}

方べきの定理の利用を考えるときを覚えておこう。
- 弦の長さ
- 円の内部の点から円周上の点までの距離
- 円の外部の点から円周上の点までの距離

今回のBGは円の外部の点から円周上の点までの距離だから,方べきの定理を利用すれば良さそうだね。
方べきの定理より
&\mathrm{GC}\Cdota\mathrm{GD}=\mathrm{GB}\Cdota\mathrm{GA} \\[4pt]
&\dfrac{1}{2}\mathrm{DC}\Cdota\dfrac{3}{2}\mathrm{DC}=3\Cdota7 \\[4pt]
&\mathrm{DC}^2=2^2\Cdota7
\end{align*}
(2)の解答
(2) 四角形ABCDの外接円の直径が最小となる場合について考える。
このとき,四角形ABCDの外接円の直径は $\myBox{ケ}$ であり,$\kaku{BAC}=\myBox{コサ}\Deg$ である。
また,直線FEと直線ABの交点をHとするとき,$\dfrac{\mathrm{GC}}{\mathrm{DG}}=\dfrac{\mybox{エ}}{\mybox{オ}}$ の関係に着目してAHを求めると,$\mathrm{AH}=\myBox{シ}$ である。

次は「四角形ABCDの外接円の直径が最小となる場合」がどんなときかを考えよう。
まず,四角形ABCDの外接円は三角形ABCの外接円でもあることを考える。点Dの位置については,その外接円が決まれば,ただ1点に決まるから,三角形ABCの外接円の直径が最小になるときを考えれば良いことが分かる。三角形ABCの外接円の半径を $R$ とすると,正弦定理より
2R&=\dfrac{\mathrm{AB}}{\sin\kaku{ACB}}=\dfrac{4}{\sin\kaku{ACB}}
\end{align*}
ここまで考えれば,$\kaku{ACB}=90\Deg$ になることがあり得るなら,そのときが外接円の直径が最小になるときだと分かる。
いまABの長さは4,BCの長さは2で決まっているけど,$\kaku{ABC}$ は自由に動けるから,点Bを中心に点Cをぐるぐる回して考えよう。点Bを中心とする半径2の円周上のC$_1$の位置に,点Cがきたとき,$\kaku{ACB}=90\Deg$ になることが分かる。
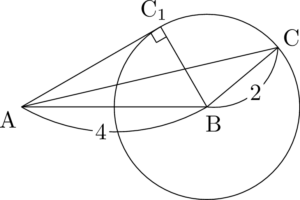
点CがC$_1$の位置にきたとき,三角形ABCの外接円の直径はABだから,四角形ABCDの外接円の直径は4である。$\myBox{ケ}=4$

このときの $\kaku{BAC}$ の大きさを求めよう。
三角形ABCは $1:2:\sqrt{3}$ の有名直角三角形だから,$\kaku{BAC}=30\Deg$

次の問題はまず,点Hの位置を確認しよう。
問題文にしたがって図を描くと次のようになる。
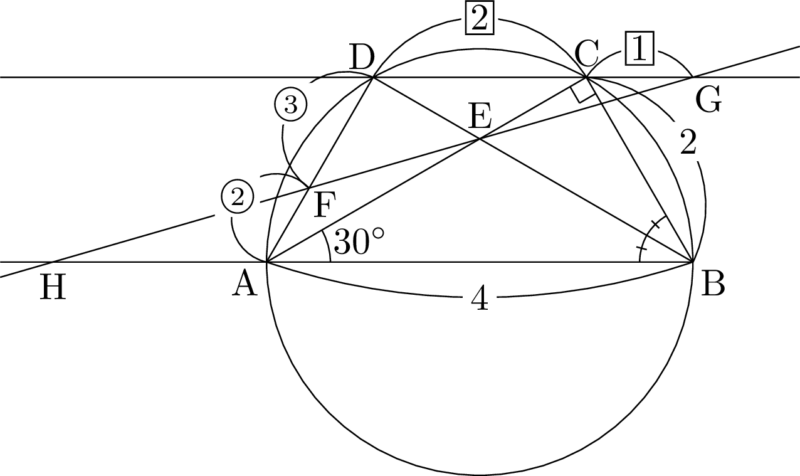
ここで $\kaku{ABC}=60\Deg$ であるから,$\kaku{ABD}=\kaku{CBD}=30\Deg$ となる。さらに円周角に着目して,$30\Deg$ になる角に同じ印を付けると次のようになる。
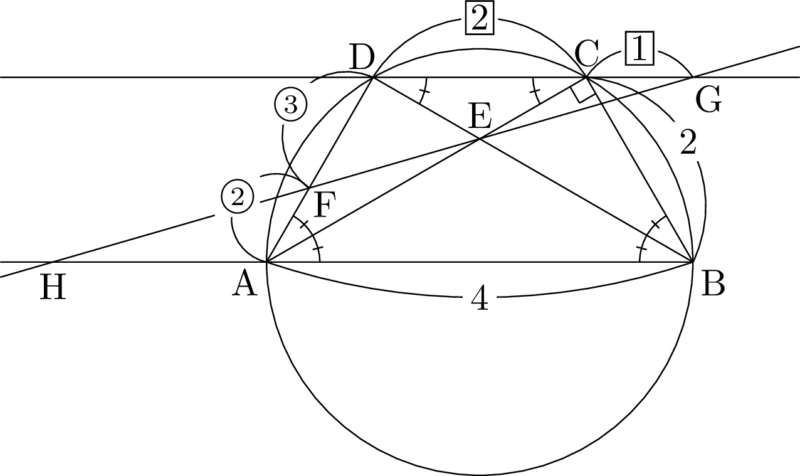
さらに $\mathrm{DC}=\mathrm{DB}=2$ であることが分かるから,$\mathrm{CG=1}$ であることも分かる。
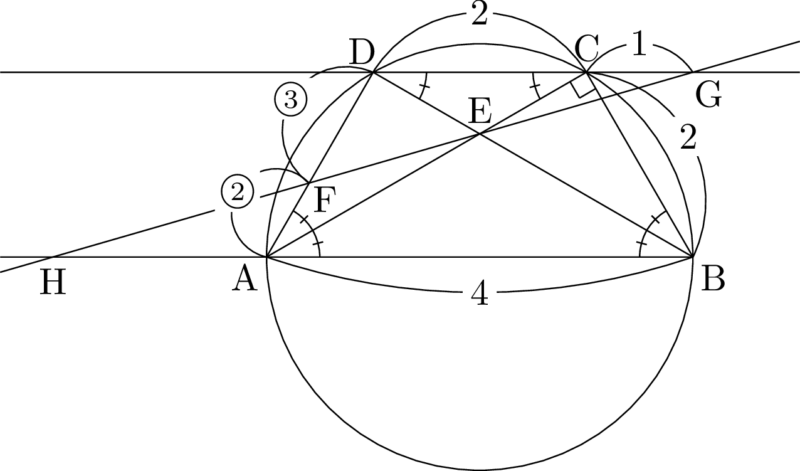

問題文に「$\dfrac{\mathrm{GC}}{\mathrm{DG}}=\dfrac{1}{3}$ の関係に着目してAHを求める」とあるから,GC,DGとAHの関係に着目しよう。
$\sankaku{EGD}$∽$\sankaku{EHB}$ であり,$\sankaku{ECD}$∽$\sankaku{EAB}$ である。よって $\dfrac{\mathrm{GC}}{\mathrm{DG}}=\dfrac{1}{3}$ より,$\dfrac{\mathrm{AH}}{\mathrm{BH}}=\dfrac{1}{3}$ が成り立つから
\mathrm{AH}&=\dfrac{1}{2}\mathrm{AB} \\[4pt]
&=\dfrac{1}{2}\Cdota4 \\[4pt]
&=2
\end{align*}

他の方法として,次のように求める方法もある。
$\sankaku{ECD}$∽$\sankaku{EAB}$ であり,相似比は $\mathrm{CD}:\mathrm{AB}=1:2$ であるから
\mathrm{CE}:\mathrm{EA}=1:2
\end{align*}
\mathrm{AH}:\mathrm{CG}&=\mathrm{AE}:\mathrm{EC} \\[4pt]
&=2:1
\end{align*}
\mathrm{AH}=2\mathrm{CG}=2
\end{align*}

時間内に解ければ良いので,どういう方法でも良いから解けるようにしよう。
2016年 センター数学ⅠA 平面図形を解いた感想

最初に参考図が用意されているものの,結局は自分で図を描かないといけないため,意外と時間がかかる。

また,問題文をよく読まずに解く人は,問題文に書かれているヒントに気付かないため,解くのに余計な時間がかかる可能性があるだろう。

問題文を読んでも分からない人は「このことより」や「○○の関係に着目して」と書かれている意味を理解できる実力を身に付ける必要があるだろう。




















