ここでは三角比を利用して様々な問題を解いてみましょう。
今回は正弦定理・余弦定理を使わずに解きます。
サイン・コサイン・タンジェントの意味を考えて解きましょう。
辺の長さを三角比を利用して表す

ヒロ
辺の長さを三角比を用いて表すことができるようになろう。
【辺の長さを三角比を用いて表す方法】
次のような直角三角形ABCを考える。

サイン・コサイン・タンジェントの値は
次のような直角三角形ABCを考える。

サイン・コサイン・タンジェントの値は
\begin{align*}
&\sin\theta=\dfrac{b}{c} \\[4pt]
&\cos\theta=\dfrac{a}{c} \\[4pt]
&\tan\theta=\dfrac{b}{a}
\end{align*}
であり,これらの式より&\sin\theta=\dfrac{b}{c} \\[4pt]
&\cos\theta=\dfrac{a}{c} \\[4pt]
&\tan\theta=\dfrac{b}{a}
\end{align*}
\begin{align*}
&a=c\cos\theta \\[4pt]
&b=c\sin\theta=a\tan\theta
\end{align*}
を導くことができる。&a=c\cos\theta \\[4pt]
&b=c\sin\theta=a\tan\theta
\end{align*}

ヒロ
元々の三角比の式から変形して $a,~b$ を $\theta$ を用いて表したが,直接書けるようにしよう。

ヒロ
個人的には,毎回「$\sin\theta=\dfrac{b}{c}$ の両辺に $c$ をかけることで,$b=c\sin\theta$」と変形するのでは「比」を正しく理解できていないように感じる。

ヒロ
次の問題の解き方によって,三角比を利用する考え方がスムーズに吸収できるかどうかが分かるかもしれない。
問題
問題次の直角三角形ABCを考える。丸囲み数字は辺の比を表すものとする。
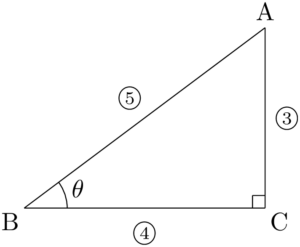
(1) $\text{AB}=15$ のとき,AC, BCの長さを求めよ。
(2) $\text{BC}=5$ のとき,AC, ABの長さを求めよ。

(1) $\text{AB}=15$ のとき,AC, BCの長さを求めよ。
(2) $\text{BC}=5$ のとき,AC, ABの長さを求めよ。
【(1)の考え方と解答】
真面目(?)に比が等しいことを考えて式を立てて,ACを求めると次のようになる。
この問題の場合は,$\text{AB}:\text{AC}=5:3$ から「ACの長さはABの $\dfrac{3}{5}$ である」とスムーズに読み替えることができるようにしよう。この考え方ができるようになると,
ここで $\dfrac{3}{5}$ は $\text{AC}:\text{AB}$ の比の値を表すが,これは $\sin\theta$ であるから,
BCの長さもABの長さの $\dfrac{4}{5}$ になることがすぐに分かる。この $\dfrac{4}{5}$ は角 $\theta$ を用いて $\cos\theta$ と表すことができるから,次のように,BCの長さを求めることができる。
真面目(?)に比が等しいことを考えて式を立てて,ACを求めると次のようになる。
\begin{align*}
\text{AB}:\text{AC}=5:3
\end{align*}
であるから\text{AB}:\text{AC}=5:3
\end{align*}
\begin{align*}
5\text{AC}&=3\text{AB} \\[4pt]
\text{AC}&=\dfrac{3}{5}\text{AB} \\[4pt]
&=\dfrac{3}{5}\times15=9
\end{align*}
この方法でもACの長さを求めることができるため,この方法でも良いのだが,小学校で学んだはずの「比」や「割合」を利用するべきである。5\text{AC}&=3\text{AB} \\[4pt]
\text{AC}&=\dfrac{3}{5}\text{AB} \\[4pt]
&=\dfrac{3}{5}\times15=9
\end{align*}
この問題の場合は,$\text{AB}:\text{AC}=5:3$ から「ACの長さはABの $\dfrac{3}{5}$ である」とスムーズに読み替えることができるようにしよう。この考え方ができるようになると,
\begin{align*}
\text{AC}&=\text{AB}\times\dfrac{3}{5} \\[4pt]
&=15\times\dfrac{3}{5}=12
\end{align*}
となり,比の式を立てることなくACの長さを直接求めることができるようになる。\text{AC}&=\text{AB}\times\dfrac{3}{5} \\[4pt]
&=15\times\dfrac{3}{5}=12
\end{align*}
ここで $\dfrac{3}{5}$ は $\text{AC}:\text{AB}$ の比の値を表すが,これは $\sin\theta$ であるから,
\begin{align*}
\text{AC}=\text{AB}\sin\theta
\end{align*}
となる。「比」や「割合」をしっかりと理解・活用している人は,三角比を学ぶ上でスタート時点で既に有利になっている。\text{AC}=\text{AB}\sin\theta
\end{align*}
BCの長さもABの長さの $\dfrac{4}{5}$ になることがすぐに分かる。この $\dfrac{4}{5}$ は角 $\theta$ を用いて $\cos\theta$ と表すことができるから,次のように,BCの長さを求めることができる。
\begin{align*}
\text{BC}&=\text{AB}\cos\theta \\[4pt]
&=15\times\dfrac{4}{5}=12
\end{align*}
\text{BC}&=\text{AB}\cos\theta \\[4pt]
&=15\times\dfrac{4}{5}=12
\end{align*}
(2) $\text{BC}=5$ のとき,AC, ABの長さを求めよ。
【(2)の考え方と解答】
BCの長さからACの長さを求めるから,$\dfrac{高さ}{底辺}$ を掛ければよい。

これは $\tan\theta$ であるから,
また,ABの長さを求める場合は,$\dfrac{斜辺}{底辺}$ を掛ければよい。あえて三角比を用いて表すと,次のようにABの長さを求めることができる。
BCの長さからACの長さを求めるから,$\dfrac{高さ}{底辺}$ を掛ければよい。

これは $\tan\theta$ であるから,
\begin{align*}
\text{AC}&=\text{BC}\tan\theta \\[4pt]
&=5\times\dfrac{3}{4}=\dfrac{15}{4}
\end{align*}
となる。\text{AC}&=\text{BC}\tan\theta \\[4pt]
&=5\times\dfrac{3}{4}=\dfrac{15}{4}
\end{align*}
また,ABの長さを求める場合は,$\dfrac{斜辺}{底辺}$ を掛ければよい。あえて三角比を用いて表すと,次のようにABの長さを求めることができる。
\begin{align*}
\text{AB}&=\text{BC}\times\dfrac{1}{\cos\theta} \\[4pt]
&=5\times\dfrac{5}{4}=\dfrac{25}{4}
\end{align*}
\text{AB}&=\text{BC}\times\dfrac{1}{\cos\theta} \\[4pt]
&=5\times\dfrac{5}{4}=\dfrac{25}{4}
\end{align*}

ヒロ
斜辺から高さを求めたり,斜辺から底辺を求める計算は頻出なので,比の式を経由せずに,三角比を用いて表せるようにしておこう。
辺の長さを求める問題
問題次の三角形において $a$ を求めよ。
(1)
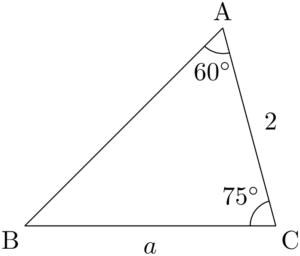
(2)
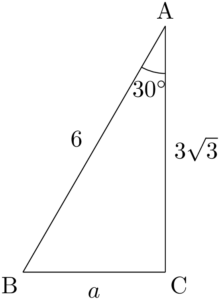
(1)

(2)

【(1)の考え方と解答】
60°が1つの角になるように,補助線を引いて直角三角形を作ろう。そのために点Cから辺ABに垂線CHを下ろすと,$\kaku{ACH}=30\Deg$, $\kaku{BCH}=45\Deg$ となる。
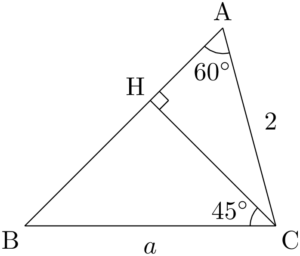
$\sankaku{ACH}$ に着目すると
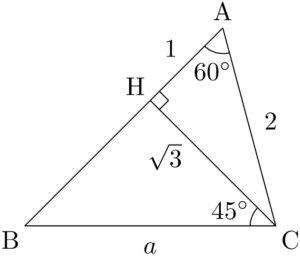
$\sankaku{BCH}$ に着目して
60°が1つの角になるように,補助線を引いて直角三角形を作ろう。そのために点Cから辺ABに垂線CHを下ろすと,$\kaku{ACH}=30\Deg$, $\kaku{BCH}=45\Deg$ となる。

$\sankaku{ACH}$ に着目すると
\begin{align*}
\text{AH}&=\text{AC}\cos60\Deg \\[4pt]
&=2\times\dfrac{1}{2}=1 \\[4pt]
\text{CH}&=\text{AC}\sin60\Deg \\[4pt]
&=2\times\dfrac{\sqrt{3}}{2}=\sqrt{3}
\end{align*}
\text{AH}&=\text{AC}\cos60\Deg \\[4pt]
&=2\times\dfrac{1}{2}=1 \\[4pt]
\text{CH}&=\text{AC}\sin60\Deg \\[4pt]
&=2\times\dfrac{\sqrt{3}}{2}=\sqrt{3}
\end{align*}

$\sankaku{BCH}$ に着目して
\begin{align*}
\text{BC}&=\text{CH}\times\dfrac{1}{\cos45\Deg} \\[4pt]
&=\sqrt{3}\times\sqrt{2}=\sqrt{6}
\end{align*}
よって,$a=\sqrt{6}$\text{BC}&=\text{CH}\times\dfrac{1}{\cos45\Deg} \\[4pt]
&=\sqrt{3}\times\sqrt{2}=\sqrt{6}
\end{align*}
【(2)の考え方と解答】
$\kaku{ACB}$ が90°かどうかは分からない。推測して $a$ を求める方法もあるが,今回は推測せずに考える。
点Cから辺ABに垂線CHを下ろす。
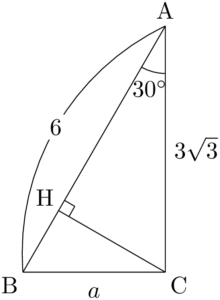
$\sankaku{ACH}$ に着目して
$\kaku{ACB}$ が90°かどうかは分からない。推測して $a$ を求める方法もあるが,今回は推測せずに考える。
点Cから辺ABに垂線CHを下ろす。

$\sankaku{ACH}$ に着目して
\begin{align*}
\text{CH}&=\text{AC}\sin30\Deg \\[4pt]
&=3\sqrt{3}\times\dfrac{1}{2}=\dfrac{3\sqrt{3}}{2} \\[4pt]
\text{AH}&=\text{AC}\cos30\Deg \\[4pt]
&=3\sqrt{3}\times\dfrac{\sqrt{3}}{2}=\dfrac{9}{2}
\end{align*}
これより\text{CH}&=\text{AC}\sin30\Deg \\[4pt]
&=3\sqrt{3}\times\dfrac{1}{2}=\dfrac{3\sqrt{3}}{2} \\[4pt]
\text{AH}&=\text{AC}\cos30\Deg \\[4pt]
&=3\sqrt{3}\times\dfrac{\sqrt{3}}{2}=\dfrac{9}{2}
\end{align*}
\begin{align*}
\text{BH}&=\text{AB}-\text{AH} \\[4pt]
&=6-\dfrac{9}{2}=\dfrac{3}{2}
\end{align*}
$\sankaku{BCH}$ に着目すると三平方の定理より\text{BH}&=\text{AB}-\text{AH} \\[4pt]
&=6-\dfrac{9}{2}=\dfrac{3}{2}
\end{align*}
\begin{align*}
\text{BC}&=\sqrt{\text{BH}^2+\text{CH}^2} \\[4pt]
&=\sqrt{\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3\sqrt{3}}{2}\right)^2} \\[4pt]
&=\sqrt{\dfrac{9}{4}+\dfrac{27}{4}}=\sqrt{9} \\[4pt]
&=3
\end{align*}
\text{BC}&=\sqrt{\text{BH}^2+\text{CH}^2} \\[4pt]
&=\sqrt{\left(\dfrac{3}{2}\right)^2+\left(\dfrac{3\sqrt{3}}{2}\right)^2} \\[4pt]
&=\sqrt{\dfrac{9}{4}+\dfrac{27}{4}}=\sqrt{9} \\[4pt]
&=3
\end{align*}

ヒロ
この結果から,三角形ABCは実は三角定規の直角三角形だったことが分かる。
辺の長さを求める問題2
問題図のような三角形ABCにおいて,$\text{AB}=4$, $\text{BC}=3$, $\kaku{ADC}=60\Deg$, $\kaku{ABC}=\theta$ であるとき,以下の問いに答えよ。
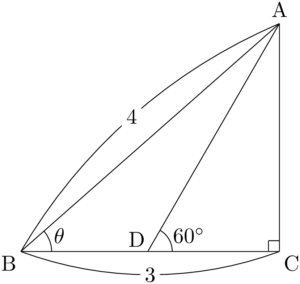
(1) $\sin\theta,~\tan\theta$ の値を求めよ。
(2) 線分AD,CDの長さを求めよ。

(1) $\sin\theta,~\tan\theta$ の値を求めよ。
(2) 線分AD,CDの長さを求めよ。
【(1)の考え方と解答】
$\sankaku{ABC}$ において三平方の定理を適用して
$\sankaku{ABC}$ において三平方の定理を適用して
\begin{align*}
\text{AC}=\sqrt{4^2-3^2}=\sqrt{7}
\end{align*}
となるから\text{AC}=\sqrt{4^2-3^2}=\sqrt{7}
\end{align*}
\begin{align*}
&\sin\theta=\dfrac{\sqrt{7}}{4} \\[4pt]
&\cos\theta=\dfrac{3}{4} \\[4pt]
&\tan\theta=\dfrac{\sqrt{7}}{3}
\end{align*}
&\sin\theta=\dfrac{\sqrt{7}}{4} \\[4pt]
&\cos\theta=\dfrac{3}{4} \\[4pt]
&\tan\theta=\dfrac{\sqrt{7}}{3}
\end{align*}
(2) 線分AD,CDの長さを求めよ。
【(2)の考え方と解答】
$\sankaku{ACD}$ に着目して考える。

$\text{AC}=\text{AD}\sin60\Deg$ であるから
$\sankaku{ACD}$ に着目して考える。

$\text{AC}=\text{AD}\sin60\Deg$ であるから
\begin{align*}
\text{AD}&=\dfrac{\text{AC}}{\sin60\Deg} \\[4pt]
&=\sqrt{7}\times\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{21}}{3}
\end{align*}
また,$\text{AC}=\text{CD}\tan60\Deg$ より\text{AD}&=\dfrac{\text{AC}}{\sin60\Deg} \\[4pt]
&=\sqrt{7}\times\dfrac{2}{\sqrt{3}}=\dfrac{2\sqrt{21}}{3}
\end{align*}
\begin{align*}
\text{CD}&=\dfrac{\text{AC}}{\tan60\Deg} \\[4pt]
&=\dfrac{\sqrt{7}}{\sqrt{3}}=\dfrac{\sqrt{21}}{3}
\end{align*}
\text{CD}&=\dfrac{\text{AC}}{\tan60\Deg} \\[4pt]
&=\dfrac{\sqrt{7}}{\sqrt{3}}=\dfrac{\sqrt{21}}{3}
\end{align*}
辺の長さを求める問題3
問題長方形ABCDにおいて,$\text{AB}=a$, $\kaku{ADB}=\theta$ とする。Aから対角線BDに下ろした垂線をAHとするとき,次の線分の長さを,$\theta$ の三角比と $a$ を用いて表せ。
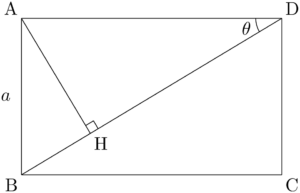
(1) AD
(2) BD
(3) AH

(1) AD
(2) BD
(3) AH
【(1)の考え方と解答】
いま求めたいのはADの長さだから,ADを含む三角形を考える。その中で,既に長さが分かっているABと $\theta$ を含む三角形を探すと $\sankaku{ABD}$ が見つかる。したがって
いま求めたいのはADの長さだから,ADを含む三角形を考える。その中で,既に長さが分かっているABと $\theta$ を含む三角形を探すと $\sankaku{ABD}$ が見つかる。したがって
\begin{align*}
&\text{AD}\tan\theta=\text{AB} \\[4pt]
&\text{AD}=\dfrac{\text{AB}}{\tan\theta} \\[4pt]
&\text{AD}=\dfrac{a}{\tan\theta}
\end{align*}
&\text{AD}\tan\theta=\text{AB} \\[4pt]
&\text{AD}=\dfrac{\text{AB}}{\tan\theta} \\[4pt]
&\text{AD}=\dfrac{a}{\tan\theta}
\end{align*}
【(2)の考え方と解答】
$\sankaku{ABD}$ に着目して
$\sankaku{ABD}$ に着目して
\begin{align*}
&\text{BD}\sin\theta=\text{AB} \\[4pt]
&\text{BD}=\dfrac{\text{AB}}{\sin\theta} \\[4pt]
&\text{BD}=\dfrac{a}{\sin\theta}
\end{align*}
&\text{BD}\sin\theta=\text{AB} \\[4pt]
&\text{BD}=\dfrac{\text{AB}}{\sin\theta} \\[4pt]
&\text{BD}=\dfrac{a}{\sin\theta}
\end{align*}
【(3)の考え方と解答】
$\sankaku{ABH}$ に着目すると,$\kaku{BAH}=\theta$ である。
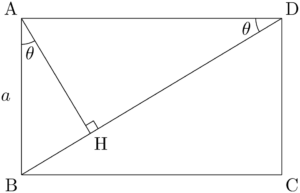
$\sankaku{ABH}$ に着目すると,$\kaku{BAH}=\theta$ である。

\begin{align*}
\text{AH}&=\text{AB}\cos\theta \\[4pt]
&=a\cos\theta
\end{align*}
\text{AH}&=\text{AB}\cos\theta \\[4pt]
&=a\cos\theta
\end{align*}

ヒロ
$\kaku{BAH}=\theta$ であることがすぐに分かるようにしよう。


















