Contents
2020年 東洋大
2020年 東洋大$-\dfrac{\pi}{4}\leqq\theta\leqq\dfrac{\pi}{4}$ のとき,関数 $f(\theta)=2\tan^2\theta-3\tan\theta+\dfrac{3}{2}$ の最小値は $\dfrac{\myhako}{\myhako}$,最大値は $\dfrac{\myhako}{\myhako}$ である。
【考え方と解答】
$\tan\theta=t$ とおくと,$-\dfrac{\pi}{4}\leqq\theta\leqq\dfrac{\pi}{4}$ のとき,$-1\leqq t\leqq1$ である。$y=f(\theta)$ とおくと,
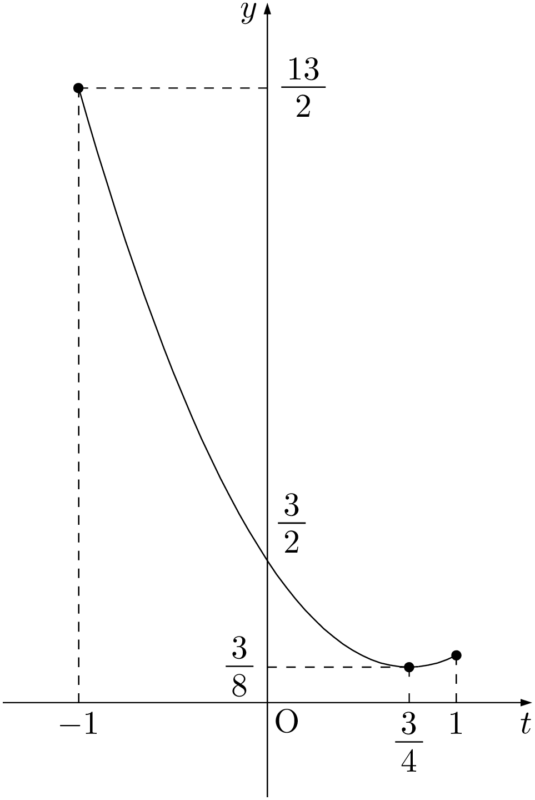
$t=\dfrac{3}{4}$ のとき,最小値 $\dfrac{3}{8}$ をとり,$t=-1$ のとき,最大値 $\dfrac{13}{2}$ をとる。
$\tan\theta=t$ とおくと,$-\dfrac{\pi}{4}\leqq\theta\leqq\dfrac{\pi}{4}$ のとき,$-1\leqq t\leqq1$ である。$y=f(\theta)$ とおくと,
\begin{align*}
y&=2t^2-3t+\dfrac{3}{2} \\[4pt]
&=2\left(t-\dfrac{3}{4}\right)^2+\dfrac{3}{8}
\end{align*}
y&=2t^2-3t+\dfrac{3}{2} \\[4pt]
&=2\left(t-\dfrac{3}{4}\right)^2+\dfrac{3}{8}
\end{align*}

$t=\dfrac{3}{4}$ のとき,最小値 $\dfrac{3}{8}$ をとり,$t=-1$ のとき,最大値 $\dfrac{13}{2}$ をとる。
2019年 明治薬科大
2019年 明治薬科大$a$ を正の定数,$n$ を自然数とする。$x$ の関数
(1) $n=1$ のとき,$y=f(x)$ は $0<x<a$ において $x=\myhako$ で最大値をとり,$y=g(x)$ は $-a<x<a$ において $x=\myhako$ で最大値をとる。
(2) $n=3$ のとき,$y=f(x)$ は $0<x<a$ において $x=\myhako$ で最大値をとる。
(3) $n=5$ のとき,$y=g(x)$ が $-a<x<a$ において最小値をとる $x$ の値の個数は $\myhako$ 個ある。
(4) $y=(g(x))^2$ が $-a<x<a$ において最大値または最小値をとる $x$ の値の個数は全部で $\myhako$ 個ある。
\begin{align*}
f(x)=\sin\dfrac{n\pi}{a}x,~g(x)=\cos\dfrac{n\pi}{2a}x
\end{align*}
を考える。f(x)=\sin\dfrac{n\pi}{a}x,~g(x)=\cos\dfrac{n\pi}{2a}x
\end{align*}
(1) $n=1$ のとき,$y=f(x)$ は $0<x<a$ において $x=\myhako$ で最大値をとり,$y=g(x)$ は $-a<x<a$ において $x=\myhako$ で最大値をとる。
(2) $n=3$ のとき,$y=f(x)$ は $0<x<a$ において $x=\myhako$ で最大値をとる。
(3) $n=5$ のとき,$y=g(x)$ が $-a<x<a$ において最小値をとる $x$ の値の個数は $\myhako$ 個ある。
(4) $y=(g(x))^2$ が $-a<x<a$ において最大値または最小値をとる $x$ の値の個数は全部で $\myhako$ 個ある。
【(1)の考え方と解答】
$n=1$ のとき,$f(x)=\sin\dfrac{\pi}{a}x$ である。$0<x<a$ のとき,$0<\dfrac{\pi}{a}x<\pi$ であるから,$\dfrac{\pi}{a}x=\dfrac{\pi}{2}$ すなわち $x=\dfrac{a}{2}$ のとき最大となる。
$n=1$ のとき,$g(x)=\cos\dfrac{\pi}{2a}x$ である。$-a<x<a$ のとき,$-\dfrac{\pi}{2}<\dfrac{\pi}{2a}x<\dfrac{\pi}{2}$ であるから,$\dfrac{\pi}{2a}x=0$ すなわち $x=0$ のとき最大となる。
$n=1$ のとき,$f(x)=\sin\dfrac{\pi}{a}x$ である。$0<x<a$ のとき,$0<\dfrac{\pi}{a}x<\pi$ であるから,$\dfrac{\pi}{a}x=\dfrac{\pi}{2}$ すなわち $x=\dfrac{a}{2}$ のとき最大となる。
$n=1$ のとき,$g(x)=\cos\dfrac{\pi}{2a}x$ である。$-a<x<a$ のとき,$-\dfrac{\pi}{2}<\dfrac{\pi}{2a}x<\dfrac{\pi}{2}$ であるから,$\dfrac{\pi}{2a}x=0$ すなわち $x=0$ のとき最大となる。
(2) $n=3$ のとき,$y=f(x)$ は $0<x<a$ において $x=\myhako$ で最大値をとる。
【(2)の考え方と解答】
$n=3$ のとき,$f(x)=\sin\dfrac{3\pi}{a}x$ である。$0<x<a$ のとき,$0<\dfrac{3\pi}{a}x<3\pi$ であるから,
$n=3$ のとき,$f(x)=\sin\dfrac{3\pi}{a}x$ である。$0<x<a$ のとき,$0<\dfrac{3\pi}{a}x<3\pi$ であるから,
\begin{align*} &\dfrac{3\pi}{a}x=\dfrac{\pi}{2},~\dfrac{5}{2}\pi \\[4pt] &x=\dfrac{a}{6},~\dfrac{5}{6}a \end{align*}
のとき最大になる。(3) $n=5$ のとき,$y=g(x)$ が $-a<x<a$ において最小値をとる $x$ の値の個数は $\myhako$ 個ある。
【(3)の考え方と解答】
$n=5$ のとき,$g(x)=\cos\dfrac{5\pi}{2a}x$ である。$-a<x<a$ のとき,$-\dfrac{5}{2}\pi<\dfrac{5\pi}{2a}x<\dfrac{5}{2}\pi$ であるから,
$n=5$ のとき,$g(x)=\cos\dfrac{5\pi}{2a}x$ である。$-a<x<a$ のとき,$-\dfrac{5}{2}\pi<\dfrac{5\pi}{2a}x<\dfrac{5}{2}\pi$ であるから,
\begin{align*} &\dfrac{5\pi}{2a}x=-\pi,~\pi \\[4pt] &x=-\dfrac{2}{5}\pi,~\dfrac{2}{5}\pi \end{align*}
のとき最小になる。よって,求める $x$ の値の個数は2個ある。(4) $y=(g(x))^2$ が $-a<x<a$ において最大値または最小値をとる $x$ の値の個数は全部で $\myhako$ 個ある。
【(4)の考え方と解答】
$-a<x<a$ のとき,$-\dfrac{n}{2}\pi<\dfrac{n\pi}{2a}x<\dfrac{n}{2}\pi$ であるから,$y=\cos^2\dfrac{n\pi}{2a}x$ が最大値または最小値をとるのは整数 $k$ を用いて
$-a<x<a$ のとき,$-\dfrac{n}{2}\pi<\dfrac{n\pi}{2a}x<\dfrac{n}{2}\pi$ であるから,$y=\cos^2\dfrac{n\pi}{2a}x$ が最大値または最小値をとるのは整数 $k$ を用いて
\begin{align*} &\dfrac{n\pi}{2a}x=\dfrac{\pi}{2}k \\[4pt] &x=\dfrac{ka}{n} \end{align*}
と表されるときである。$-a<x<a$ より \begin{align*} &-a<\dfrac{ka}{n}<a \\[4pt] &-n<k<n \end{align*}
これを満たす整数 $k$ は \begin{align*} k=0,~\pm1,~\pm2,~\cdots,~\pm(n-1) \end{align*}
であるから,$2n-1$ 個ある。よって,$x$ の個数も $2n-1$ 個である。

















