ここでは全体集合と補集合について説明します。
ある集合を考えるとき,その集合に属さないものを扱うときに,全体の集合が定まっていないと,本来は考えるはずのないものまで含まれてしまうことになります。
例えば「乃木坂46の1期生以外」と言った場合に「私のこと?」となる人は少ないです。
2期生や3期生のことを話しているのかなと考える人が多いと思います。
それは「乃木坂46」を全体として考えているからですね。
しかし日常会話ではそんな当たり前のことであっても,数学では予め決めておく必要があります。
例えば「偶数以外」と言われて奇数を考えるのは整数を全体として考えているからです。
このように話の対象となる全体(全体集合)とその部分集合のある集合以外の集合(補集合)について,その表し方や具体的な問題の解き方を学びましょう。
全体集合と補集合

ヒロ
全体集合と補集合の意味を理解しよう。
全体集合と補集合複数の集合について考えるとき,それらを含む大きな集合 $U$ を決めて,$U$ の部分集合だけを考えることが多い。このとき,集合 $U$ を全体集合という。
また,全体集合 $U$ の部分集合 $A$ に対して,$A$ に属さない $U$ の要素全体の
集合を $A$ の補集合といい $\overline{A}$ で表す。つまり

また,全体集合 $U$ の部分集合 $A$ に対して,$A$ に属さない $U$ の要素全体の
集合を $A$ の補集合といい $\overline{A}$ で表す。つまり
\begin{align*}
\overline{A}=\{x\mid x\in U~かつ~x\notin A\}
\end{align*}
ということである。\overline{A}=\{x\mid x\in U~かつ~x\notin A\}
\end{align*}

全体集合・空集合・補集合

ヒロ
全体集合・空集合・補集合について成り立つ式を知っておこう。
【全体集合・空集合・補集合】
$A$ の補集合 $\overline{A}$ の補集合は $A$ である。すなわち
$A$ の補集合 $\overline{A}$ の補集合は $A$ である。すなわち
\begin{align*}
\overline{\overline{A}}=A
\end{align*}
また,全体集合 $U$ と空集合 $\emptyset$ の関係は次のようになる。\overline{\overline{A}}=A
\end{align*}
\begin{align*}
\overline{U}=\emptyset,~\overline{\emptyset}=U
\end{align*}
これらのことから次のことも成り立つ。\overline{U}=\emptyset,~\overline{\emptyset}=U
\end{align*}
\begin{align*}
A\cap\overline{A}=\emptyset,~A\cup\overline{A}=U
\end{align*}
A\cap\overline{A}=\emptyset,~A\cup\overline{A}=U
\end{align*}

ヒロ
ベン図を見れば,これらのことが成り立つのはすぐに分かるだろう。
様々な集合

ヒロ
どの部分を表す集合かを判断できるようにしておこう。
問題次の集合が表す部分を次の図に斜線で表せ。
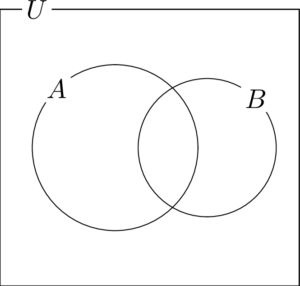
(1) $A\cap B$ (2) $A\cup B$
(3) $\overline{A}\cap B$ (4) $\overline{A}\cup B$
(5) $A\cap\overline{B}$ (6) $A\cup\overline{B}$
(7) $\overline{A}\cap\overline{B}$ (8) $\overline{A}\cup\overline{B}$
(9) $\overline{A\cap B}$ (10) $\overline{A\cup B}$

(1) $A\cap B$ (2) $A\cup B$
(3) $\overline{A}\cap B$ (4) $\overline{A}\cup B$
(5) $A\cap\overline{B}$ (6) $A\cup\overline{B}$
(7) $\overline{A}\cap\overline{B}$ (8) $\overline{A}\cup\overline{B}$
(9) $\overline{A\cap B}$ (10) $\overline{A\cup B}$

ヒロ
共通部分・和集合・補集合の記号を見間違えないようにして,1つずつ丁寧に考えるようにしよう。
【解答】
(1) $A\cap B$
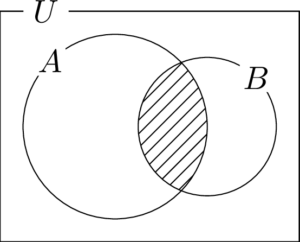
(2) $A\cup B$
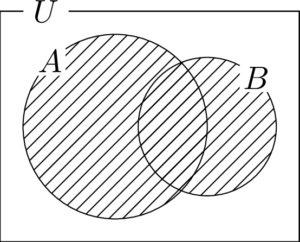
(3) $\overline{A}\cap B$

(4) $\overline{A}\cup B$

(5) $A\cap\overline{B}$

(6) $A\cup\overline{B}$

(7) $\overline{A}\cap\overline{B}$

(8) $\overline{A}\cup\overline{B}$

(9) $\overline{A\cap B}$

(10) $\overline{A\cup B}$

(1) $A\cap B$

(2) $A\cup B$

(3) $\overline{A}\cap B$

(4) $\overline{A}\cup B$

(5) $A\cap\overline{B}$

(6) $A\cup\overline{B}$

(7) $\overline{A}\cap\overline{B}$

(8) $\overline{A}\cup\overline{B}$

(9) $\overline{A\cap B}$

(10) $\overline{A\cup B}$


ヒロ
どの部分を表しているかがすぐに分かるようにしておこう。
全体集合と補集合に関する問題1

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題$U=\{x\mid 1\leqq x\leqq10,~x~は整数\}$ を全体集合とする。$U$ の部分集合 $A=\{1,~2,~3,~5,~7\}$,$B=\{2,~3,~8,~10\}$ について,次の集合を求めよ。
(1) $A\cap B$
(2) $\overline{B}$
(3) $\overline{A\cup B}$
(1) $A\cap B$
(2) $\overline{B}$
(3) $\overline{A\cup B}$
【考え方と解答】
(1) $A$ と $B$ の共通部分であるから
(1) $A$ と $B$ の共通部分であるから
\begin{align*}
A\cap B=\{2,~3\}
\end{align*}
(2) $U$ のうち $B$ 以外の集合であるからA\cap B=\{2,~3\}
\end{align*}
\begin{align*}
\overline{B}=\{1,~4,~5,~6,~7,~9\}
\end{align*}
(3) $A\cup B$ は $A$ と $B$ の和集合であるから\overline{B}=\{1,~4,~5,~6,~7,~9\}
\end{align*}
\begin{align*}
A\cup B=\{1,~2,~3,~5,~7,~8,~10\}
\end{align*}
$\overline{A\cup B}$ は $A\cup B$ の補集合であるからA\cup B=\{1,~2,~3,~5,~7,~8,~10\}
\end{align*}
\begin{align*}
\overline{A\cup B}=\{4,~6,~9\}
\end{align*}
\overline{A\cup B}=\{4,~6,~9\}
\end{align*}
全体集合と補集合に関する問題2

ヒロ
次も実際に定期テストで出題された問題。
問題全体集合
\begin{align*}
U=\{1,~2,~3,~4,~5,~6,~7,~8,~9,~10\}
\end{align*}
の部分集合 $A,~B$ について,U=\{1,~2,~3,~4,~5,~6,~7,~8,~9,~10\}
\end{align*}
\begin{align*}
&A\cap B=\{3,~6,~8\} \\[4pt]
&\overline{A}\cap\overline{B}=\{4,~5,~7\} \\[4pt]
&A\cap\overline{B}=\{1,~10\}
\end{align*}
とする。集合 $B$ を求めよ。&A\cap B=\{3,~6,~8\} \\[4pt]
&\overline{A}\cap\overline{B}=\{4,~5,~7\} \\[4pt]
&A\cap\overline{B}=\{1,~10\}
\end{align*}

ヒロ
図を利用して解いていこう。
【考え方と解答】
$A$ と $B$ の共通部分が空集合ではないから,まず次のような図を描こう。

$A\cap B=\{3,~6,~8\}$ であるから,$A$ と $B$ の両方に属する部分に3,6,8の3つの数字を書こう。
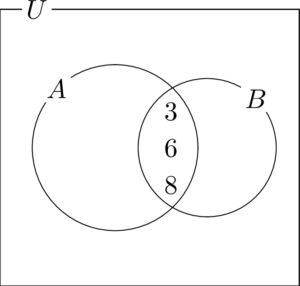
次の $\overline{A}\cap\overline{B}=\{4,~5,~7\}$ から,$A$ と $B$ の両方の外の部分に4,5,7があることが分かる。
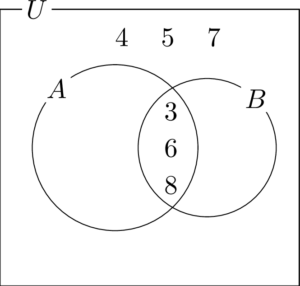
$A\cap\overline{B}=\{1,~10\}$ から $A$ の中で $B$ の外にある部分に1と10があることが分かる。
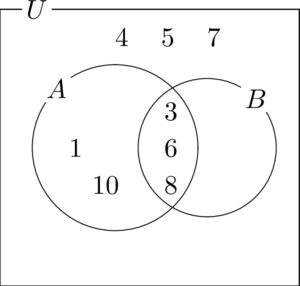
残った2と9をまだ空白になっている $A$ の外側で $B$ の内部に書いて完成。
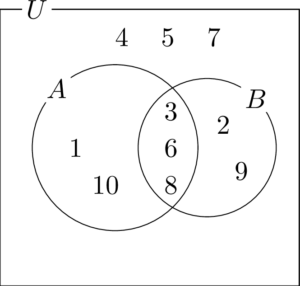
求めるものは集合 $B$ であるから,
$A$ と $B$ の共通部分が空集合ではないから,まず次のような図を描こう。

$A\cap B=\{3,~6,~8\}$ であるから,$A$ と $B$ の両方に属する部分に3,6,8の3つの数字を書こう。

次の $\overline{A}\cap\overline{B}=\{4,~5,~7\}$ から,$A$ と $B$ の両方の外の部分に4,5,7があることが分かる。

$A\cap\overline{B}=\{1,~10\}$ から $A$ の中で $B$ の外にある部分に1と10があることが分かる。

残った2と9をまだ空白になっている $A$ の外側で $B$ の内部に書いて完成。

求めるものは集合 $B$ であるから,
\begin{align*}
B=\{2,~3,~6,~8,~9\}
\end{align*}
B=\{2,~3,~6,~8,~9\}
\end{align*}


















