Contents
3つの線分の長さの和に関する問題
2007年 慶應義塾大座標平面上に点A$(4,~3)$ と点B$(8,~2)$,直線 $l:y=x$ と直線 $m:y=0$ が与えられている。
(1) 直線 $l$ に関して点Aと対称な点をA$’$ とし,直線 $m$ に関して点Bと対称な点をB$’$ とする。A$’$ とB$’$ の座標はそれぞれA$’\left(\myhako,~\myhako\right)$,B$’\left(\myhako,~\myhako\right)$ である。
(2) 点Pが直線 $l$ 上を動くとき,線分の長さの和 $\text{AP}+\text{PB}$ が最小となるPの座標はP$\left(\dfrac{\myhako}{\myhako},~\dfrac{\myhako}{\myhako}\right)$ である。
(3) 点Qが直線 $l$ 上を動き,点Rが直線 $m$ 上を動くとき,線分の長さの和 $\text{AQ}+\text{QR}+\text{RB}$ が最小となるQ,Rの座標はそれぞれQ$\left(\dfrac{\myhako}{\myhako},~\dfrac{\myhako}{\myhako}\right)$,R$\left(\dfrac{\myhako}{\myhako},~0\right)$ である。
(1) 直線 $l$ に関して点Aと対称な点をA$’$ とし,直線 $m$ に関して点Bと対称な点をB$’$ とする。A$’$ とB$’$ の座標はそれぞれA$’\left(\myhako,~\myhako\right)$,B$’\left(\myhako,~\myhako\right)$ である。
(2) 点Pが直線 $l$ 上を動くとき,線分の長さの和 $\text{AP}+\text{PB}$ が最小となるPの座標はP$\left(\dfrac{\myhako}{\myhako},~\dfrac{\myhako}{\myhako}\right)$ である。
(3) 点Qが直線 $l$ 上を動き,点Rが直線 $m$ 上を動くとき,線分の長さの和 $\text{AQ}+\text{QR}+\text{RB}$ が最小となるQ,Rの座標はそれぞれQ$\left(\dfrac{\myhako}{\myhako},~\dfrac{\myhako}{\myhako}\right)$,R$\left(\dfrac{\myhako}{\myhako},~0\right)$ である。
【(1)の考え方と解答】
「直線に関して対称な点」の最後に書いたように,直線 $y=x$ に関して対称な点の座標は,$x$ 座標と $y$ 座標を入れ換えれば良いから,A$'(3,~4)$ である。また,直線 $m:y=0$ は $x$ 軸であるから,$y$ 座標の符号を変えて,B$'(8,~-2)$ となる。
「直線に関して対称な点」の最後に書いたように,直線 $y=x$ に関して対称な点の座標は,$x$ 座標と $y$ 座標を入れ換えれば良いから,A$'(3,~4)$ である。また,直線 $m:y=0$ は $x$ 軸であるから,$y$ 座標の符号を変えて,B$'(8,~-2)$ となる。
(2) 点Pが直線 $l$ 上を動くとき,線分の長さの和 $\text{AP}+\text{PB}$ が最小となるPの座標はP$\left(\dfrac{\myhako}{\myhako},~\dfrac{\myhako}{\myhako}\right)$ である。
【(2)の考え方と解答】
直線 $l$ の方程式が $y=x$ であることから,平面上の点の $x$ 座標と $y$ 座標が等しいとき,その点は $l$ 上にある。つまり,点の $x$ 座標と $y$ 座標の大小関係を確認することで,$l$ に関して同じ側にあるか反対側にあるかを判別できる。
2点A,Bの座標をみると,ともに $x$ 座標が $y$ 座標より大きいから直線 $l$ に対して同じ側にあることが分かる。図を描いて確認しても良い。
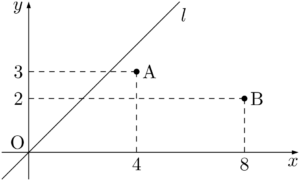
2点A,Bが $l$ に対して反対側になるように,一方の点を $l$ に関して対称移動させよう。(1)で $l$ に関して点Aと対称な点A$’$ を求めているから,この点を利用しよう。
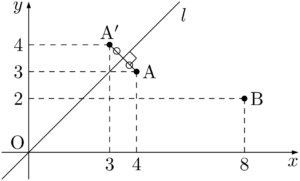
点Pが直線A$’$Bと直線 $l$ の交点に一致するとき,$\text{AP}+\text{PB}$ が最小になる。直線A$’$Bの傾きは
直線 $l$ の方程式が $y=x$ であることから,平面上の点の $x$ 座標と $y$ 座標が等しいとき,その点は $l$ 上にある。つまり,点の $x$ 座標と $y$ 座標の大小関係を確認することで,$l$ に関して同じ側にあるか反対側にあるかを判別できる。
2点A,Bの座標をみると,ともに $x$ 座標が $y$ 座標より大きいから直線 $l$ に対して同じ側にあることが分かる。図を描いて確認しても良い。

2点A,Bが $l$ に対して反対側になるように,一方の点を $l$ に関して対称移動させよう。(1)で $l$ に関して点Aと対称な点A$’$ を求めているから,この点を利用しよう。

点Pが直線A$’$Bと直線 $l$ の交点に一致するとき,$\text{AP}+\text{PB}$ が最小になる。直線A$’$Bの傾きは
\begin{align*}
\dfrac{2-4}{8-3}=-\dfrac{2}{5}
\end{align*}
であるから,直線の方程式は\dfrac{2-4}{8-3}=-\dfrac{2}{5}
\end{align*}
\begin{align*}
&y=-\dfrac{2}{5}(x-3)+4 \\[4pt]
&y=-\dfrac{2}{5}x+\dfrac{26}{5}
\end{align*}
$y=x$ と連立させて,$y$ を消去すると&y=-\dfrac{2}{5}(x-3)+4 \\[4pt]
&y=-\dfrac{2}{5}x+\dfrac{26}{5}
\end{align*}
\begin{align*}
&x=-\dfrac{2}{5}x+\dfrac{26}{5} \\[4pt]
&5x=-2x+26 \\[4pt]
&x=\dfrac{26}{7}
\end{align*}
よって,求める点Pの座標は $\left(\dfrac{26}{7},~\dfrac{26}{7}\right)$&x=-\dfrac{2}{5}x+\dfrac{26}{5} \\[4pt]
&5x=-2x+26 \\[4pt]
&x=\dfrac{26}{7}
\end{align*}

ヒロ
係数が分数の方程式を解くときは,通分するのではなく,両辺に同じ数をかけて分母を払った方が良い。
(3) 点Qが直線 $l$ 上を動き,点Rが直線 $m$ 上を動くとき,線分の長さの和 $\text{AQ}+\text{QR}+\text{RB}$ が最小となるQ,Rの座標はそれぞれQ$\left(\dfrac{\myhako}{\myhako},~\dfrac{\myhako}{\myhako}\right)$,R$\left(\dfrac{\myhako}{\myhako},~0\right)$ である。
【(3)の考え方と解答】
(2)で直線 $l$ に着目したときに,2点A,Bが $l$ に対して同じ側にあったから,反対側になるように点A$’$ をとって考えた。これによって,点Qが $l$ 上にあるときは常に $\text{AQ}+\text{QB}=\text{A}’\text{Q}+\text{QB}$ が成り立つ。したがって,直線 $l$ を気にする必要がなくなったので,直線 $m$ に着目しよう。
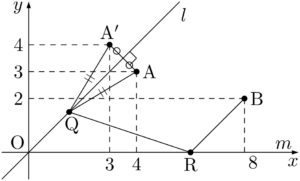
2点A$’$,Bは直線 $m$ に対して同じ側にあるから,2点A$’$,Bのうちどちらかを $m$ に関して対称移動させる。もし点A$’$ を対称移動させて点A$’$$’$ を考えると,$l$ に対して2点A$’$$’$,Bが同じ側にあるから,これでは意味がない。つまり点Bを $m$ に関して対称移動させればよいことが分かる。また,このことは(1)でB$’$ を求めたことを考えると「誘導になっているんだ」と納得がいくだろう。
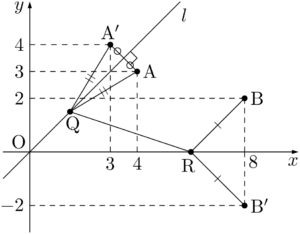
$\text{RB}=\text{RB}’$ であるから,
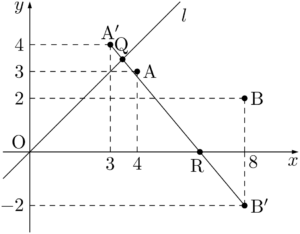
直線A$’$B$’$ の傾きは
(2)で直線 $l$ に着目したときに,2点A,Bが $l$ に対して同じ側にあったから,反対側になるように点A$’$ をとって考えた。これによって,点Qが $l$ 上にあるときは常に $\text{AQ}+\text{QB}=\text{A}’\text{Q}+\text{QB}$ が成り立つ。したがって,直線 $l$ を気にする必要がなくなったので,直線 $m$ に着目しよう。

2点A$’$,Bは直線 $m$ に対して同じ側にあるから,2点A$’$,Bのうちどちらかを $m$ に関して対称移動させる。もし点A$’$ を対称移動させて点A$’$$’$ を考えると,$l$ に対して2点A$’$$’$,Bが同じ側にあるから,これでは意味がない。つまり点Bを $m$ に関して対称移動させればよいことが分かる。また,このことは(1)でB$’$ を求めたことを考えると「誘導になっているんだ」と納得がいくだろう。

$\text{RB}=\text{RB}’$ であるから,
\begin{align*}
&\text{AQ}+\text{QR}+\text{RB}=\text{A}’\text{Q}+\text{QR}+\text{RB}’
\end{align*}
となる。これが最小になるのは,線分A$’$B$’$ 上に2点Q,Rがあるときで,最小値は線分A$’$B$’$ の長さとなる。&\text{AQ}+\text{QR}+\text{RB}=\text{A}’\text{Q}+\text{QR}+\text{RB}’
\end{align*}

直線A$’$B$’$ の傾きは
\begin{align*}
\dfrac{4-(-2)}{3-8}=-\dfrac{6}{5}
\end{align*}
であるから,直線A$’$B$’$ の方程式は\dfrac{4-(-2)}{3-8}=-\dfrac{6}{5}
\end{align*}
\begin{align*}
&y=-\dfrac{6}{5}(x-3)+4 \\[4pt]
&y=-\dfrac{6}{5}x+\dfrac{38}{5}~\cdots\cdots①
\end{align*}
①と $y=x$ を連立させて,$y$ を消去すると&y=-\dfrac{6}{5}(x-3)+4 \\[4pt]
&y=-\dfrac{6}{5}x+\dfrac{38}{5}~\cdots\cdots①
\end{align*}
\begin{align*}
&x=-\dfrac{6}{5}x+\dfrac{38}{5} \\[4pt]
&5x=-6x+38 \\[4pt]
&x=\dfrac{38}{11}
\end{align*}
また,①と $y=0$ を連立させると&x=-\dfrac{6}{5}x+\dfrac{38}{5} \\[4pt]
&5x=-6x+38 \\[4pt]
&x=\dfrac{38}{11}
\end{align*}
\begin{align*}
&-\dfrac{6}{5}x+\dfrac{38}{5}=0 \\[4pt]
&x=\dfrac{19}{3}
\end{align*}
よって,求める点Q,Rの座標はそれぞれ&-\dfrac{6}{5}x+\dfrac{38}{5}=0 \\[4pt]
&x=\dfrac{19}{3}
\end{align*}
\begin{align*}
\text{Q}\left(\dfrac{38}{11},~\dfrac{38}{11}\right),\text{R}\left(\dfrac{19}{3},~0\right)
\end{align*}
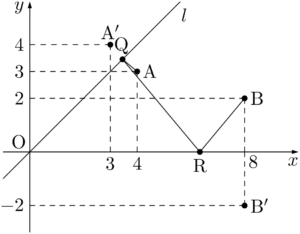
※点Aから点Bへの最短経路を示すと次のようになる。\text{Q}\left(\dfrac{38}{11},~\dfrac{38}{11}\right),\text{R}\left(\dfrac{19}{3},~0\right)
\end{align*}



















