Contents
円とy軸と平行でない直線の共有点

ヒロ
円 $C:x^2+y^2+lx+my+n=0$ と直線 $l:y=ax+b$ の共有点を求める方法を説明する。
先程と同様に,連立方程式
\begin{align*}
\begin{cases}
x^2+y^2+lx+my+n=0 &~\cdots\cdots① \\[4pt]
y=ax+b &~\cdots\cdots②
\end{cases}
\end{align*}
を解く。②を①に代入すると\begin{cases}
x^2+y^2+lx+my+n=0 &~\cdots\cdots① \\[4pt]
y=ax+b &~\cdots\cdots②
\end{cases}
\end{align*}
\begin{align*}
&x^2+(ax+b)^2+lx+m(ax+b)+n=0 \\[4pt]
&(a^2+1)x^2+(2ab+l+ma)x+b^2+mb+n=0~\cdots\cdots③
\end{align*}
③を解くことで,共有点の $x$ 座標が得られる。得られた $x$ 座標を②に代入して計算することで,共有点の $y$ 座標も得られる。&x^2+(ax+b)^2+lx+m(ax+b)+n=0 \\[4pt]
&(a^2+1)x^2+(2ab+l+ma)x+b^2+mb+n=0~\cdots\cdots③
\end{align*}
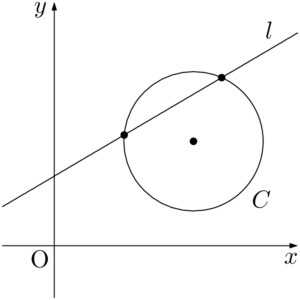
円と直線の共有点を求める問題【立教大】
2009年 立教大$x^2+y^2=5$ と $y=x+1$ の交点は $(1,~2)$ と $\left(\myhako,~\myhako\right)$ である。
【考え方と解答】
連立方程式を解いて交点の座標を求めよう。$y=x+1$ を $x^2+y^2=5$ に代入して
連立方程式を解いて交点の座標を求めよう。$y=x+1$ を $x^2+y^2=5$ に代入して
\begin{align*}
&x^2+(x+1)^2=5 \\[4pt]
&2x^2+2x-4=0 \\[4pt]
&x^2+x-2=0 \\[4pt]
&(x-1)(x+2)=0 \\[4pt]
&x=1,~-2
\end{align*}
$x=1$ のとき,$y=2$ となり,これは与えられている交点の座標である。$x=-2$ のとき,$y=-1$ となるから,求める交点の座標は $(-2,~-1)$ である。&x^2+(x+1)^2=5 \\[4pt]
&2x^2+2x-4=0 \\[4pt]
&x^2+x-2=0 \\[4pt]
&(x-1)(x+2)=0 \\[4pt]
&x=1,~-2
\end{align*}

ヒロ
今回の問題では,円と直線と書かれていないが,円と直線の2つの交点のうち,一方が与えられていて,もう一方の交点の座標を求める問題だと分かる。

ヒロ
円と直線の図形的性質を利用すると,別の解法を考えることができる。
【円と直線の2つの共有点】
円 $C$ と直線 $l$ が2点P,Qで交わっている次の図の状態を考える。
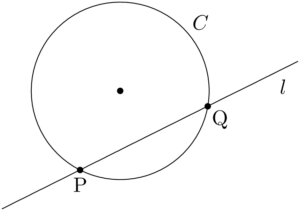
円の中心を通り,$l$ に垂直な直線を $n$ とすると,2点P,Qは互いに $n$ に関して対称な点であるといえる。
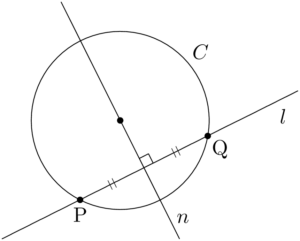
つまり,2つの共有点のうち,一方が分かっていれば「直線に関して対称な点」を求める要領でもう一方の点の座標を求めることができる。
$x^2+y^2=5$ と $y=x+1$ の交点は $(1,~2)$ と $\left(\myhako,~\myhako\right)$ である。
【別の考え方と解答】
$C:x^2+y^2=5$,$l:y=x+1$ とする。円 $C$ の中心は原点であり,$l$ の傾きは1であるから,原点を通り,$l$ に垂直な直線の方程式は $y=-x$ である。つまり,求めるものは,直線 $y=-x$ に関して点$(1,~2)$ と対称な点の座標である。さらに,直線 $y=-x$ に関する対称移動を覚えている人にとっては,「$x$ 座標と $y$ 座標を入れ換えて符号を逆にすれば良いだけ」だから,求める交点の座標は $(-2,~-1)$ であることがすぐに分かる。
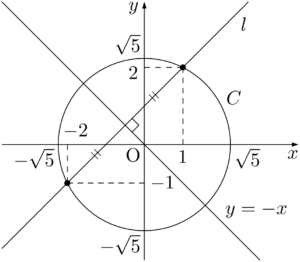
$C:x^2+y^2=5$,$l:y=x+1$ とする。円 $C$ の中心は原点であり,$l$ の傾きは1であるから,原点を通り,$l$ に垂直な直線の方程式は $y=-x$ である。つまり,求めるものは,直線 $y=-x$ に関して点$(1,~2)$ と対称な点の座標である。さらに,直線 $y=-x$ に関する対称移動を覚えている人にとっては,「$x$ 座標と $y$ 座標を入れ換えて符号を逆にすれば良いだけ」だから,求める交点の座標は $(-2,~-1)$ であることがすぐに分かる。



















