2曲線が接する条件について説明します。
入試問題の中には,問題文に「2曲線が接する」とはどういうことかが書かれているものもありますが,理解しておいた方が良いでしょう。
様々な問題を解けるようにしましょう。
2曲線が接するとは

ヒロ
まずは2曲線が接するとはどういうことかを理解しよう。
2曲線が接する「2曲線が接する」とは「2曲線が1点を共有し,かつ共有点における接線が一致すること」である。
具体的には,2つの曲線 $y=f(x),~y=g(x)$ が $x$ 座標が $t$ の点で接しているとき,
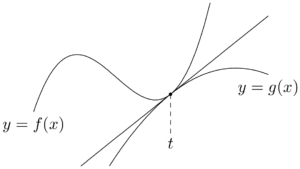
具体的には,2つの曲線 $y=f(x),~y=g(x)$ が $x$ 座標が $t$ の点で接しているとき,
\begin{align*}
f(t)=g(t)~~かつ~~f'(t)=g'(t)
\end{align*}
が成り立つ。接点における接線を2つの曲線の共通接線という。f(t)=g(t)~~かつ~~f'(t)=g'(t)
\end{align*}

2019年 東京理科大
2019年 東京理科大座標平面において曲線 $C_1:y=x^3-x$ と曲線 $C_2:y=x^2+a$ を考える。ただし,$a$ は実数の定数である。2つの曲線 $C_1,~C_2$ が接するのは $a=-\myhako$ と $a=\dfrac{\myhako}{\myhako}$ のときである。ただし,「2つの曲線が接する」とは,「2つの曲線が共有点をもち,その点において共通の接線をもつ」ことを意味する。

ヒロ
「2つの曲線が接する」とはどういうことかの説明が書かれているため,解きやすくなっている。
【解答と考え方】
$f(x)=x^3-x$, $g(x)=x^2+a$ とすると
$f(x)=x^3-x$, $g(x)=x^2+a$ とすると
\begin{align*}
f'(x)=3x^2-1,~g'(x)=2x
\end{align*}
2曲線 $C_1,~C_2$ が $x$ 座標が $t$ の点で接しているとすると,f'(x)=3x^2-1,~g'(x)=2x
\end{align*}
\begin{align*}
f(t)=g(t)~\cdots\cdots①,~f'(t)=g'(t)~\cdots\cdots②
\end{align*}
が成り立つ。②よりf(t)=g(t)~\cdots\cdots①,~f'(t)=g'(t)~\cdots\cdots②
\end{align*}
\begin{align*}
&3t^2-1=2t \\[4pt]
&3t^2-2t-1=0 \\[4pt]
&(t-1)(3t+1)=0 \\[4pt]
&t=1,~-\dfrac{1}{3}
\end{align*}
①より&3t^2-1=2t \\[4pt]
&3t^2-2t-1=0 \\[4pt]
&(t-1)(3t+1)=0 \\[4pt]
&t=1,~-\dfrac{1}{3}
\end{align*}
\begin{align*}
&t^3-t=t^2+a \\[4pt]
&a=t^3-t^2-t
\end{align*}
$t=1$ のとき,&t^3-t=t^2+a \\[4pt]
&a=t^3-t^2-t
\end{align*}
\begin{align*}
a=1-1-1=-1
\end{align*}
$t=-\dfrac{1}{3}$ のとき,a=1-1-1=-1
\end{align*}
\begin{align*}
a&=-\dfrac{1}{27}-\dfrac{1}{9}+\dfrac{1}{3} \\[4pt]
&=\dfrac{5}{27}
\end{align*}
よって,$a=-1,~\dfrac{5}{27}$a&=-\dfrac{1}{27}-\dfrac{1}{9}+\dfrac{1}{3} \\[4pt]
&=\dfrac{5}{27}
\end{align*}
2018年 自治医科大
2018年 自治医科大2つの曲線 $C_1:y=x^3-x^2-12x-1$,$C_2:y=-x^3+2x^2+a$($a$ は自然数)について考える。曲線 $C_1$ と $C_2$ が接するとき,$a$ の値を求めよ。
【解答と考え方】
\begin{align*}
&f(x)=x^3-x^2-12x-1 \\[4pt]
&g(x)=-x^3+2x^2+a
\end{align*}
とすると,&f(x)=x^3-x^2-12x-1 \\[4pt]
&g(x)=-x^3+2x^2+a
\end{align*}
\begin{align*}
&f'(t)=3x^2-2x-12 \\[4pt]
&g'(t)=-3x^2+4x
\end{align*}
曲線 $C_1$ と $C_2$ が $x$ 座標が $t$ の点で接するとき&f'(t)=3x^2-2x-12 \\[4pt]
&g'(t)=-3x^2+4x
\end{align*}
\begin{align*}
f(t)=g(t)~\cdots\cdots①,~f'(t)=g'(t)~\cdots\cdots②
\end{align*}
が成り立つ。②よりf(t)=g(t)~\cdots\cdots①,~f'(t)=g'(t)~\cdots\cdots②
\end{align*}
\begin{align*}
&3t^2-2t-12=-3t^2+4t \\[4pt]
&6t^2-6t-12=0 \\[4pt]
&t^2-t-2=0 \\[4pt]
&(t-2)(t+1)=0 \\[4pt]
&t=2,~-1
\end{align*}
①より&3t^2-2t-12=-3t^2+4t \\[4pt]
&6t^2-6t-12=0 \\[4pt]
&t^2-t-2=0 \\[4pt]
&(t-2)(t+1)=0 \\[4pt]
&t=2,~-1
\end{align*}
\begin{align*}
&t^3-t^2-12t-1=-t^3+2t^2+a \\[4pt]
&a=2t^3-3t^2-12t-1
\end{align*}
$t=2$ のとき&t^3-t^2-12t-1=-t^3+2t^2+a \\[4pt]
&a=2t^3-3t^2-12t-1
\end{align*}
\begin{align*}
a=16-12-24-1=-21
\end{align*}
$t=-1$ のときa=16-12-24-1=-21
\end{align*}
\begin{align*}
a=-2-3+12-1=6
\end{align*}
$a$ は自然数であるから,$a=6$a=-2-3+12-1=6
\end{align*}

ヒロ
問題文に書かれている条件「$a$ は自然数」に注意しよう。


















