不等式の証明問題における考え方と解法について説明します。
この記事で扱う問題は,微分を利用して証明する問題ですが,そもそも,不等式を証明する問題を見たときに,「これは微分を利用する問題だな」と判断するポイントを知っておく必要があります。
一般に,不等式の証明では,グラフを利用して証明する方法があります。2次関数のグラフであれば,平方完成することでグラフを描くことができるため,微分は必要ありません。しかし,3次関数や4次関数の場合は,微分することで関数の増減が分かるから,グラフを描くことができます。
したがって,不等式に現れる文字が1種類で,3次式の場合は,3次関数のグラフを利用する方法が解法の1つとして考えられます。その場合は,微分を利用することで与えられた不等式を証明できるかもしれません。
Contents
2011年 神戸大
2011年 神戸大$x\geqq4$ をみたすすべての実数 $x$ に対して,$x^3>3x^2+3x+1$ が成り立つことを示せ。

ヒロ
不等式の証明問題の考え方として,次のことを知っておこう。
不等式の証明方法$x$ に関する不等式 $f(x)\geqq g(x)$ を証明するためには,「$f(x)-g(x)\geqq0$」を証明しよう。$h(x)=f(x)-g(x)$ とおくと $h(x)\geqq0$ であることを示すことになるが,これは「$h(x)$ の最小値が0以上」と読み替えるようにしよう。
【解答と考え方】
$f(x)=x^3-3x^2-3x-1$ とおくと
よって,$f(x)$ の増減は次のようになる。
$f(x)=x^3-3x^2-3x-1$ とおくと
\begin{align*}
f'(x)&=3x^2-6x-3 \\[4pt]
&=3(x^2-2x-1)
\end{align*}
$f'(x)=0$ とすると,$x=1\pm\sqrt{2}$f'(x)&=3x^2-6x-3 \\[4pt]
&=3(x^2-2x-1)
\end{align*}
よって,$f(x)$ の増減は次のようになる。
\begin{align*}
\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & 1-\sqrt{2} & \cdots & 1+\sqrt{2} & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
$4>1+\sqrt{2}$ であるから,$x\geqq4$ のとき,$f'(x)>0$ となり $f(x)$ は単調に増加するから\begin{array}{|c||c|c|c|c|c|}\hline
x & \cdots & 1-\sqrt{2} & \cdots & 1+\sqrt{2} & \cdots \\\hline
f'(x) & + & 0 & – & 0 & + \\\hline
f(x) & \nearrow & 極大 & \searrow & 極小 & \nearrow \\\hline
\end{array}
\end{align*}
\begin{align*}
f(x)&\geqq f(4) \\[4pt]
&=64-48-12-1 \\[4pt]
&=3>0
\end{align*}
したがって,$x^3>3x^2+3x+1$ が成り立つ。f(x)&\geqq f(4) \\[4pt]
&=64-48-12-1 \\[4pt]
&=3>0
\end{align*}
2003年 富山大
2003年 富山大正の定数 $a$ に対して $f(x)=ax^2+a(a-3)x+1$ とおく。$x\geqq0$ のとき,$f(x)\geqq0$ であることを証明せよ。
【解答と考え方】
$x\geqq0$ における $f(x)$ の最小値が0以上であることを示そう。まずは平方完成して頂点の $x$ 座標(軸の位置)を調べよう。
(i) $-\dfrac{a-3}{2}<0$ すなわち $a>3$ のとき
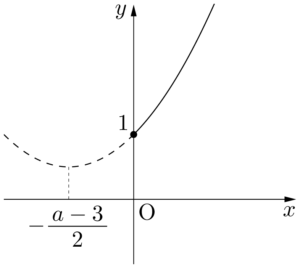
$f(x)$ は $x=0$ のとき最小値1をとるから,$f(x)\geqq0$ は成り立つ。
(ii) $-\dfrac{a-3}{2}\geqq0$ すなわち $0<a\leqq3$ のとき

$f(x)$ は $x=-\dfrac{a-3}{2}$ のとき最小値 $-\dfrac{a(a-3)^2}{4}+1$ をとる。ここで,$g(a)=-\dfrac{a(a-3)^2}{4}+1$ とおくと,
したがって,$g(a)\geqq0$ となるから $f(x)\geqq0$ が成り立つ。
(i),(ii)より,$x\geqq0$ のとき,$f(x)\geqq0$ が成り立つ。
$x\geqq0$ における $f(x)$ の最小値が0以上であることを示そう。まずは平方完成して頂点の $x$ 座標(軸の位置)を調べよう。
\begin{align*}
f(x)=a\left(x+\dfrac{a-3}{2}\right)^2-\dfrac{a(a-3)^2}{4}+1
\end{align*}
$y=f(x)$ の頂点の $x$ 座標は $-\dfrac{a-3}{2}$ であることが分かる。軸の位置で場合分けをして考える。f(x)=a\left(x+\dfrac{a-3}{2}\right)^2-\dfrac{a(a-3)^2}{4}+1
\end{align*}
(i) $-\dfrac{a-3}{2}<0$ すなわち $a>3$ のとき

$f(x)$ は $x=0$ のとき最小値1をとるから,$f(x)\geqq0$ は成り立つ。
(ii) $-\dfrac{a-3}{2}\geqq0$ すなわち $0<a\leqq3$ のとき

$f(x)$ は $x=-\dfrac{a-3}{2}$ のとき最小値 $-\dfrac{a(a-3)^2}{4}+1$ をとる。ここで,$g(a)=-\dfrac{a(a-3)^2}{4}+1$ とおくと,
\begin{align*} g'(a)&=-\dfrac{1}{4}\{(a-3)^2+2a(a-3)\} \\[4pt] &=-\dfrac{1}{4}(a-3)\{(a-3)+2a\} \\[4pt] &=-\dfrac{3}{4}(a-3)(a-1) \end{align*}
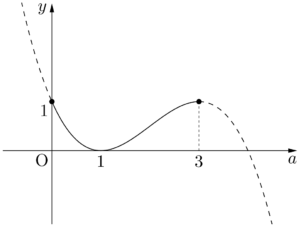
$g'(a)=0$ とすると,$a=1,~3$ よって,$g(a)$ の増減は次のようになる。\begin{align*} \begin{array}{|c||c|c|c|c|c|}\hline a & 0 & \cdots & 1 & \cdots & 3 \\\hline g'(a) & & – & 0 & + & \\\hline g(a) & & \searrow & 極小 & \nearrow & \\\hline \end{array} \end{align*}
$g(1)=0$ であるから,$y=g(a)$ のグラフは次のようになる。
したがって,$g(a)\geqq0$ となるから $f(x)\geqq0$ が成り立つ。
(i),(ii)より,$x\geqq0$ のとき,$f(x)\geqq0$ が成り立つ。




















