Contents
原点のまわりの回転

ヒロ
原点のまわりの回転移動を理解しよう。
座標平面上の点P $(a,~b)$ を原点のまわりに $\theta$ だけ回転させた点をQ$(X,~Y)$ とする。
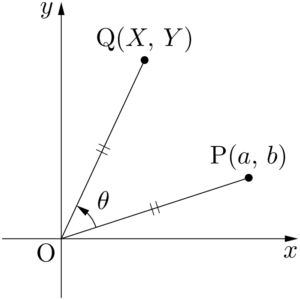
$\text{OP}=\sqrt{a^2+b^2}$ であるから,OPと $x$ 軸の正の方向となす角を $\alpha$ とすると,
\begin{align*}
\cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}},~\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}}~\cdots\cdots①
\end{align*}
が成り立つ。$\text{OP}=\text{OQ}$ であるから\cos\alpha=\dfrac{a}{\sqrt{a^2+b^2}},~\sin\alpha=\dfrac{b}{\sqrt{a^2+b^2}}~\cdots\cdots①
\end{align*}
\begin{align*}
&X=\sqrt{a^2+b^2}\cos(\alpha+\theta) \\[4pt]
&Y=\sqrt{a^2+b^2}\sin(\alpha+\theta)
\end{align*}
となる。加法定理と①を用いて変形すると,次のようになる。&X=\sqrt{a^2+b^2}\cos(\alpha+\theta) \\[4pt]
&Y=\sqrt{a^2+b^2}\sin(\alpha+\theta)
\end{align*}
\begin{align*}
X&=\sqrt{a^2+b^2}(\cos\alpha\cos\theta-\sin\alpha\sin\theta) \\[4pt]
&=\sqrt{a^2+b^2}\left(\dfrac{a}{\sqrt{a^2+b^2}}\cos\theta-\dfrac{b}{\sqrt{a^2+b^2}}\sin\theta\right) \\[4pt]
&=a\cos\theta-b\sin\theta \\[4pt]
Y&=\sqrt{a^2+b^2}(\sin\alpha\cos\theta+\cos\alpha\sin\theta) \\[4pt]
&=\sqrt{a^2+b^2}\left(\dfrac{b}{\sqrt{a^2+b^2}}\cos\theta+\dfrac{a}{\sqrt{a^2+b^2}}\sin\theta\right) \\[4pt]
&=b\cos\theta+a\sin\theta
\end{align*}
したがって,点P$(a,~b)$ を原点のまわりに $\theta$ だけ回転させた点Qの座標はX&=\sqrt{a^2+b^2}(\cos\alpha\cos\theta-\sin\alpha\sin\theta) \\[4pt]
&=\sqrt{a^2+b^2}\left(\dfrac{a}{\sqrt{a^2+b^2}}\cos\theta-\dfrac{b}{\sqrt{a^2+b^2}}\sin\theta\right) \\[4pt]
&=a\cos\theta-b\sin\theta \\[4pt]
Y&=\sqrt{a^2+b^2}(\sin\alpha\cos\theta+\cos\alpha\sin\theta) \\[4pt]
&=\sqrt{a^2+b^2}\left(\dfrac{b}{\sqrt{a^2+b^2}}\cos\theta+\dfrac{a}{\sqrt{a^2+b^2}}\sin\theta\right) \\[4pt]
&=b\cos\theta+a\sin\theta
\end{align*}
\begin{align*}
\text{Q}(a\cos\theta-b\sin\theta,~a\sin\theta+b\cos\theta)
\end{align*}
となる。\text{Q}(a\cos\theta-b\sin\theta,~a\sin\theta+b\cos\theta)
\end{align*}

ヒロ
この結果を公式として覚えると回転移動が楽にできる。
回転移動 点P$(a,~b)$ を原点のまわりに $\theta$ だけ回転させて点をQとすると
特に,$\theta=\dfrac{\pi}{2}$ のときは点Qの座標は $(-b,~a)$ となる。これは移動させる前の点Pの座標を入れ換えて,$x$ 座標の符号を変えれば良いことを表している。
\begin{align*}
\text{Q}(a\cos\theta-b\sin\theta,~a\sin\theta+b\cos\theta)
\end{align*}
となる。\text{Q}(a\cos\theta-b\sin\theta,~a\sin\theta+b\cos\theta)
\end{align*}
特に,$\theta=\dfrac{\pi}{2}$ のときは点Qの座標は $(-b,~a)$ となる。これは移動させる前の点Pの座標を入れ換えて,$x$ 座標の符号を変えれば良いことを表している。
原点以外の点のまわりの回転

ヒロ
原点以外の点のまわりの回転移動もできるようにしよう。
座標平面上の点P$(a,~b)$ を点R$(c,~d)$ のまわりに $\theta$ だけ回転させた点をQ$(X,~Y)$ とする。
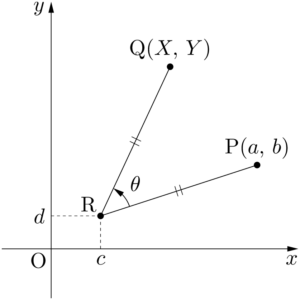
回転の中心Rが原点と重なるように,3点P,Q,Rを平行移動して考える。2点P,Qの平行移動後の点をそれぞれP$’$,Q$’$ とすると,
\begin{align*}
\text{P}'(a-c,~b-d),~\text{Q}'(X-c,~Y-d)
\end{align*}
となる。Q’はP’を原点のまわりに $\theta$ だけ回転した点であるから\text{P}'(a-c,~b-d),~\text{Q}'(X-c,~Y-d)
\end{align*}
\begin{align*}
&\begin{cases}
X-c=(a-c)\cos\theta-(b-d)\sin\theta \\[4pt]
Y-d=(a-c)\sin\theta+(b-d)\cos\theta
\end{cases}
\end{align*}
よって,求める点Qの座標は&\begin{cases}
X-c=(a-c)\cos\theta-(b-d)\sin\theta \\[4pt]
Y-d=(a-c)\sin\theta+(b-d)\cos\theta
\end{cases}
\end{align*}
\begin{align*}
\text{Q}((a-c)\cos\theta-(b-d)\sin\theta+c,~(a-c)\sin\theta+(b-d)\cos\theta+d)
\end{align*}
となる。\text{Q}((a-c)\cos\theta-(b-d)\sin\theta+c,~(a-c)\sin\theta+(b-d)\cos\theta+d)
\end{align*}

ヒロ
原点のまわりの回転移動を考えるように平行移動するのがポイント。


















