Contents
点を回転させる問題
2020年 慶應義塾大・薬$xy$ 平面上に点P$(9,~3)$ と点Q$(3,~1)$ がある。点Qを中心に,点Pを反時計回りに15°回転させた点をP$’$ とする。ただし,$\text{PQ}=\text{P}’\text{Q}$ である。このとき,点P$’$の座標を求めると,$x$ 座標は $\myhako$ である。
【考え方と解答】
点Qが原点と重なるように,2点P,Qを平行移動する。点Pの平行移動後の点をAとすると,A$(6,~2)$ となる。$\sin15\Deg$,$\cos15\Deg$ を求める。
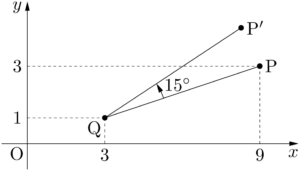
点Qが原点と重なるように,2点P,Qを平行移動する。点Pの平行移動後の点をAとすると,A$(6,~2)$ となる。$\sin15\Deg$,$\cos15\Deg$ を求める。
\begin{align*}
\sin15\Deg&=\sin(45\Deg-30\Deg) \\[4pt]
&=\sin45\Deg\cos30\Deg-\cos45\Deg\sin30\Deg \\[4pt]
&=\dfrac{\sqrt{2}}{2}\Cdota\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]
\cos15\Deg&=\cos(45\Deg-30\Deg) \\[4pt]
&=\cos45\Deg\cos30\Deg+\sin45\Deg\sin30\Deg \\[4pt]
&=\dfrac{\sqrt{2}}{2}\Cdota\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{\sqrt{6}+\sqrt{2}}{4}
\end{align*}
よって,点Aを原点のまわりに15°だけ回転させた点をA$'(X,~Y)$ とすると\sin15\Deg&=\sin(45\Deg-30\Deg) \\[4pt]
&=\sin45\Deg\cos30\Deg-\cos45\Deg\sin30\Deg \\[4pt]
&=\dfrac{\sqrt{2}}{2}\Cdota\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{2}}{2}\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]
\cos15\Deg&=\cos(45\Deg-30\Deg) \\[4pt]
&=\cos45\Deg\cos30\Deg+\sin45\Deg\sin30\Deg \\[4pt]
&=\dfrac{\sqrt{2}}{2}\Cdota\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{2}}{2}\Cdota\dfrac{1}{2} \\[4pt]
&=\dfrac{\sqrt{6}+\sqrt{2}}{4}
\end{align*}
\begin{align*}
X&=6\cos15\Deg-2\sin15\Deg \\[4pt]
&=6\Cdota\dfrac{\sqrt{6}+\sqrt{2}}{4}-2\Cdota\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]
&=\sqrt{6}+2\sqrt{2}
\end{align*}
原点と重なっている点Qが元の位置に戻るように,$x$ 軸方向に3,$y$ 軸方向に1だけ平行移動して,求める点P$’$ の $x$ 座標はX&=6\cos15\Deg-2\sin15\Deg \\[4pt]
&=6\Cdota\dfrac{\sqrt{6}+\sqrt{2}}{4}-2\Cdota\dfrac{\sqrt{6}-\sqrt{2}}{4} \\[4pt]
&=\sqrt{6}+2\sqrt{2}
\end{align*}
\begin{align*}
\sqrt{6}+2\sqrt{2}+3
\end{align*}
\sqrt{6}+2\sqrt{2}+3
\end{align*}


ヒロ
今回は $x$ 座標だけを求めたが,$y$ 座標を求めると $2\sqrt{6}-\sqrt{2}+1$ となる。
円を回転させる問題
2019年 兵庫県立大原点Oを中心とする半径1の定円 $C_0$ 上を,半径1の円 $C_1$ が外接しながらすべることなく回転するとき,$C_1$ 上の定点Pはある曲線を描く。Pのはじめの位置をA$(1,~0)$,また,$C_1$ の中心をQとして,以下の問に答えなさい。
(1) 円 $C_1$ が角 $\dfrac{\pi}{3}$ だけ回転したとき,すなわち,$\kaku{QOA}=\dfrac{\pi}{3}$ となったときの点Pの座標を求めなさい。
(2) 一般に,円 $C_1$ が角 $\theta~(0\leqq\theta\leqq2\pi)$ だけ回転したときの点Pの座標を $\theta$ を用いて表しなさい。
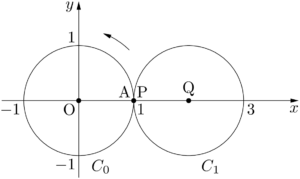
(1) 円 $C_1$ が角 $\dfrac{\pi}{3}$ だけ回転したとき,すなわち,$\kaku{QOA}=\dfrac{\pi}{3}$ となったときの点Pの座標を求めなさい。
(2) 一般に,円 $C_1$ が角 $\theta~(0\leqq\theta\leqq2\pi)$ だけ回転したときの点Pの座標を $\theta$ を用いて表しなさい。

【(1)の考え方と解答】
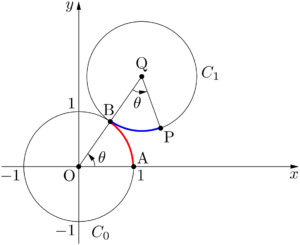
まず,点Qの座標を求める。$\kaku{QOA}=\dfrac{\pi}{3}$ と書かれているから,次の図を描くことができる。
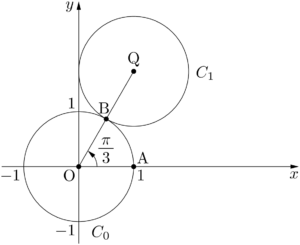
OQの長さは2であるから,点Qの座標を $(x,~y)$ とすると
円 $C_0$ 上を円 $C_1$ が外接しながらすべらずに回転しているから,$\ko{AB}$ の長さと $\ko{PB}$ の長さは等しい。2円の半径が等しいから,$\kaku{QBP}=\dfrac{\pi}{3}$ となる。
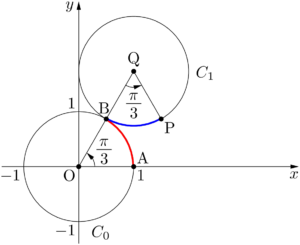
したがって,点Pは点Bを点Qを中心に $\dfrac{\pi}{3}$ だけ回転させた点である。点BはOQの中点であるから,B$\left(\dfrac{1}{2},~\dfrac{\sqrt{3}}{2}\right)$ となる。
2点B,Qを点Qが原点に重なるように平行移動させる。点Bの移動後の点をB$’$ とすると,B$’\left(-\dfrac{1}{2},~-\dfrac{\sqrt{3}}{2}\right)$ となる。原点を中心に点B$’$ を $\dfrac{\pi}{3}$ だけ回転させた点の座標を $(x,~y)$ とすると
まず,点Qの座標を求める。$\kaku{QOA}=\dfrac{\pi}{3}$ と書かれているから,次の図を描くことができる。

OQの長さは2であるから,点Qの座標を $(x,~y)$ とすると
\begin{align*}
&x=2\cos\dfrac{\pi}{3}=1 \\[4pt]
&y=2\sin\dfrac{\pi}{3}=\sqrt{3}
\end{align*}
となり,Q$(1,~\sqrt{3})$ であることが分かる。次に点Pの位置を考える。&x=2\cos\dfrac{\pi}{3}=1 \\[4pt]
&y=2\sin\dfrac{\pi}{3}=\sqrt{3}
\end{align*}
円 $C_0$ 上を円 $C_1$ が外接しながらすべらずに回転しているから,$\ko{AB}$ の長さと $\ko{PB}$ の長さは等しい。2円の半径が等しいから,$\kaku{QBP}=\dfrac{\pi}{3}$ となる。

したがって,点Pは点Bを点Qを中心に $\dfrac{\pi}{3}$ だけ回転させた点である。点BはOQの中点であるから,B$\left(\dfrac{1}{2},~\dfrac{\sqrt{3}}{2}\right)$ となる。
2点B,Qを点Qが原点に重なるように平行移動させる。点Bの移動後の点をB$’$ とすると,B$’\left(-\dfrac{1}{2},~-\dfrac{\sqrt{3}}{2}\right)$ となる。原点を中心に点B$’$ を $\dfrac{\pi}{3}$ だけ回転させた点の座標を $(x,~y)$ とすると
\begin{align*}
x&=-\dfrac{1}{2}\cos\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2}\sin\dfrac{\pi}{3} \\[4pt]
&=-\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{1}{2} \\[4pt]
y&=-\dfrac{1}{2}\sin\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{2}\cos\dfrac{\pi}{3} \\[4pt]
&=-\dfrac{\sqrt{3}}{4}-\dfrac{3}{4}=-\dfrac{\sqrt{3}}{2}
\end{align*}
となるから,この点を $x$ 軸方向に1,$y$ 軸方向に $\sqrt{3}$ だけ平行移動して,求める点Pの座標は,P$\left(\dfrac{3}{2},~\dfrac{\sqrt{3}}{2}\right)$x&=-\dfrac{1}{2}\cos\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2}\sin\dfrac{\pi}{3} \\[4pt]
&=-\dfrac{1}{4}+\dfrac{3}{4}=\dfrac{1}{2} \\[4pt]
y&=-\dfrac{1}{2}\sin\dfrac{\pi}{3}-\dfrac{\sqrt{3}}{2}\cos\dfrac{\pi}{3} \\[4pt]
&=-\dfrac{\sqrt{3}}{4}-\dfrac{3}{4}=-\dfrac{\sqrt{3}}{2}
\end{align*}
(2) 一般に,円 $C_1$ が角 $\theta~(0\leqq\theta\leqq2\pi)$ だけ回転したときの点Pの座標を $\theta$ を用いて表しなさい。
【(2)の考え方と解答】
角が具体的に定められた(1)を解くことによって「考え方」を理解することで,(2)も解きやすくなるだろう。
2点B,Qの座標はそれぞれ $(\cos\theta,~\sin\theta)$,$(2\cos\theta,~2\sin\theta)$ である。点Qが原点と重なるように平行移動する。平行移動後,点Bが点B$’$ に移るとすると,B$'(-\cos\theta,~-\sin\theta)$ である。点B$’$ を原点のまわりに $\theta$ だけ回転した点をP$'(x,~y)$ とすると
角が具体的に定められた(1)を解くことによって「考え方」を理解することで,(2)も解きやすくなるだろう。

2点B,Qの座標はそれぞれ $(\cos\theta,~\sin\theta)$,$(2\cos\theta,~2\sin\theta)$ である。点Qが原点と重なるように平行移動する。平行移動後,点Bが点B$’$ に移るとすると,B$'(-\cos\theta,~-\sin\theta)$ である。点B$’$ を原点のまわりに $\theta$ だけ回転した点をP$'(x,~y)$ とすると
\begin{align*}
x&=-\cos\theta\Cdota\cos\theta+\sin\theta\Cdota\sin\theta \\[4pt]
&=-\cos^2\theta+\sin^2\theta \\[4pt]
y&=-\cos\theta\sin\theta-\sin\theta\cos\theta \\[4pt]
&=-2\sin\theta\cos\theta
\end{align*}
点P$’$ を $x$ 軸方向に $2\cos\theta$,$y$ 軸方向に $2\sin\theta$ だけ平行移動した点がPであるから,求める点Pの座標は次のようになる。x&=-\cos\theta\Cdota\cos\theta+\sin\theta\Cdota\sin\theta \\[4pt]
&=-\cos^2\theta+\sin^2\theta \\[4pt]
y&=-\cos\theta\sin\theta-\sin\theta\cos\theta \\[4pt]
&=-2\sin\theta\cos\theta
\end{align*}
\begin{align*}
\text{P}(2\cos\theta-\cos^2\theta+\sin^2\theta,~2\sin\theta-2\sin\theta\cos\theta)
\end{align*}
\text{P}(2\cos\theta-\cos^2\theta+\sin^2\theta,~2\sin\theta-2\sin\theta\cos\theta)
\end{align*}
双曲線を回転させる問題
2006年 早稲田大$xy$ 平面上の曲線 $x^2-y^2=2$ を,原点を中心として反時計回りに $\dfrac{\pi}{4}$ 回転した曲線を $G$ とする。曲線 $G$ の方程式を求めよ。

ヒロ
「曲線上の動点に連動する点の軌跡」の記事で説明した方法で考えよう。
【考え方と解答】
曲線 $x^2-y^2=2$ 上の点P$(s,~t)$ を原点を中心として反時計回りに $\dfrac{\pi}{4}$ 回転した点をQ$(X,~Y)$ とする。点Pは点Qを原点を中心として $-\dfrac{\pi}{4}$ 回転した点であるから
したがって,曲線 $G$ の方程式は $xy=1$
曲線 $x^2-y^2=2$ 上の点P$(s,~t)$ を原点を中心として反時計回りに $\dfrac{\pi}{4}$ 回転した点をQ$(X,~Y)$ とする。点Pは点Qを原点を中心として $-\dfrac{\pi}{4}$ 回転した点であるから
\begin{align*}
s&=X\cos\left(-\dfrac{\pi}{4}\right)-Y\sin\left(-\dfrac{\pi}{4}\right) \\[4pt]
&=\dfrac{X+Y}{\sqrt{2}} \\[4pt]
t&=X\sin\left(-\dfrac{\pi}{4}\right)+Y\cos\left(-\dfrac{\pi}{4}\right) \\[4pt]
&=\dfrac{-X+Y}{\sqrt{2}}
\end{align*}
点Pは曲線 $x^2-y^2=2$ 上の点であるからs&=X\cos\left(-\dfrac{\pi}{4}\right)-Y\sin\left(-\dfrac{\pi}{4}\right) \\[4pt]
&=\dfrac{X+Y}{\sqrt{2}} \\[4pt]
t&=X\sin\left(-\dfrac{\pi}{4}\right)+Y\cos\left(-\dfrac{\pi}{4}\right) \\[4pt]
&=\dfrac{-X+Y}{\sqrt{2}}
\end{align*}
\begin{align*}
&s^2-t^2=2 \\[4pt]
&\left(\dfrac{X+Y}{\sqrt{2}}\right)^2-\left(\dfrac{-X+Y}{\sqrt{2}}\right)^2=2 \\[4pt]
&\dfrac{2Y\Cdot2X}{2}=2 \\[4pt]
&XY=1
\end{align*}
これは点Qが曲線 $xy=1$ 上にあることを示している。&s^2-t^2=2 \\[4pt]
&\left(\dfrac{X+Y}{\sqrt{2}}\right)^2-\left(\dfrac{-X+Y}{\sqrt{2}}\right)^2=2 \\[4pt]
&\dfrac{2Y\Cdot2X}{2}=2 \\[4pt]
&XY=1
\end{align*}
したがって,曲線 $G$ の方程式は $xy=1$



















