Contents
半径と中心間距離の関係式

ヒロ
2つの円の位置関係に応じて,2つの円の半径と中心間の距離の関係式を表せるようにしよう。
2つの円を $C_1,~C_2$ とし,それぞれの半径を $r_1,~r_2$,中心間の距離を $d$ とする。
理解しやすいのは,2つの円が外接するときだろう。下図のようになっていることから,2つの円が外接するときは
\begin{align*}
r_1+r_2=d
\end{align*}
が成り立つことが分かる。r_1+r_2=d
\end{align*}
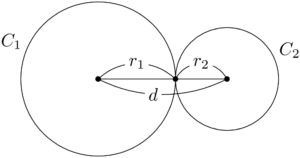
この状態から,2つの円の中心間距離を長くすると,2つの円は共有点をもたなくなり「2つの円は離れている」状態になる。このとき,$d$ の値は,2つの円の半径の和より大きくなるから,
\begin{align*}
r_1+r_2<d \end{align*}
となる。r_1+r_2<d \end{align*}
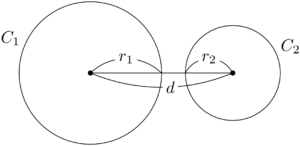
次に,2つの円が内接するときを考える。下図の状態から,
\begin{align*} r_1-r_2=d \end{align*}
が成り立つ。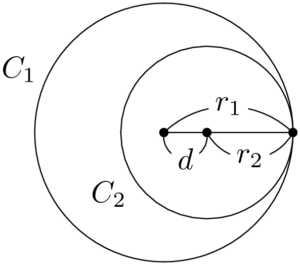
ただし,上の図は $r_1>r_2$ の場合の様子を描いたものである。半径の大小関係が分からないときは,左辺を「2つの円の半径の差」にすればよいから,絶対値記号を使うことで表せる。つまり,2つの円が内接するときは
\begin{align*} \abs{r_1-r_2}=d \end{align*}
が成り立つ。2つの円が内接している上図の状態から,$r_1$ と $r_2$ の値を変えずに,$d$ の値を小さくすると,2つの円は近づいて共有点をもたなくなる。つまり「一方が他方の内部にある」状態になる。下図から
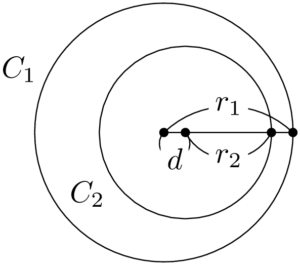
2つの円の半径の大小関係が定まっていない場合にも対応できるようにすると,左辺を「2つの円の半径の差」にすればよいから,
\begin{align*} r_1-r_2>d \end{align*}
が成り立つことが分かる。
2つの円の半径の大小関係が定まっていない場合にも対応できるようにすると,左辺を「2つの円の半径の差」にすればよいから,
\begin{align*} \abs{r_1-r_2}>d \end{align*}
となる。また,中心間の距離 $d$ は正であるから,それを合わせると \begin{align*} 0<d<\abs{r_1-r_2} \end{align*}
となる。最後に下図のように「2つの円が2点で交わる」ときの説明をする。
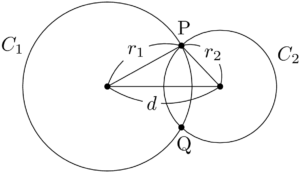
上図の状態になるためには,下図のような外接している状態から,2つの円の半径を変えずに,中心間距離を小さくすればよいことが分かる。
ただし,中心間距離を小さくし過ぎると,下図のように内接する状態になってしまうから,$d$ は内接するときの中心間距離より大きくしなければならない。
以上のことから,2つの円が2点で交わるときは
\begin{align*} \abs{r_1-r_2}<d<r_1+r_2 \end{align*}
が成り立つことが分かる。この考え方以外に,三角形の成立条件を考える方法がある。2つの円 $C_1,~C_2$ の中心をそれぞれC,Dとして,$\sankaku{CDP}$ に着目する。
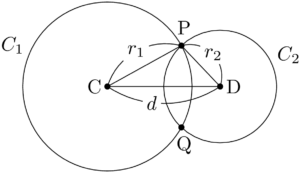
$\sankaku{CDP}$ の3辺の長さが $r_1,~r_2,~d$ であるから,三角形の成立条件を考えることでも
\begin{align*} \abs{r_1-r_2}<d<r_1+r_2 \end{align*}
を導くことができる。
2つの円の位置関係に関する問題【千葉工業大】
2012年 千葉工業大円 $x^2+y^2=9$ と円 $x^2+(y+a)^2=9$ が共有点をもつような定数 $a$ の値の範囲は
\begin{align*}
\myhako\leqq a\leqq\myhako
\end{align*}
である。\myhako\leqq a\leqq\myhako
\end{align*}
【考え方と解答】
2つの円が共有点をもつのは,
円 $x^2+y^2=9$ の中心は原点で,半径は3である。また,円 $x^2+(y+a)^2=9$ の中心は $(0,~-a)$ で,半径は3である。
したがって
2つの円が共有点をもつのは,
\begin{align*}
(半径の差)\leqq(中心間の距離)\leqq(半径の和)
\end{align*}
となるときである。(半径の差)\leqq(中心間の距離)\leqq(半径の和)
\end{align*}
円 $x^2+y^2=9$ の中心は原点で,半径は3である。また,円 $x^2+(y+a)^2=9$ の中心は $(0,~-a)$ で,半径は3である。
したがって
\begin{align*}
&3-3\leqq\abs{a}\leqq3+3 \\[4pt]
&0\leqq\abs{a}\leqq6 \\[4pt]
&-6\leqq a\leqq6
\end{align*}
&3-3\leqq\abs{a}\leqq3+3 \\[4pt]
&0\leqq\abs{a}\leqq6 \\[4pt]
&-6\leqq a\leqq6
\end{align*}

ヒロ
この問題では「2点で交わる」とは書かれておらず,単に「共有点をもつ」と書かれているだけだから,外接するときや内接するときも含まれることに注意しよう。


















