Contents
2つの円の位置関係に関する問題【秋田大】
2020年 秋田大座標平面上において,次の問いに答えなさい。
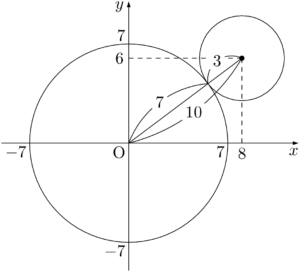
(1) 点$(8,~6)$を中心とし,円 $x^2+y^2=49$ に外接する円の方程式を求めなさい。
(2) $k$ を実数とし,2つの円 $x^2+y^2-4x+4ky+4k^2-5=0$,$x^2+y^2=49$ が共有点をもたないとき,定数 $k$ のとりうる値の範囲を求めなさい。
(1) 点$(8,~6)$を中心とし,円 $x^2+y^2=49$ に外接する円の方程式を求めなさい。
(2) $k$ を実数とし,2つの円 $x^2+y^2-4x+4ky+4k^2-5=0$,$x^2+y^2=49$ が共有点をもたないとき,定数 $k$ のとりうる値の範囲を求めなさい。
【(1)の考え方と解答】
2つの円が外接するとき,2つの円の半径の和が中心間距離 $d$ と等しい。
求める円の半径を $r$ とすると,$r+7=d$ であるから
2つの円が外接するとき,2つの円の半径の和が中心間距離 $d$ と等しい。
\begin{align*}
d&=\sqrt{8^2+6^2}=10
\end{align*}
この計算については,真面目に計算しても良いが,$3:4:5$ の有名直角三角形を考えることで,瞬時に10になることが分かるようにしよう。d&=\sqrt{8^2+6^2}=10
\end{align*}
求める円の半径を $r$ とすると,$r+7=d$ であるから
\begin{align*}
&r+7=10 \\[4pt]
&r=3
\end{align*}
したがって,求める円の方程式は&r+7=10 \\[4pt]
&r=3
\end{align*}
\begin{align*}
(x-8)^2+(y-6)^2=9
\end{align*}
(x-8)^2+(y-6)^2=9
\end{align*}

(2) $k$ を実数とし,2つの円 $x^2+y^2-4x+4ky+4k^2-5=0$,$x^2+y^2=49$ が共有点をもたないとき,定数 $k$ のとりうる値の範囲を求めなさい。
【(2)の考え方と解答】
2つの円が共有点をもたないとき,2つの円が離れているときと一方が他方の内部にあるときがある。
円 $x^2+y^2=49$ の中心は原点であり,半径は7である。また,$x^2+y^2-4x+4ky+4k^2-5=0$ より
2つの円の中心間の距離を $d$ とすると
中心間の距離が2つの円の半径の和より長いから,$d>3+7=10$ より
中心間の距離が2つの円の半径の差より短いから,$0<d<7-3=4$ より
2つの円が共有点をもたないとき,2つの円が離れているときと一方が他方の内部にあるときがある。
円 $x^2+y^2=49$ の中心は原点であり,半径は7である。また,$x^2+y^2-4x+4ky+4k^2-5=0$ より
\begin{align*}
&(x-2)^2+(y+2k)^2=9
\end{align*}
となるから,この円の中心は $(2,~-2k)$ であり,半径は3である。&(x-2)^2+(y+2k)^2=9
\end{align*}
2つの円の中心間の距離を $d$ とすると
\begin{align*}
d&=\sqrt{2^2+(-2k)^2}=2\sqrt{k^2+1}
\end{align*}
(i) 2つの円が離れているときd&=\sqrt{2^2+(-2k)^2}=2\sqrt{k^2+1}
\end{align*}
中心間の距離が2つの円の半径の和より長いから,$d>3+7=10$ より
\begin{align*}
&2\sqrt{k^2+1}>10 \\[4pt]
&\sqrt{k^2+1}>5
\end{align*}
両辺を2乗すると&2\sqrt{k^2+1}>10 \\[4pt]
&\sqrt{k^2+1}>5
\end{align*}
\begin{align*}
&k^2+1>25 \\[4pt]
&k^2>24 \\[4pt]
&k<-2\sqrt{6},~2\sqrt{6}<k~\cdots\cdots① \end{align*}
(ii) 一方が他方の内部にあるとき&k^2+1>25 \\[4pt]
&k^2>24 \\[4pt]
&k<-2\sqrt{6},~2\sqrt{6}<k~\cdots\cdots① \end{align*}
中心間の距離が2つの円の半径の差より短いから,$0<d<7-3=4$ より
\begin{align*} &0<2\sqrt{k^2+1}<4 \\[4pt] &\sqrt{k^2+1}<2 \end{align*}
両辺を2乗して \begin{align*} &k^2+1<4 \\[4pt] &k^2<3 \\[4pt] &-\sqrt{3}<k<\sqrt{3}~\cdots\cdots② \end{align*}
①または②より,求める $k$ の値の範囲は \begin{align*} k<-2\sqrt{6},~-\sqrt{3}<k<\sqrt{3},~2\sqrt{6}<k \end{align*}

ヒロ
同値変形を利用した解法を説明しておく。
【同値変形を利用した別の考え方と解答】
\begin{align*}
&x^2+y^2-4x+4ky+4k^2-5=0~\cdots\cdots① \\[4pt]
&x^2+y^2=49~\cdots\cdots②
\end{align*}
とする。&x^2+y^2-4x+4ky+4k^2-5=0~\cdots\cdots① \\[4pt]
&x^2+y^2=49~\cdots\cdots②
\end{align*}
$②-①$ より
\begin{align*} &4x-4ky-4k^2-44=0 \\[4pt] &x-ky-k^2-11=0~\cdots\cdots③ \end{align*}
ここで「①かつ②」と「②かつ③」は同値であることを理解しよう。
③は①と②から作られた式であるから,「①かつ②」$\Longrightarrow$「②かつ③」が成り立つことは理解できるはず。
次に,$②-③\times4$ を計算すると①になるから,「②かつ③」$\Longrightarrow$「①かつ②」も成り立つことが分かる。
したがって,「①かつ②」と「②かつ③」は同値である。つまり,「円①と円②が共有点をもたない」条件は「円②と直線③が共有点をもたない」条件に言い換えることができる。
さらに「円②の中心と直線③との距離が円②の半径より大きい」と言い換えることができるから
\begin{align*} &\dfrac{\abs{-k^2-11}}{\sqrt{1^2+k^2}}>7 \\[4pt] &\abs{k^2+11}>7\sqrt{k^2+1} \end{align*}
両辺を2乗すると\begin{align*} &(k^2+11)^2>49(k^2+1) \\[4pt] &k^4-27k^2+72>0 \\[4pt] &(k^2-3)(k^2-24)>0 \\[4pt] &k^2<3,~24<k^2 \\[4pt] &-\sqrt{3}<k<\sqrt{3},~k<-2\sqrt{6},~2\sqrt{6}<k \end{align*}

ヒロ
ちなみに「①かつ②」と「①かつ③」も同値である。上の説明で①ではなく②を使ったのは,①を使うより計算が楽になるからである。

ヒロ
2つの円の位置関係と,中心間の距離と半径の関係式を自由に行き来できるようにしよう。

ヒロ
また,同値変形を意識することで,最後に説明した「同値変形を利用した解法」も使えるようになるため,解法の引き出しが多くなるだろう。


















