Contents
平行四辺形の頂点の座標【獨協医科大】
2007年 獨協医科大$xy$ 平面上に3点 $(-2,~0)$, $(4,~6)$, $(2,~-4)$ がある。この3点を頂点とする平行四辺形の残りの1頂点となり得る点は,$y$ 座標が大きい方から順に $\left(\myhako,~\myhako\right)$, $\left(\myhako,~\myhako\right)$, $\left(\myhako,~\myhako\right)$ である。
【考え方と解答】
この問題では,求めるべき点が3つあることが初めから分かっているが,中には点をいくつ求めるのか分かっていない問題もある。一般的に,平面上に3点が与えられているときに,その3点を頂点とする平行四辺形の残りの頂点は3つあることは常識にしておこう。
与えられている3点をA,B,Cとして図示すると次のようになる。
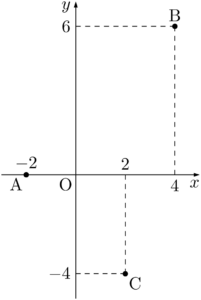
四角形ABPC,四角形ACBQ,四角形ABCRが平行四辺形になる3点P,Q,Rを求める。点Pは次のような位置にある。
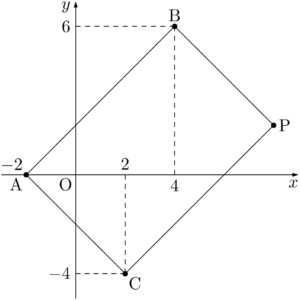
中学生なら次のようにして求めるだろう。
ACとBPが平行だから,AからCへ移動する方法を確認する。点Aから右に4,下に4移動すると点Cになるから,点Bからも同じように移動して,P$(8,~2)$ となる。次に点Qの座標を求める。
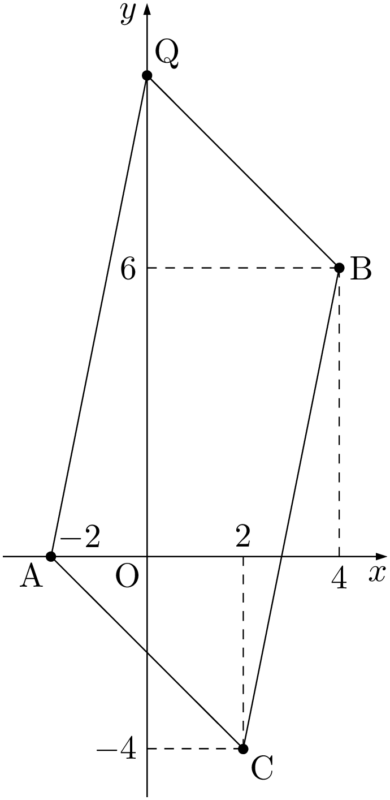
CからAに移動するには,左に4,上に4移動すれば良いから,点Bからも同じように移動すると,Q$(0,~10)$ であることが分かる。最後に点Rの座標を求める。
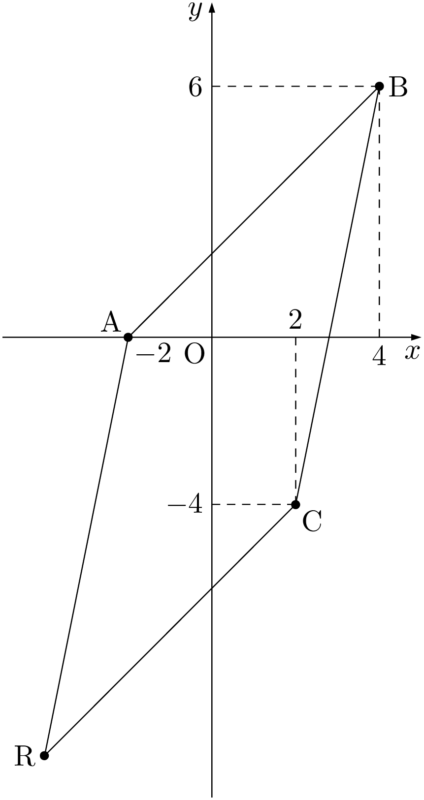
BからAへ移動するには,左に6,下に6移動すれば良いから,点Cからも同じように移動すると,R$(-4,~-10)$ であることが分かる。
この問題では,求めるべき点が3つあることが初めから分かっているが,中には点をいくつ求めるのか分かっていない問題もある。一般的に,平面上に3点が与えられているときに,その3点を頂点とする平行四辺形の残りの頂点は3つあることは常識にしておこう。
与えられている3点をA,B,Cとして図示すると次のようになる。

四角形ABPC,四角形ACBQ,四角形ABCRが平行四辺形になる3点P,Q,Rを求める。点Pは次のような位置にある。

中学生なら次のようにして求めるだろう。
ACとBPが平行だから,AからCへ移動する方法を確認する。点Aから右に4,下に4移動すると点Cになるから,点Bからも同じように移動して,P$(8,~2)$ となる。次に点Qの座標を求める。

CからAに移動するには,左に4,上に4移動すれば良いから,点Bからも同じように移動すると,Q$(0,~10)$ であることが分かる。最後に点Rの座標を求める。

BからAへ移動するには,左に6,下に6移動すれば良いから,点Cからも同じように移動すると,R$(-4,~-10)$ であることが分かる。

ヒロ
解き方にこだわらなければ,この程度の問題であれば,上で説明したように誰でも解けるはずである。

ヒロ
これを「点の座標を求めるときは文字で置こう!そして平行四辺形の対角線は中点で交わることを利用するんだ!」と言って,そのまま意味も分からずその通りの解き方を覚えて,それしかできなくなるようでは「すべて丸暗記」から抜け出すことはできないだろう。

ヒロ
とりあえず,その方法の解答も載せておく。
【別の考え方と解答】
求める点の座標をP$(x,~y)$ とおく。
(i) 四角形ABPCが平行四辺形になるとき
APとBCの中点が一致するから
CPとABの中点が一致するから
BPとACの中点が一致するから
求める点の座標をP$(x,~y)$ とおく。
(i) 四角形ABPCが平行四辺形になるとき
APとBCの中点が一致するから
\begin{align*}
&\dfrac{x-2}{2}=\dfrac{4+2}{2},~\dfrac{y+0}{2}=\dfrac{6-4}{2} \\[4pt]
&x=8,~y=2
\end{align*}
(ii) 四角形ACBPが平行四辺形になるとき&\dfrac{x-2}{2}=\dfrac{4+2}{2},~\dfrac{y+0}{2}=\dfrac{6-4}{2} \\[4pt]
&x=8,~y=2
\end{align*}
CPとABの中点が一致するから
\begin{align*}
&\dfrac{x+2}{2}=\dfrac{-2+4}{2},~\dfrac{y-4}{2}=\dfrac{0+6}{2} \\[4pt]
&x=0,~y=10
\end{align*}
(iii) 四角形ABCPが平行四辺形になるとき&\dfrac{x+2}{2}=\dfrac{-2+4}{2},~\dfrac{y-4}{2}=\dfrac{0+6}{2} \\[4pt]
&x=0,~y=10
\end{align*}
BPとACの中点が一致するから
\begin{align*}
&\dfrac{x+4}{2}=\dfrac{-2+2}{2},~\dfrac{y+6}{2}=\dfrac{0-4}{2} \\[4pt]
&x=-4,~y=-10
\end{align*}
以上より,求める点の座標は&\dfrac{x+4}{2}=\dfrac{-2+2}{2},~\dfrac{y+6}{2}=\dfrac{0-4}{2} \\[4pt]
&x=-4,~y=-10
\end{align*}
\begin{align*}
(8,~2),~(0,~10),~(-4,~-10)
\end{align*}
(8,~2),~(0,~10),~(-4,~-10)
\end{align*}


















