場合の数を求める問題を見るとすぐに「どの公式を使うのか?」を考える人が多いのですが,根本的に間違っています。
中学生のときは「公式を知らないから」かもしれませんが,1つずつ書き出したり,樹形図や表を利用して場合の数を求めていたはずです。
それが高校生になって,公式化され始めると,どの公式を使うのかを最初に考えるようになってしまいます。
そんなことでは場合の数・確率の問題において強くなるはずがありません。
そもそも考える順番が逆です。
樹形図を書いている途中や,書き始めた途端,または書こうとした直後に「これなら計算で求めることができる」と分かるから「数学が得意な人は少し考えただけで公式がスラスラ出てきていいなぁ」なんてトンチンカンなことを言い始めるのです。
問題を見たときに「さて・・・この問題はどの公式を使おうかな」なんて考えたことはありません。
問題の意味を捉えて,しっかり考えることで解く癖をつけるようにしましょう。
場合の数を求める問題

それでは実際に定期テストで出題された問題を解いてみよう。
(1) すべての部分集合の個数を求めよ。
(2) 要素 $a$ を含む部分集合の個数を求めよ。

次の記事で部分集合を書く問題を解いたけど,これは部分集合の個数を求める問題。
また,要素が1個の部分集合の具体例は $\{a\}$ である。
このように部分集合の個数で分類して考えると「現時点で分からないこと」が分かる。
要素が1個の部分集合は,さっき考えた $a$ だけを含むものや $b$ だけを含むものがある。つまり全部で6個あることが分かる。
次に要素が2個の部分集合を考えると,$\{a,~b\}$ や $\{a,~c\}$ と考えていくのでは,結局,部分集合をすべて書き出すことになり,これは大変だということが分かる。
「異なる6個のものから異なる2個を選ぶ方法が何通りあるのか」をすぐに計算できる方法を知っていればそれで良いが,現時点では知らないので,この考え方では大変だということ。
では,どうするのかということになるわけで,それぞれの要素について部分集合に入れるか入れないかを決めていくという方法で部分集合の個数を求めよう。
6つの要素に対して,部分集合に入れる場合は○印を付けて,入れない場合は×印を付けるというルールにする。
$(a,~b,~c,~d,~e,~f)=(○,~○,~×,~×,~○,~×)$ となっている場合は $\{a,~b,~e\}$ を表す。
すべてが×になったときは空集合 $\emptyset$ を表すし,すべてが○になったときは集合 $A$ を表す。
要素 $a$ に対しては○か×かの2通りの選択肢がある。その各々に対して要素 $b$ に対しても○か×かの2通りの選択肢がある。
また,その1つ1つの選択肢に対しても要素 $c$ も○か×かの2通りの選択肢がある。このように続けていくと,全部で6つの要素があるから,全部で
2\times2\times2\times2\times2\times2=2^6=64~通り
\end{align*}
(2) 要素 $a$ を含む部分集合の個数を求めよ。

(2)では要素 $a$ を含むことが決まっているから残りの要素について考えよう。
$a$ 以外の5つの要素に対して,部分集合に入れるか入れないかを考えて,求める部分集合の個数は
2\times2\times2\times2\times2=2^5=32~個
\end{align*}
場合の数を求める問題2

次も定期テストで出題された問題。

整数を作る問題では,どの位から考えるのかが重要で,次のポイントを覚えておこう。

今回の場合は百の位から考えよう。理由は・・・

問題文に「3桁の整数」とあるため,百の位の数字は0以外という条件が発生する。

十の位や一の位にはこのような条件はないため,百の位が最も条件が厳しい位ということになるね。
まず百の位の数字は1, 2, 3, 4, 5の5通りある。
そのそれぞれに対して,十の位の数字の決め方が百の位で使った数字以外の5通りある。
さらにそのそれぞれに対して,一の位の数字の決め方が残りの数字の4通りある。
よって,求める個数は
5\times5\times4=100~個
\end{align*}

整数を作る問題は頻出なので,簡単な問題から慣れていって難しい問題も解けるようにしていこう。
場合の数を求める問題3

大学入試でも一筆書きの問題が出題されることがあるが,ここで基本的な問題を解いておこう。


具体的にいくつか一筆書きで描いてみよう。

実際に描くときに「何か」を決めているはず。
実際に一筆書きをしようとすると,次の2つを決めていることが分かる。
- 3つの輪の描く順番
- それぞれの輪の描く方向
点Aから出る3つの輪に $p,~q,~r$ と名前を付ける。
また,それぞれの輪の描く方向が時計回りか反時計回りかの2通りあり,それぞれ①,②と区別することにする。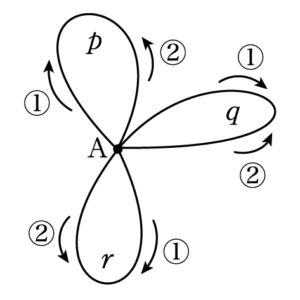
これで $p,~q,~r$ の順番とそれぞれに対して①,②を決めると,その決め方1つに対して一筆書きの方法が1つ決まる。
例えば,輪の描く順番を $p\to r\to q$ として,それぞれの書く方向を①②②とすると次の図ような一筆書きになる。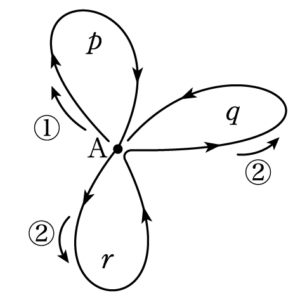
3つの輪の描く順番を考えると,最初に描く輪の決め方が3通りある。そのそれぞれに対して,2番目に描く輪は2通りある。最後に残った輪を描くから,輪の描く順番の決め方は $3\times2=6$ 通りある。
また,輪の描く方向の決め方はそれぞれの輪に対して2通りずつあるから,全部で $2\times2\times2=8$ 通りある。
したがって,一筆書きの方法は全部で
6\times8=48~通り
\end{align*}



















