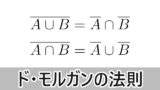ここでは条件の否定について説明します。
例えば「~は・・・です。」は肯定文と呼ばれます。
では否定文は「~は・・・ではない。」となりますね。
このように否定に書き換えるだけですが,文によっては書き換えることが難しいものもあります。
どのようなものでも否定を考えることができるようになりましょう。
条件の否定

ある条件 $p$ に対して「$p$ でない」というのも条件となる。このような条件の否定について理解しておこう。
また $\overline{\overline{p}}=p$ である。

条件の否定の例をいくつか挙げておこう。

$x$ を整数として「$x$ は偶数である」の否定は「$x$ は偶数でない」となるが,偶数でない整数は奇数であるから「$x$ は奇数である」となる。

否定の言葉を知っているとスムーズに言うことができる。
- 偶数と奇数
- 無理数と有理数
- $x=y$ と $x\neq y$
「すべて」を含む条件の否定

例えば日常会話に現れる例から考えてみよう。

「乃木坂46のメンバーは全員(すべて)可愛い。」の否定を考えよう。

これを「乃木坂46のメンバーは全員可愛くない。」としてしまったら大変なことになるね。

文全体を否定するわけだから「乃木坂46のメンバーは全員可愛いということはない。」が正しい否定になる。

この文の意味を噛み砕くと「乃木坂46のメンバーの中には可愛くない人もいる。」だ。

機械的に否定にするなら次のことを覚えておこう。

先程の例では「乃木坂46のあるメンバーは可愛くない。」という感じだ。

つまり「すべて」の否定は「少なくとも1つ存在する」となるとも言える。

数学の例で,さいころを3つ振ったときを考えてみよう。

「3つとも6の目が出る」の否定は「少なくとも1つは6でない目が出る」となる。

3つのさいころのうち,1つでも6でない目が出れば否定になっていることが分かるだろう。

また「すべての実数 $x$ に対して $x^2\geqq0$ である。」の否定は「ある実数 $x$ に対して $x^2<0$ である。」となる。
「ある」を含む条件の否定

それでは次に「ある」を含む条件の否定を理解しよう。

「乃木坂46のあるメンバーは歌が下手だ。」の否定を考えよう。

この否定を「乃木坂46のあるメンバーは歌が上手い。」なんて言わないように。

元の文を言い換えると「乃木坂46には歌が下手なメンバーが存在する。」となる。

ということは,この文の否定は「乃木坂46には歌が下手なメンバーなんていない」という意味になるのだから,「乃木坂46のすべてのメンバーは歌が上手い。」となる。

これも機械的にするなら次のことを覚えておこう。

数学の例で「ある実数 $x$ に対して $x^2<0$ である。」の否定は「すべての実数 $x$ に対して $x^2\geqq0$ である。」となる。

他には「$x,~y,~z$ のうち0であるものが存在する。」の否定は「$x,~y,~z$ はすべて0でない。」となる。
実際に出題された条件の否定に関する問題

それでは実際に定期テストに出題された問題を解いてみよう。
(1) $x$ は無理数である。
(2) $x<0$ (3) $x\neq1$
(4) $x=0$ かつ $y\neq0$
(5) $x\leqq0$ または $y\leqq0$
(6) $m,~n$ はともに奇数

「かつ」や「または」を含む条件の否定については,ド・モルガンの法則を利用しよう。

ド・モルガンの法則を利用できるようにしておこう。

また,「ともに~」の否定は「少なくとも一方が~」となることを機械的にできるようになると良いだろう。