Contents
2倍角を含む方程式
2019年 北里大$\cos x=\sin2t$,$0<x\leqq\dfrac{\pi}{2}$,$0\leqq t\leqq\dfrac{\pi}{2}$ を満たす2つの実数 $x,~t$ について考える。
(1) $x=\dfrac{\pi}{6}$ のとき,$t$ のとり得る値は $\myhako$ である。
(2) $x=t$ のとき,$t$ のとり得る値は $\myhako$ である。
(3) $x$ の各値に対して,$t$ がとり得る2つの値のうち,小さい方を $t_1$,大きい方を $t_2$ とする。このとき,$t_1$ は $x$ を用いて $t_1=\myhako\,x+\myhako$ と表される。
また,$\cos\left(x-\dfrac{t_1}{2}-\dfrac{t_2}{3}\right)$ の値が最大となるときの $x$ の値は $\myhako$ である。
(1) $x=\dfrac{\pi}{6}$ のとき,$t$ のとり得る値は $\myhako$ である。
(2) $x=t$ のとき,$t$ のとり得る値は $\myhako$ である。
(3) $x$ の各値に対して,$t$ がとり得る2つの値のうち,小さい方を $t_1$,大きい方を $t_2$ とする。このとき,$t_1$ は $x$ を用いて $t_1=\myhako\,x+\myhako$ と表される。
また,$\cos\left(x-\dfrac{t_1}{2}-\dfrac{t_2}{3}\right)$ の値が最大となるときの $x$ の値は $\myhako$ である。
【(1)の考え方と解答】
$x=\dfrac{\pi}{6}$ のとき,$\cos x=\dfrac{\sqrt{3}}{2}$ であるから,$\cos x=\sin2t$ より
$x=\dfrac{\pi}{6}$ のとき,$\cos x=\dfrac{\sqrt{3}}{2}$ であるから,$\cos x=\sin2t$ より
\begin{align*} \sin2t=\dfrac{\sqrt{3}}{2} \end{align*}
$0\leqq t\leqq\dfrac{\pi}{2}$ のとき,$0\leqq2t\leqq\pi$ であるから \begin{align*} &2t=\dfrac{\pi}{3},~\dfrac{2}{3}\pi \\[4pt] &t=\dfrac{\pi}{6},~\dfrac{\pi}{3} \end{align*}
(2) $x=t$ のとき,$t$ のとり得る値は $\myhako$ である。
【(2)の考え方と解答】
$x=t$ のとき,$\cos x=\sin2t$ より
$x=t$ のとき,$\cos x=\sin2t$ より
\begin{align*} &\cos t=\sin2t \\[4pt] &\cos t=2\sin t\cos t \\[4pt] &\cos t(2\sin t-1)=0 \\[4pt] &\cos t=0,~\sin t=\dfrac{1}{2} \end{align*}
$0\leqq t\leqq\dfrac{\pi}{2}$ より \begin{align*} t=\dfrac{\pi}{6},~\dfrac{\pi}{2} \end{align*}
(3) $x$ の各値に対して,$t$ がとり得る2つの値のうち,小さい方を $t_1$,大きい方を $t_2$ とする。このとき,$t_1$ は $x$ を用いて $t_1=\myhako\,x+\myhako$ と表される。
また,$\cos\left(x-\dfrac{t_1}{2}-\dfrac{t_2}{3}\right)$ の値が最大となるときの $x$ の値は $\myhako$ である。
【(3)の考え方と解答】
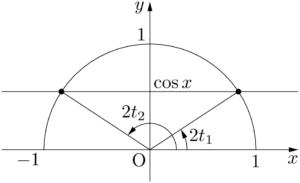
$0<x\leqq\dfrac{\pi}{2}$ のとき,$0\leqq\cos x<1$ であるから,$\cos x=\sin2t$ をみたす $2t_1,~2t_2$ は次のような角である。
ここで,$\cos x=\sin\left(\dfrac{\pi}{2}-x\right)$ であるから,$\cos x=\sin2t$ より
$0<x\leqq\dfrac{\pi}{2}$ のとき,$0\leqq\cos x<1$ であるから,$\cos x=\sin2t$ をみたす $2t_1,~2t_2$ は次のような角である。

ここで,$\cos x=\sin\left(\dfrac{\pi}{2}-x\right)$ であるから,$\cos x=\sin2t$ より
\begin{align*} \sin\left(\dfrac{\pi}{2}-x\right)=\sin2t \end{align*}
よって, \begin{align*} 2t=\dfrac{\pi}{2}-x~または~2t=\pi-\left(\dfrac{\pi}{2}-x\right) \end{align*}
$2t_1<2t_2$ であるから \begin{align*} &2t_1=\dfrac{\pi}{2}-x,~2t_2=\pi-\left(\dfrac{\pi}{2}-x\right) \\[4pt] &t_1=-\dfrac{1}{2}x+\dfrac{\pi}{4},~t_2=\dfrac{1}{2}x+\dfrac{\pi}{4} \end{align*}
この結果より \begin{align*} &\cos\left(x-\dfrac{t_1}{2}-\dfrac{t_2}{3}\right) \\[4pt] &=\cos\left\{x-\dfrac{1}{2}\left(-\dfrac{1}{2}x+\dfrac{\pi}{4}\right)-\dfrac{1}{3}\left(\dfrac{1}{2}x+\dfrac{\pi}{4}\right)\right\} \\[4pt] &=\cos\left(\dfrac{13}{12}x-\dfrac{5}{24}\pi\right) \end{align*}
$0<x\leqq\dfrac{\pi}{2}$ のとき, \begin{align*} -\dfrac{5}{24}\pi<\dfrac{13}{12}x-\dfrac{5}{24}\pi\leqq\dfrac{\pi}{3} \end{align*}
であるから,$\cos\left(x-\dfrac{t_1}{2}-\dfrac{t_2}{3}\right)$ の値が最大になるのは \begin{align*} \dfrac{13}{12}x-\dfrac{5}{24}\pi=0 \end{align*}
のときである。すなわち,$x=\dfrac{5}{26}\pi$ のときである。2倍角に関する最大最小問題
2020年 東洋大$3(\sin2\theta+\cos2\theta)\geqq\sqrt{2}$ であるとき,$\tan\theta$ がとりうる値の最小値は $\dfrac{\sqrt{\myhako}-\myhako}{\myhako}$,最大値は $\myhako-\sqrt{\myhako}$ である。
【考え方と解答】
不等式の角は $2\theta$ になっているが,求めるのは $\tan\theta$ の最大値と最小値であるから,$\theta$ に直して不等式を解こう。
$\theta=\dfrac{\pi}{2}+2n\pi$($n$ は整数)のとき,(*)は成り立たないから,$\theta\neq\dfrac{\pi}{2}+2n\pi$ である。すなわち $\cos\theta\neq0$ であるから,①の両辺を $\cos^2\theta>0$ で割って
不等式の角は $2\theta$ になっているが,求めるのは $\tan\theta$ の最大値と最小値であるから,$\theta$ に直して不等式を解こう。
\begin{align*}
3(\sin2\theta+\cos2\theta)\geqq\sqrt{2}~\cdots\cdots(*)
\end{align*}
とする。2倍角の公式より3(\sin2\theta+\cos2\theta)\geqq\sqrt{2}~\cdots\cdots(*)
\end{align*}
\begin{align*}
&3(2\sin\theta\cos\theta+\cos^2\theta-\sin^2\theta)\geqq\sqrt{2}~\cdots\cdots①
\end{align*}
両辺を $\cos^2\theta$ で割れば,$\tan\theta$ で表すことができる。$\cos\theta=0$ となるときは割ることができないことに注意して解き進めよう。&3(2\sin\theta\cos\theta+\cos^2\theta-\sin^2\theta)\geqq\sqrt{2}~\cdots\cdots①
\end{align*}
$\theta=\dfrac{\pi}{2}+2n\pi$($n$ は整数)のとき,(*)は成り立たないから,$\theta\neq\dfrac{\pi}{2}+2n\pi$ である。すなわち $\cos\theta\neq0$ であるから,①の両辺を $\cos^2\theta>0$ で割って
\begin{align*}
&3\left(\dfrac{2\sin\theta}{\cos\theta}+1-\dfrac{\sin^2\theta}{\cos^2\theta}\right)\geqq\dfrac{\sqrt{2}}{\cos^2\theta} \\[4pt]
&3(2\tan\theta+1-\tan^2\theta)\geqq\sqrt{2}(1+\tan^2\theta) \\[4pt]
&(3+\sqrt{2})\tan^2\theta-6\tan\theta-(3-\sqrt{2})\leqq0 \\[4pt]
&\{\tan\theta-(3-\sqrt{2})\}\{(3+\sqrt{2})\tan\theta+1\}\leqq0 \\[4pt]
&-\dfrac{1}{3+\sqrt{2}}\leqq\tan\theta\leqq3-\sqrt{2} \\[4pt]
&\dfrac{\sqrt{2}-3}{7}\leqq\tan\theta\leqq3-\sqrt{2}
\end{align*}
よって,最小値は $\dfrac{\sqrt{2}-3}{7}$,最大値は $3-\sqrt{2}$ である。&3\left(\dfrac{2\sin\theta}{\cos\theta}+1-\dfrac{\sin^2\theta}{\cos^2\theta}\right)\geqq\dfrac{\sqrt{2}}{\cos^2\theta} \\[4pt]
&3(2\tan\theta+1-\tan^2\theta)\geqq\sqrt{2}(1+\tan^2\theta) \\[4pt]
&(3+\sqrt{2})\tan^2\theta-6\tan\theta-(3-\sqrt{2})\leqq0 \\[4pt]
&\{\tan\theta-(3-\sqrt{2})\}\{(3+\sqrt{2})\tan\theta+1\}\leqq0 \\[4pt]
&-\dfrac{1}{3+\sqrt{2}}\leqq\tan\theta\leqq3-\sqrt{2} \\[4pt]
&\dfrac{\sqrt{2}-3}{7}\leqq\tan\theta\leqq3-\sqrt{2}
\end{align*}