Contents
点と直線の距離を求める

ヒロ
平面上の点と直線の距離を求めよう。
【点と直線の距離】
点P$(p,~q)$ と直線 $ax+by+c=0~\cdots\cdots①$ の距離を $d$ とする。
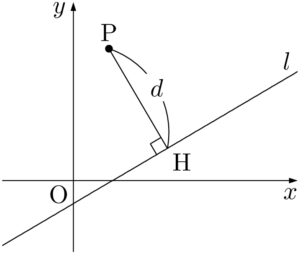
点Hの座標を求めれば,2点P,Hの座標からPHの長さを求めることができる。ここで,点Pを通り $l$ に垂直な直線を $m$ とすると,2直線 $l,~m$ の交点が点Hである。直線 $m$ の方程式は
\begin{align*}
&b(x-p)-a(y-q)=0 \\[4pt]
&bx-ay-bp+aq=0~\cdots\cdots②
\end{align*}
$①\times a+②\times b$ より&b(x-p)-a(y-q)=0 \\[4pt]
&bx-ay-bp+aq=0~\cdots\cdots②
\end{align*}
\begin{align*}
(a^2+b^2)x+ca-b^2p+abq=0
\end{align*}
$a$ と $b$ が同時に0になることはないから,$a^2+b^2\neq0$(a^2+b^2)x+ca-b^2p+abq=0
\end{align*}
よって,$x=\dfrac{b^2p-abq-ca}{a^2+b^2}$
$①\times b-②\times a$ より
\begin{align*}
&(b^2+a^2)y+bc+abp-a^2q=0 \\[4pt]
&y=\dfrac{-abp+a^2q-bc}{a^2+b^2}
\end{align*}
したがって,H$\left(\dfrac{b^2p-abq-ca}{a^2+b^2},~\dfrac{-abp+a^2q-bc}{a^2+b^2}\right)$&(b^2+a^2)y+bc+abp-a^2q=0 \\[4pt]
&y=\dfrac{-abp+a^2q-bc}{a^2+b^2}
\end{align*}
このとき,PHの長さの2乗は
\begin{align*}
\text{PH}^2&=\left(p-\dfrac{b^2p-abq-ca}{a^2+b^2}\right)^2+\left(q-\dfrac{-abp+a^2q-bc}{a^2+b^2}\right)^2 \\[4pt]
&=\left(\dfrac{a^2p+abq+ca}{a^2+b^2}\right)^2+\left(\dfrac{abp+b^2q+bc}{a^2+b^2}\right)^2 \\[4pt]
&=(ap+bq+c)^2\left(\dfrac{a^2}{(a^2+b^2)^2}+\dfrac{b^2}{(a^2+b^2)^2}\right)^2 \\[4pt]
&=\dfrac{(ap+bq+c)^2}{a^2+b^2}
\end{align*}
$\text{PH}\geqq0$ であるから\text{PH}^2&=\left(p-\dfrac{b^2p-abq-ca}{a^2+b^2}\right)^2+\left(q-\dfrac{-abp+a^2q-bc}{a^2+b^2}\right)^2 \\[4pt]
&=\left(\dfrac{a^2p+abq+ca}{a^2+b^2}\right)^2+\left(\dfrac{abp+b^2q+bc}{a^2+b^2}\right)^2 \\[4pt]
&=(ap+bq+c)^2\left(\dfrac{a^2}{(a^2+b^2)^2}+\dfrac{b^2}{(a^2+b^2)^2}\right)^2 \\[4pt]
&=\dfrac{(ap+bq+c)^2}{a^2+b^2}
\end{align*}
\begin{align*}
\text{PH}=\dfrac{\abs{ap+bq+c}}{\sqrt{a^2+b^2}}
\end{align*}
\text{PH}=\dfrac{\abs{ap+bq+c}}{\sqrt{a^2+b^2}}
\end{align*}

ヒロ
上では点Hの座標を求めてからPHの長さを求めたが,点Hの座標を求めずにPHの長さを求めることもできる。
【うまく計算する】
$l$ の方程式 $ax+by+c=0$ より
\begin{align*}
a(x-p)+b(y-q)=-ap-bq-c~\cdots\cdots①
\end{align*}
点P$(p,~q)$ を通り,$l$ に垂直な直線 $m$ の方程式はa(x-p)+b(y-q)=-ap-bq-c~\cdots\cdots①
\end{align*}
\begin{align*}
b(x-p)-a(y-q)=0~\cdots\cdots②
\end{align*}
$①^2+②^2$ よりb(x-p)-a(y-q)=0~\cdots\cdots②
\end{align*}
\begin{align*}
&(a^2+b^2)\{(x-p)^2+(y-q)^2\}=(-ap-bq-c)^2 \\[4pt]
&(x-p)^2+(y-q)^2=\dfrac{(ap+bq+c)^2}{a^2+b^2}
\end{align*}
よって&(a^2+b^2)\{(x-p)^2+(y-q)^2\}=(-ap-bq-c)^2 \\[4pt]
&(x-p)^2+(y-q)^2=\dfrac{(ap+bq+c)^2}{a^2+b^2}
\end{align*}
\begin{align*}
\text{PH}&=\sqrt{(x-p)^2+(y-q)^2} \\[4pt]
&=\dfrac{\abs{ap+bq+c}}{\sqrt{a^2+b^2}}
\end{align*}
\text{PH}&=\sqrt{(x-p)^2+(y-q)^2} \\[4pt]
&=\dfrac{\abs{ap+bq+c}}{\sqrt{a^2+b^2}}
\end{align*}

ヒロ
次の記事で説明しているように,ベクトルの内積の図形的意味を利用すると,比較的楽に点と直線の距離の公式を導出することができる。
点と直線の距離の公式

ヒロ
点と直線の距離の公式は次のようになっている。
点と直線の距離の公式点P$(p,~q)$ と直線 $ax+by+c=0$ との距離を $d$ とすると
\begin{align*}
d=\dfrac{\abs{ap+bq+c}}{\sqrt{a^2+b^2}}
\end{align*}
d=\dfrac{\abs{ap+bq+c}}{\sqrt{a^2+b^2}}
\end{align*}

ヒロ
公式を間違える人のほとんどが,分母を $\sqrt{p^2+q^2}$ としてしまうので注意しよう。

ヒロ
公式を導出する際の計算を思い出すと,分母を間違えることがなくなると思う。
点と直線の距離に関する問題【福岡大】
2012年 福岡大曲線 $y=x^2-1$ 上を動く点Pと,直線 $y=x-3$ 上を動く点Qとの距離が最小となるときの点Qの座標は $\myhako$ であり,このときの距離は $\myhako$ である。
【考え方と解答】
2点間の距離を考えるとき,その2つの点が両方とも動く場合は,まず片方の点を固定して考えるようにしよう。片方の点を固定したときにもう1つの点がどのような位置にあるかを考える。次に,固定していた点を動かしていくのがセオリーである。
この問題では2点P,Qのうち,どちらを固定して考えるかがポイントとなる。点Qを固定すると,直線上のある点Qから放物線 $y=x^2-1$ 上の点までの距離が最小となる点を考えることになる。点Pを固定すると,点Pと直線 $y=x-3$ との距離を考えることになる。
点と直線の距離の公式を知ったばかりであれば,点Pを固定して考えた方が,考えやすいかもしれないので,今回はこちらで考えることにする。
点Pを固定したとき,PQの長さが最小になる点Qは,点Pから直線 $y-x-3$ に下ろした垂線の足Hと一致する。
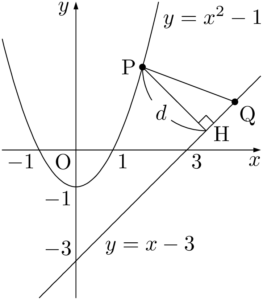
次に点Pを動かすと,直線 $y=x-3$ に垂直な線分PHが動く。その中でPHの長さが最小になるような点Pを探そう。
点Pは放物線 $y=x^2-1$ 上の点であるから,実数 $t$ を用いてP$(t,~t^2-1)$ と表せる。点Pと直線 $x-y-3=0$ との距離を $d$ とすると
①,②より $y$ を消去すると
よって,点Qの座標はQ$\left(\dfrac{11}{8},~-\dfrac{13}{8}\right)$ であり,PQの距離は $\dfrac{7\sqrt{2}}{8}$ である。
2点間の距離を考えるとき,その2つの点が両方とも動く場合は,まず片方の点を固定して考えるようにしよう。片方の点を固定したときにもう1つの点がどのような位置にあるかを考える。次に,固定していた点を動かしていくのがセオリーである。
この問題では2点P,Qのうち,どちらを固定して考えるかがポイントとなる。点Qを固定すると,直線上のある点Qから放物線 $y=x^2-1$ 上の点までの距離が最小となる点を考えることになる。点Pを固定すると,点Pと直線 $y=x-3$ との距離を考えることになる。
点と直線の距離の公式を知ったばかりであれば,点Pを固定して考えた方が,考えやすいかもしれないので,今回はこちらで考えることにする。
点Pを固定したとき,PQの長さが最小になる点Qは,点Pから直線 $y-x-3$ に下ろした垂線の足Hと一致する。

次に点Pを動かすと,直線 $y=x-3$ に垂直な線分PHが動く。その中でPHの長さが最小になるような点Pを探そう。
点Pは放物線 $y=x^2-1$ 上の点であるから,実数 $t$ を用いてP$(t,~t^2-1)$ と表せる。点Pと直線 $x-y-3=0$ との距離を $d$ とすると
\begin{align*}
d&=\dfrac{\abs{t-(t^2-1)-3}}{\sqrt{1^2+1^2}} \\[4pt]
&=\dfrac{\abs{t^2-t+2}}{\sqrt{2}}
\end{align*}
ここでd&=\dfrac{\abs{t-(t^2-1)-3}}{\sqrt{1^2+1^2}} \\[4pt]
&=\dfrac{\abs{t^2-t+2}}{\sqrt{2}}
\end{align*}
\begin{align*}
t^2-t+2=\left(t-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0
\end{align*}
であるからt^2-t+2=\left(t-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0
\end{align*}
\begin{align*}
d=\dfrac{1}{\sqrt{2}}\left(t-\dfrac{1}{2}\right)^2+\dfrac{7}{4\sqrt{2}}
\end{align*}
$t$ はすべての実数をとり得るから,$t=\dfrac{1}{2}$ のとき,$d$ は最小となり,最小値はd=\dfrac{1}{\sqrt{2}}\left(t-\dfrac{1}{2}\right)^2+\dfrac{7}{4\sqrt{2}}
\end{align*}
\begin{align*}
\dfrac{7}{4\sqrt{2}}=\dfrac{7\sqrt{2}}{8}
\end{align*}
このとき,P$\left(\dfrac{1}{2},~-\dfrac{3}{4}\right)$ であるから,点Pを通り,直線 $x-y-3=0$ に垂直な直線の方程式は\dfrac{7}{4\sqrt{2}}=\dfrac{7\sqrt{2}}{8}
\end{align*}
\begin{align*}
&\left(x-\dfrac{1}{2}\right)+\left(y+\dfrac{3}{4}\right)=0 \\[4pt]
&y=-x-\dfrac{1}{4}
\end{align*}
点Qは2直線 $y=x-3~\cdots\cdots①$,$y=-x-\dfrac{1}{4}~\cdots\cdots②$ の交点である。&\left(x-\dfrac{1}{2}\right)+\left(y+\dfrac{3}{4}\right)=0 \\[4pt]
&y=-x-\dfrac{1}{4}
\end{align*}
①,②より $y$ を消去すると
\begin{align*}
&x-3=-x-\dfrac{1}{4} \\[4pt]
&x=\dfrac{11}{8}
\end{align*}
①より,$y=-\dfrac{13}{8}$&x-3=-x-\dfrac{1}{4} \\[4pt]
&x=\dfrac{11}{8}
\end{align*}
よって,点Qの座標はQ$\left(\dfrac{11}{8},~-\dfrac{13}{8}\right)$ であり,PQの距離は $\dfrac{7\sqrt{2}}{8}$ である。

ヒロ
詳しく説明することはしないが,点Pの位置について軽く触れておく。
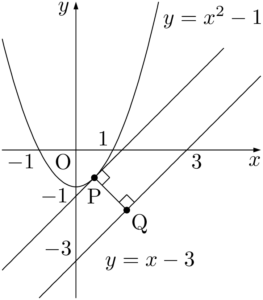
【直線を平行移動して接する点を探せ】
放物線上の点Pと直線上の点Qに対して,PQの長さが最小になるような点Pは,直線 $y=x-3$ を平行移動して放物線 $y=x^2-1$ と接するときの接点になっている。

ヒロ
今回のように空欄を埋めるだけの問題であれば,このことを利用すれば,もう少し楽に点Pの座標を求めることができる。

ヒロ
ここではその解答を書かないが,微分の記事で同じ問題を扱うのも良いかもしれない。