ここでは平面ベクトルについて解説します。
まず,ベクトルとは何かを知りましょう。ベクトルを一言で表すと「矢印」です。
「矢印」の扱い方は「伸ばす」と「つなぐ」です。演算のルールを覚えてベクトルを扱えるようにしましょう。
演算ルールを覚えるだけで解ける大学入試問題もあります。
有向線分とベクトル

ヒロ
まずは有向線分とベクトルについて知ろう。
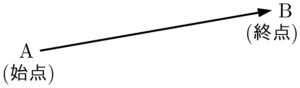
有向線分とベクトル 線分ABにおいて,点Aから点Bへの向きを指定したとき,これを有向線分ABという。有向線分においてAを始点,Bを終点という。また,線分ABの長さを有向線分ABの大きさまたは長さという。
有向線分の位置の違いを無視して,その向きと大きさのみに着目したものをベクトルという。有向線分ABが表すベクトルを $\Vec{AB}$ と書き,その大きさを $\abs{\Vec{AB}}$ と書く。
ベクトルは,1つの文字と矢印を用いて $\vec{a}$ と表すこともある。$\vec{a}$ の大きさは $\abs{\vec{a}}$ と書く。
有向線分の位置の違いを無視して,その向きと大きさのみに着目したものをベクトルという。有向線分ABが表すベクトルを $\Vec{AB}$ と書き,その大きさを $\abs{\Vec{AB}}$ と書く。
ベクトルは,1つの文字と矢印を用いて $\vec{a}$ と表すこともある。$\vec{a}$ の大きさは $\abs{\vec{a}}$ と書く。

ベクトルの相等
ベクトルの相等 2つのベクトルについて「$\vec{a}$ と $\vec{b}$ が等しい」のは,$\vec{a}$ と $\vec{b}$ の向きが同じで大きさも等しいことであり,これを $\vec{a}=\vec{b}$ と表す。

ヒロ
ベクトルは有向線分と異なり,位置を無視するため,始点が異なっていても,向きが同じで大きさが等しければ等しいベクトルであると言えることに注意しよう。
零ベクトル・単位ベクトル・逆ベクトル

ヒロ
大きさが0のベクトルを零ベクトルといい,$\vec{0}$ と表す。また,大きさが1のベクトルを単位ベクトルという。

ヒロ
ベクトル $\vec{a}$ と大きさが等しく,向きが反対のベクトルを $\vec{a}$ の逆ベクトルといい,$-\vec{a}$ と表す。
ベクトルの演算

ヒロ
ベクトルの演算ルールを知って覚えよう。

ヒロ
まずは,ベクトルの加法について知ろう。
ベクトルの加法始点を揃える場合は,四角形OACBが平行四辺形となるような点Cをとると,$\Vec{OC}=\vec{a}+\vec{b}$ となる。
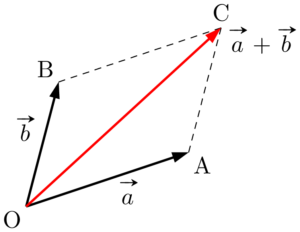
$\vec{b}$ の始点が $\vec{a}$ の終点と重なるように平行移動することで,2つのベクトルの始点と終点を結ぶことで $\Vec{OC}=\vec{a}+\vec{b}$ が得られる。
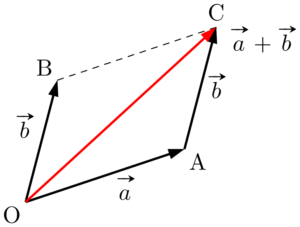

$\vec{b}$ の始点が $\vec{a}$ の終点と重なるように平行移動することで,2つのベクトルの始点と終点を結ぶことで $\Vec{OC}=\vec{a}+\vec{b}$ が得られる。


ヒロ
次はベクトルの減法について知ろう。
ベクトルの減法逆ベクトルを利用して,$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$ と考えることで,ベクトルの減法を加法として捉えることができる。



ヒロ
$\Vec{OA}-\Vec{OB}=\Vec{BA}$ となるが,これは右辺から左辺への変形を始点を変える公式として使えるようにすると良いだろう。

ヒロ
次はベクトルの実数倍について知ろう。
ベクトルの実数倍$k$ を実数として,$k\vec{a}$ を考えるとき,向きは $k>0$ のとき $\vec{a}$ と同じ向きで,$k<0$ のとき $\vec{a}$ と反対向きである。$k=0$ のとき $\vec{0}$ となる。
2019年 東京理科大
2019年 東京理科大平面上,$\textrm{OA}/\!/\textrm{CB}$,$\textrm{OC}/\!/\textrm{AB}$ である平行四辺形OABCを考える。辺ABを $2:3$ に内分する点をD,辺CBを $1:4$ に外分する点をEとする。
(1) $\Vec{DE}=-\dfrac{\myhako}{\myhako}\Vec{OA}+\dfrac{\myhako}{\myhako}\Vec{OC}$ である。
(2) 線分DEと線分OBの交点をFとすると,
(1) $\Vec{DE}=-\dfrac{\myhako}{\myhako}\Vec{OA}+\dfrac{\myhako}{\myhako}\Vec{OC}$ である。
(2) 線分DEと線分OBの交点をFとすると,
\begin{align*}
\Vec{OF}=\dfrac{\myhako}{\myhako}\Vec{OA}+\dfrac{\myhako}{\myhako}\Vec{OC}
\end{align*}
である。\Vec{OF}=\dfrac{\myhako}{\myhako}\Vec{OA}+\dfrac{\myhako}{\myhako}\Vec{OC}
\end{align*}
【(1)の解答と考え方】
まずは図を描いて状況を把握しよう。
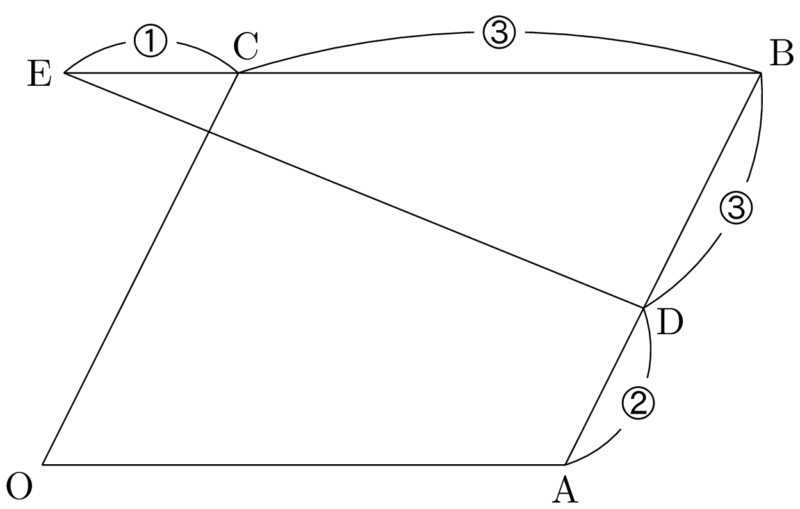
$\Vec{DE}$ を $\Vec{OA}$ と $\Vec{OC}$ で表すことを考えるから,始点を変える必要がある。DはABを $2:3$ に内分する点であるから
まずは図を描いて状況を把握しよう。

$\Vec{DE}$ を $\Vec{OA}$ と $\Vec{OC}$ で表すことを考えるから,始点を変える必要がある。DはABを $2:3$ に内分する点であるから
\begin{align*}
\Vec{OD}&=\Vec{OA}+\dfrac{2}{5}\Vec{AB} \\[4pt]
&=\Vec{OA}+\dfrac{2}{5}\Vec{OC}
\end{align*}
また,EはCBを $1:4$ に外分する点であるから\Vec{OD}&=\Vec{OA}+\dfrac{2}{5}\Vec{AB} \\[4pt]
&=\Vec{OA}+\dfrac{2}{5}\Vec{OC}
\end{align*}
\begin{align*}
\Vec{OE}&=\Vec{OC}+\dfrac{1}{3}\Vec{BC} \\[4pt]
&=\Vec{OC}-\dfrac{1}{3}\Vec{OA}
\end{align*}
よって\Vec{OE}&=\Vec{OC}+\dfrac{1}{3}\Vec{BC} \\[4pt]
&=\Vec{OC}-\dfrac{1}{3}\Vec{OA}
\end{align*}
\begin{align*}
\Vec{DE}&=\Vec{OE}-\Vec{OD} \\[4pt]
&=\Vec{OC}-\dfrac{1}{3}\Vec{OA}-\left(\Vec{OA}+\dfrac{2}{5}\Vec{OC}\right) \\[4pt]
&=-\dfrac{4}{3}\Vec{OA}+\dfrac{3}{5}\Vec{OC}
\end{align*}
\Vec{DE}&=\Vec{OE}-\Vec{OD} \\[4pt]
&=\Vec{OC}-\dfrac{1}{3}\Vec{OA}-\left(\Vec{OA}+\dfrac{2}{5}\Vec{OC}\right) \\[4pt]
&=-\dfrac{4}{3}\Vec{OA}+\dfrac{3}{5}\Vec{OC}
\end{align*}
(2) 線分DEと線分OBの交点をFとすると,
\begin{align*}である。
\Vec{OF}=\dfrac{\myhako}{\myhako}\Vec{OA}+\dfrac{\myhako}{\myhako}\Vec{OC}
\end{align*}
【(2)の解答と考え方】
DEとOAの交点をGとする。
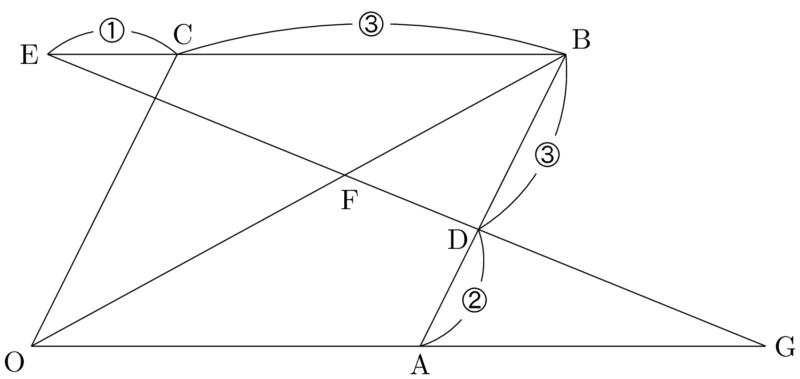
$\sankaku{DAG}$ と $\sankaku{DBE}$ は相似であり,相似比は $\textrm{AD}:\textrm{DB}=2:3$ であるから $\textrm{AG}:\textrm{BE}=2:3$ である。よって
DEとOAの交点をGとする。

$\sankaku{DAG}$ と $\sankaku{DBE}$ は相似であり,相似比は $\textrm{AD}:\textrm{DB}=2:3$ であるから $\textrm{AG}:\textrm{BE}=2:3$ である。よって
\begin{align*}
\textrm{OA}&=\textrm{BC} \\[4pt]
&=\dfrac{3}{2}\textrm{AG}\times\dfrac{3}{4} \\[4pt]
&=\dfrac{9}{8}\textrm{AG}
\end{align*}
となるから\textrm{OA}&=\textrm{BC} \\[4pt]
&=\dfrac{3}{2}\textrm{AG}\times\dfrac{3}{4} \\[4pt]
&=\dfrac{9}{8}\textrm{AG}
\end{align*}
\begin{align*}
\textrm{OG}:\textrm{BE}&=(\textrm{OA}+\textrm{AG}):\dfrac{3}{2}\textrm{AG} \\[4pt]
&=\dfrac{17}{8}\textrm{AG}:\dfrac{3}{2}\textrm{AG} \\[4pt]
&=17:12
\end{align*}
$\sankaku{OFG}$ と $\sankaku{BFE}$ は相似であるから\textrm{OG}:\textrm{BE}&=(\textrm{OA}+\textrm{AG}):\dfrac{3}{2}\textrm{AG} \\[4pt]
&=\dfrac{17}{8}\textrm{AG}:\dfrac{3}{2}\textrm{AG} \\[4pt]
&=17:12
\end{align*}
\begin{align*}
\textrm{OF}:\textrm{FB}=17:12
\end{align*}
したがって\textrm{OF}:\textrm{FB}=17:12
\end{align*}
\begin{align*}
\Vec{OF}&=\dfrac{17}{29}\Vec{OB} \\[4pt]
&=\dfrac{17}{29}\Vec{OA}+\dfrac{17}{29}\Vec{OC}
\end{align*}
\Vec{OF}&=\dfrac{17}{29}\Vec{OB} \\[4pt]
&=\dfrac{17}{29}\Vec{OA}+\dfrac{17}{29}\Vec{OC}
\end{align*}