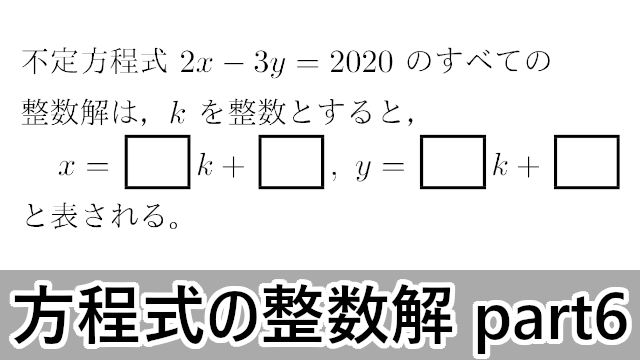
ここでは不定方程式の整数解に関する問題について説明します。
不定方程式の右辺が1以外の数になると,整数解の1つを見つけることが難しくなることがあります。
そんな場合に役に立つ「整数解の見つけ方」を知っておくことが重要です。
様々な手法・解法を知り,身に付けることで,大学入試問題に対応できるようにしましょう。
Contents
不定方程式の問題【芝浦工大】

ヒロ
まずは不定方程式の右辺が1以外だけど,比較的整数解を見つけやすい問題を解いてみよう。
2018年 芝浦工大方程式 $3x-4y=2$ の整数解をすべて求めよ。
【考え方と解答】
3の倍数と4の倍数の差が2になるときを考えて「$6-4=2$」を思い浮かべることができれば,1つの整数解として $x=2,~y=1$ を見つけることができる。
よって,与えられた方程式より
3の倍数と4の倍数の差が2になるときを考えて「$6-4=2$」を思い浮かべることができれば,1つの整数解として $x=2,~y=1$ を見つけることができる。
よって,与えられた方程式より
\begin{align*}
3(x-2)-4(y-1)=0
\end{align*}
となる。3と4は互いに素であるから,整数 $n$ を用いて3(x-2)-4(y-1)=0
\end{align*}
\begin{align*}
&\begin{cases}
x-2=4n \\[4pt]
y-1=3n
\end{cases} \\[4pt]
&\begin{cases}
x=4n+2 \\[4pt]
y=3n+1
\end{cases}
\end{align*}
&\begin{cases}
x-2=4n \\[4pt]
y-1=3n
\end{cases} \\[4pt]
&\begin{cases}
x=4n+2 \\[4pt]
y=3n+1
\end{cases}
\end{align*}