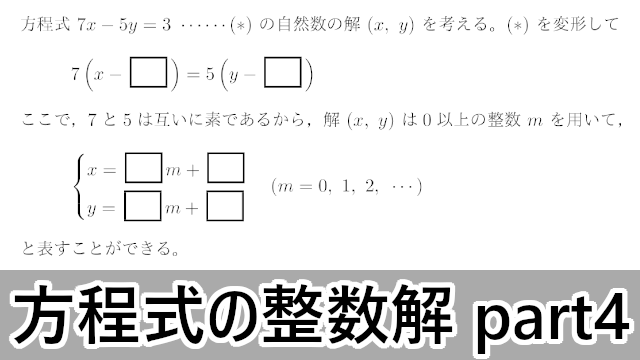
方程式の整数解に関する様々な問題が,大学入試で出題されますが,今回はその中でも特に出題頻度が高いものを扱います。
様々な問題を解くことで,解法を知って,解ける問題を増やしていきましょう。
Contents
- ページ1
- 1 不定方程式の基本問題
- ページ2
- 1 不定方程式の問題【昭和女子大】
- ページ3
- 1 不定方程式の問題2【立命館大】
不定方程式の基本問題

ヒロ
まずは簡単な問題から不定方程式の基本的解法をマスターしよう。
問題方程式 $2x-3y=0$ の整数解をすべて求めよ。
プリントを次のリンクからダウンロードできます。
【考え方と解答】
与えられた方程式より
例えば,3と互いに素でない6が $x$ の係数の場合は,$x$ が整数のとき $6x$ は常に3の倍数であるから,$x$ が3の倍数ということにはならない。
つまり3と互いに素でない数が $x$ の係数になっていると,「$x$ が3の倍数である」といえなくなることに注意しよう。
$x$ が3の倍数であるから,整数 $k$ を用いて $x=3k$ と表すことができるから
与えられた方程式より
\begin{align*}
2x=3y
\end{align*}
右辺は3の倍数であるから,左辺の $2x$ も3の倍数である。つまり,$x$ が3の倍数である。ここで注意することは $x$ の係数が3と互いに素な2になっていること。2x=3y
\end{align*}
例えば,3と互いに素でない6が $x$ の係数の場合は,$x$ が整数のとき $6x$ は常に3の倍数であるから,$x$ が3の倍数ということにはならない。
つまり3と互いに素でない数が $x$ の係数になっていると,「$x$ が3の倍数である」といえなくなることに注意しよう。
$x$ が3の倍数であるから,整数 $k$ を用いて $x=3k$ と表すことができるから
\begin{align*}
&2\Cdota3k=3y \\[4pt]
&y=2k
\end{align*}
よって,求める整数解は&2\Cdota3k=3y \\[4pt]
&y=2k
\end{align*}
\begin{align*}
x=3k,~y=2k~(k~は整数)
\end{align*}
x=3k,~y=2k~(k~は整数)
\end{align*}
不定方程式の基本2つの整数 $a,~b$ が互いに素であるとき,方程式
\begin{align*}
ax-by=0
\end{align*}
の整数解はax-by=0
\end{align*}
\begin{align*}
x=bk,~y=ak~(k~は整数)
\end{align*}
と表すことができる。x=bk,~y=ak~(k~は整数)
\end{align*}