図形の性質の考え方・解き方の第二弾です。第一弾をご覧になっていない方は,お手数ですが,まずは第一弾をご覧ください。理解がしやすくなるはずです。
センター試験の数学IAの図形問題の考え方を説明します。
\mathrm{AB=2,~BC=3,~CD=1},~\kaku{ABC}=60\Deg
\end{align*}
&\kaku{CDA}=\myBox{アイウ}\Deg \\[4pt]
&\mathrm{AC}=\sqrt{\myBox{エ}} \\[4pt]
&\mathrm{AD}=\myBox{オ}
\end{align*}
\sin\kaku{BAC}=\dfrac{\myBox{カ}\sqrt{\myBox{キク}}}{14}
\end{align*}
\mathrm{BD}=\dfrac{\myBox{ケ}\sqrt{\myBox{コ}}}{\myBox{サ}}
\end{align*}
Contents
60°をできるだけ正確に描く方法

外接円が関係しているから,まずは円から描こう。$B=60\Deg$ だから,前回伝えた「1つの角が $60\Deg$ のときの図の描き方」を利用して図を描こう。

円を描いてから,辺ACを描く。

次に $\mathrm{AB=2,~BC=3}$ となるように点Bを優弧AC上にとる。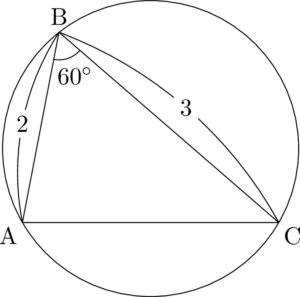

「四角形ABCD」となっているから,$\mathrm{A\to B\to C\to D\to A}$ と結んだときに四角形になる。よって,点Dは劣弧AC上にあることが分かる。$\mathrm{CD=1}$ だから,CDの長さがABの半分の長さになるような位置に点Dをとる。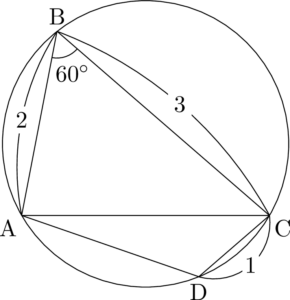

問題文を読んで図を描いたときに,ここまで描くことができる。
1999年センターIA(図形)の一般的な考え方と解法

それでは $\kaku{CDA}$ から順に求めていこう。

最初は簡単ですね。四角形ABCDが円に内接するから,$\kaku{CDA}=120\Deg$ です。

そうだね。円に内接する四角形の対角の和が $180\Deg$ になることを知っていればすぐに求められる。

次はACを求めよう。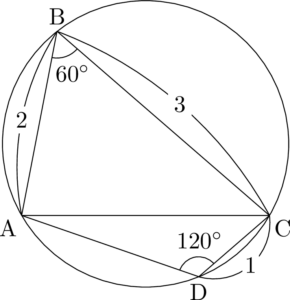

ACを求めるんだから,2辺とその間の角が分かっている $\sankaku{ABC}$ に着目して,余弦定理ですね。
\mathrm{AC}^2&=2^2+3^2-2\Cdota2\Cdota3\cos60\Deg \\[4pt]
&=4+9-6=7
\end{align*}

次はADを求めよう。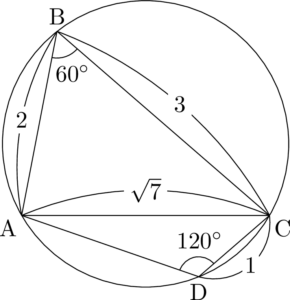

まず,ADを含む $\sankaku{ACD}$ に着目します。1組の角と対辺が分かっているけど,$\kaku{ACD}$ が分からないので,正弦定理は使えません。ということで,やっぱり余弦定理ですね。
&(\sqrt{7})^2=1^2+{\mathrm{AD}}^2-2\Cdota1\Cdota\mathrm{AD}\cos120\Deg \\[4pt]
&{\mathrm{AD}}^2+\mathrm{AD}-6=0 \\[4pt]
&(\mathrm{AD}+3)(\mathrm{AD}-2)=0 \\[4pt]
&\mathrm{AD}=-3,~2
\end{align*}

次は $\sin\kaku{BAC}$ を求めよう。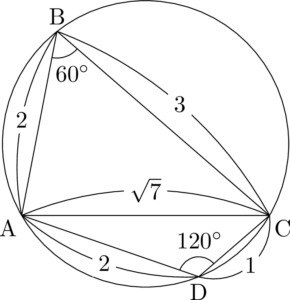

$\sin$ の値を求めるので,$\sankaku{ABC}$ に着目して正弦定理ですね。
&\dfrac{\sqrt{7}}{\sin60\Deg}=\dfrac{3}{\sin\kaku{BAC}} \\[4pt]
&\sqrt{7}\sin\kaku{BAC}=3\sin60\Deg \\[4pt]
&\sin\kaku{BAC}=\dfrac{3}{\sqrt{7}}\Cdota\dfrac{\sqrt{3}}{2} \\[4pt]
&\sin\kaku{BAC}=\dfrac{3\sqrt{21}}{14}
\end{align*}

それでは最後のBDを求めよう。

これは前回教えてもらったトレミーの定理で簡単に求められます。
&2\Cdota1+2\Cdota3=\sqrt{7}\mathrm{BD} \\[4pt]
&\mathrm{BD}=\dfrac{8}{\sqrt{7}} \\[4pt]
&\mathrm{BD}=\dfrac{8\sqrt{7}}{7}
\end{align*}
1999年センターIA(図形) の裏技解法【図を描いた時点で求まっている】

実は最初に描いた図の時点で,$\kaku{ADC}=120\Deg$ がすぐ分かるのは当然として,もう少し分かる部分がある。

下図で赤字の部分は,知っている三角形を増やせば,すぐに図に書き込むことができる。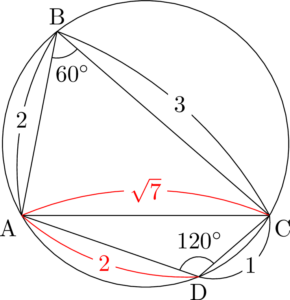

実はこの問題で使われている三角形も有名な三角形なので覚えよう。
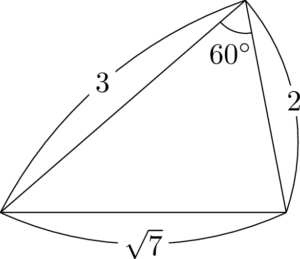
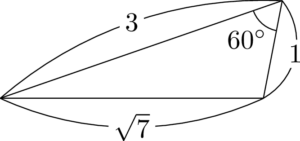
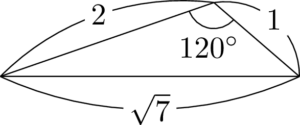

$1,~2,~3$ は一郎,次郎,三郎の三兄弟で,$\sqrt{7}$ はルナちゃん。

しょうもなさすぎて覚えられるかも。

覚えられるならどんな覚え方でもいいよ。$\sqrt{7}$ の対角が $60\Deg$ か $120\Deg$ になってるよ。

辺の長さから $120\Deg$ になるのは1と2のときと分かるかもしれないけど,「1と2だから ${\color{red}1}{\color{blue}2}0\Deg$ だ」と覚えておけば良いだろう。

3つの三角形を組み合わせると次のようになる。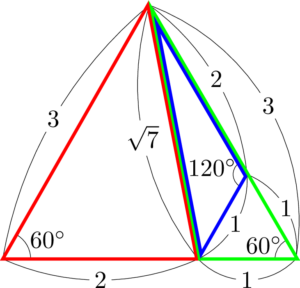

ということで,知っているから $\mathrm{AC}=\sqrt{7}$ も $\mathrm{AD}=2$ も分かってしまう。

前の「名古屋で悩み,七五三」も正三角形にできましたけど,他にもあるんですか?

いくらでも作れるんだけど,試験で扱いやすいのが,3辺とも整数ということを考えると,もう1つくらいかな。それもここで言っておこうか。

はい。お願いします!
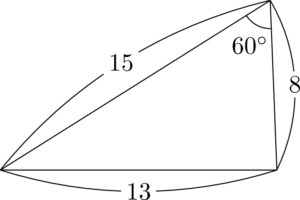
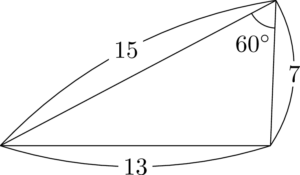
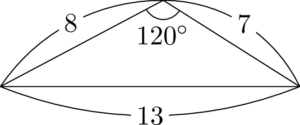

13が父さん,15と8で行こうや,15と7で行こな,7と8で那覇。13の対角が $60\Deg$ か $120\Deg$ になってるのに注意。

3つの三角形を組み合わせると次のようになる。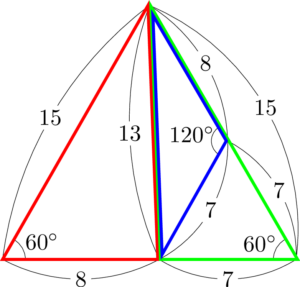
正弦定理は垂線の長さに関する等式だった

次は正弦定理の捉え方を少し変えてもらおう。

公式通りに立式すると,さっき解いてもらったように分数になるから鬱陶しく感じるんだよね。

そうですね・・・

そこで初めから $\sin$ が分母に来ないように立式できるようになろう。
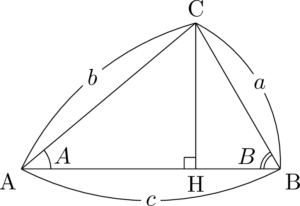
$\sankaku{ACH}$ に着目すると
\mathrm{CH}=b\sin A
\end{align*}
\mathrm{CH}=a\sin B
\end{align*}

正弦定理って三角形を垂線で二つに分けて,垂線の長さに関する等式だったんですね。

$\sin\kaku{BAC}$ を求めたときに正弦定理を使ったけど,垂線の長さに着目する考え方で立式すると1行省略できるため速くなる。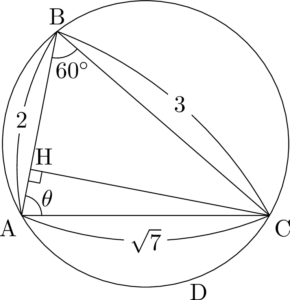
&\sqrt{7}\sin\theta=3\sin60\Deg \\[4pt]
&\sin\theta=\dfrac{3\sqrt{3}}{2\sqrt{7}}=\dfrac{3\sqrt{21}}{14}
\end{align*}

あと $\sin$ の値を求めるのに面積を利用する解法も覚えておこう。
&\dfrac{1}{2}\Cdota2\Cdota\sqrt{7}\sin\theta=\dfrac{1}{2}\Cdota2\Cdota3\sin60\Deg \\[4pt]
&\sin\theta=\dfrac{3\sqrt{21}}{14}
\end{align*}

そのときの状況に応じて,色々な考え方ができるようにしよう。

頑張ります!
まとめ

知っている三角形が多ければ,計算することなく,見た瞬間に答えが出る場合もある。また,正弦定理で立てる最初の式が分数になるのが嫌な人は「垂線の長さが等しい」ことを考えて分数にならないように立式するのもアリ。





















