Contents
複素数の加法・減法【静岡理工科大】
2004年 静岡理工科大$1+i+i^2+i^3+i^4+i^5+\cdots+i^{99}+i^{100}+i^{101}$ を計算すると $\myhako$ となる。ただし,$i$ は虚数単位である。
【考え方と解答】
$i^2=-1$ になることに注意して計算しよう。
$i^2=-1$ になることに注意して計算しよう。
\begin{align*}
1+i+i^2+i^3=1+i+(-1)+(-i)=0
\end{align*}
であるから1+i+i^2+i^3=1+i+(-1)+(-i)=0
\end{align*}
\begin{align*}
(与式)&=(1+i+i^2+i^3)(1+i^4+i^8+\cdots+i^{96})+i^{100}+i^{101} \\[4pt]
&=i^{100}(1+i) \\[4pt]
&=(i^2)^{50}(1+i) \\[4pt]
&=(-1)^{50}(1+i) \\[4pt]
&=1+i
\end{align*}
(与式)&=(1+i+i^2+i^3)(1+i^4+i^8+\cdots+i^{96})+i^{100}+i^{101} \\[4pt]
&=i^{100}(1+i) \\[4pt]
&=(i^2)^{50}(1+i) \\[4pt]
&=(-1)^{50}(1+i) \\[4pt]
&=1+i
\end{align*}
複素数の乗法【東京都市大】
2009年 東京都市大$(\sqrt{3}+\sqrt{2}i)(-\sqrt{5}+2\sqrt{3}i)$ を計算せよ。ただし,$i$ は虚数単位とする。
【考え方と解答】
\begin{align*}
(与式)&=-\sqrt{15}+6i-\sqrt{10}i+2\sqrt{6}i^2 \\[4pt]
&=(-\sqrt{15}-2\sqrt{6})+(6-\sqrt{10})i
\end{align*}
(与式)&=-\sqrt{15}+6i-\sqrt{10}i+2\sqrt{6}i^2 \\[4pt]
&=(-\sqrt{15}-2\sqrt{6})+(6-\sqrt{10})i
\end{align*}
2020年 北里大$(\sqrt{5}-i)^3=\myhako\sqrt{\myhako}+\myhako\,i$ である。ただし $i$ は虚数単位である。
【考え方と解答】
3乗の展開公式を利用しよう。
3乗の展開公式を利用しよう。
\begin{align*}
(\sqrt{5}-i)^3&=5\sqrt{5}+3(\sqrt{5})^2\Cdota(-i)+3\Cdota\sqrt{5}(-i)^2+(-i)^3 \\[4pt]
&=5\sqrt{5}-15i-3\sqrt{5}+i \\[4pt]
&=2\sqrt{5}+(-14)i
\end{align*}
(\sqrt{5}-i)^3&=5\sqrt{5}+3(\sqrt{5})^2\Cdota(-i)+3\Cdota\sqrt{5}(-i)^2+(-i)^3 \\[4pt]
&=5\sqrt{5}-15i-3\sqrt{5}+i \\[4pt]
&=2\sqrt{5}+(-14)i
\end{align*}
複素数の除法【千葉工業大】
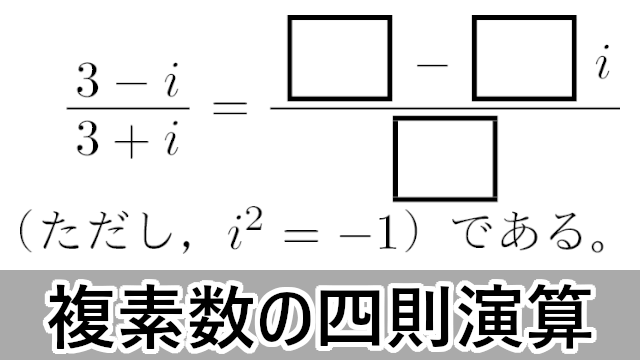
2016年 千葉工業大$\dfrac{3-i}{3+i}=\dfrac{\myhako-\myhako\,i}{\myhako}$(ただし,$i^2=-1$)である。

ヒロ
分母が無理数のときは「分母の有理化」を行ったが,同じように,分母が複素数のときは「分母の実数化」をしよう。
共役な複素数複素数 $z=a+bi$($a,~b$ は実数)に対して,$a-bi$ を $a+bi$ の共役な複素数といい,$\overline{z}$ で表す。
【考え方と解答】
分母を実数化するときは,分母分子に共役な複素数を掛けると良い。
分母を実数化するときは,分母分子に共役な複素数を掛けると良い。
\begin{align*}
\dfrac{3-i}{3+i}&=\dfrac{3-i}{3+i}\times\dfrac{3-i}{3-i} \\[4pt]
&=\dfrac{9-6i+i^2}{9-i^2} \\[4pt]
&=\dfrac{8-6i}{10}=\dfrac{4-3i}{5}
\end{align*}
\dfrac{3-i}{3+i}&=\dfrac{3-i}{3+i}\times\dfrac{3-i}{3-i} \\[4pt]
&=\dfrac{9-6i+i^2}{9-i^2} \\[4pt]
&=\dfrac{8-6i}{10}=\dfrac{4-3i}{5}
\end{align*}