ここでは平面ベクトルと三角形の面積について解説します。
三角形の面積はこれまでに様々な単元で出題されていますが,ベクトルの単元でも出題されます。
大学によっては,三角形の面積の公式を証明させる問題が出題される場合もあるため,公式の成り立ちも理解していつでも導出できるようにしておくことが重要です。
Contents
三角形の面積公式

ヒロ
まずは三角形の面積をベクトルを用いて表せるようにしておこう。
三角形の面積公式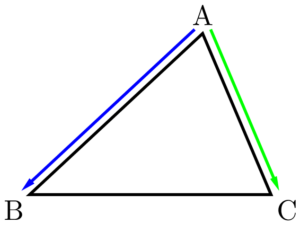
三角形ABCの面積は次のように表すことができる。

三角形ABCの面積は次のように表すことができる。
\begin{align*} \sankaku{ABC}=\dfrac{1}{2}\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2} \end{align*}

ヒロ
公式の証明は次のようになる。
【三角形の面積公式】
$\kaku{BAC}=A$ とすると,三角形ABCの面積 $S$ は次のようになる。
\begin{align*}
S=\dfrac{1}{2}\abs{\Vec{AB}}\abs{\Vec{AC}}\sin A~\cdots\cdots①
\end{align*}
ここで $\cos A=\dfrac{\Vec{AB}\Cdot\Vec{AC}}{\abs{\Vec{AB}}\abs{\Vec{AC}}}$ であるからS=\dfrac{1}{2}\abs{\Vec{AB}}\abs{\Vec{AC}}\sin A~\cdots\cdots①
\end{align*}
\begin{align*}
\sin A&=\sqrt{1-\cos^2A} \\[4pt]
&=\sqrt{1-\left(\dfrac{\Vec{AB}\Cdot\Vec{AC}}{\abs{\Vec{AB}}\abs{\Vec{AC}}}\right)^2} \\[4pt]
&=\dfrac{\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2}}{\abs{\Vec{AB}}\abs{\Vec{AC}}}
\end{align*}
①に代入すると\sin A&=\sqrt{1-\cos^2A} \\[4pt]
&=\sqrt{1-\left(\dfrac{\Vec{AB}\Cdot\Vec{AC}}{\abs{\Vec{AB}}\abs{\Vec{AC}}}\right)^2} \\[4pt]
&=\dfrac{\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2}}{\abs{\Vec{AB}}\abs{\Vec{AC}}}
\end{align*}
\begin{align*}
S&=\dfrac{1}{2}\abs{\Vec{AB}}\abs{\Vec{AC}}\Cdot\dfrac{\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2}}{\abs{\Vec{AB}}\abs{\Vec{AC}}} \\[4pt]
&=\dfrac{1}{2}\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2}
\end{align*}
S&=\dfrac{1}{2}\abs{\Vec{AB}}\abs{\Vec{AC}}\Cdot\dfrac{\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2}}{\abs{\Vec{AB}}\abs{\Vec{AC}}} \\[4pt]
&=\dfrac{1}{2}\sqrt{\abs{\Vec{AB}}^2\abs{\Vec{AC}}^2-(\Vec{AB}\Cdot\Vec{AC})^2}
\end{align*}
2022年 中央大
2022年 中央大点Oを中心とする半径 $r$ の円 $O$ の周上に中心角 $\dfrac{2}{3}\pi$ の弧ABをとる。
このとき,半円より大きい方の弧ABの上に点Cを,弦の長さの比が$\textrm{AC}:\textrm{BC}=3:1$ となるようにとる。次を求めよ。
(1) 弦ACの長さ
(2) 平面ベクトルの内積 $\Vec{OA}\Cdot\Vec{OC}$
(3) $\sankaku{AOC}$ の面積
このとき,半円より大きい方の弧ABの上に点Cを,弦の長さの比が$\textrm{AC}:\textrm{BC}=3:1$ となるようにとる。次を求めよ。
(1) 弦ACの長さ
(2) 平面ベクトルの内積 $\Vec{OA}\Cdot\Vec{OC}$
(3) $\sankaku{AOC}$ の面積
【(1)の解答と考え方】
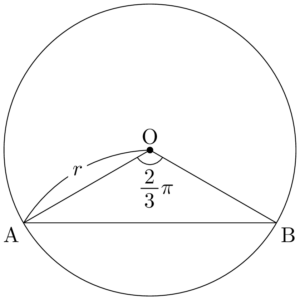
まずは図を描いて状況を把握しよう。中心角が$\dfrac{2}{3}\pi$だから$\kaku{ACB}=\dfrac{\pi}{3}$となる。「円に内接する正三角形を描く方法」を利用して,円と三角形OABを描こう。
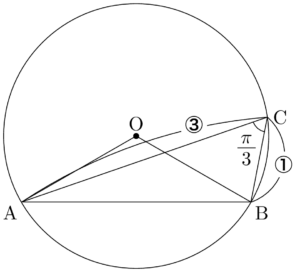
次に点Cをとる。点Cは「半円より大きい方の弧AB上にある」と書かれているから,点Cは弦ABに対して点Oと同じ側にあることが分かる。$\textrm{AC}:\textrm{BC}=3:1$になるように点Cをとると次のようになる。ここで円周角と中心角の関係から$\kaku{ACB}=\dfrac{\pi}{3}$になるから図に書き込んでおこう。
辺の長さを求める場合,その辺を含む三角形に着目するのが基本である。ACの長さを求めたいから三角形ABCに着目する。$\textrm{AC}:\textrm{BC}=3:1$だから,$\textrm{BC}=x$とおくと,$\textrm{AC}=3x$と表せる。あとはABの長さが分かれば三角形ABCにおいて余弦定理を使うことで$x$を求めることができる。
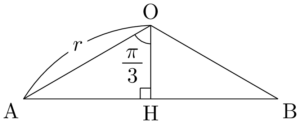
ABの長さを求めるために,三角形OABに着目する。二等辺三角形の底辺を求めることになるから,頂点Oから垂線OHを下ろしてABの長さを求めよう。
三角形OAHが直角三角形だから
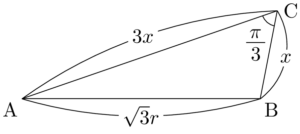
三角形ABCにおいて余弦定理を用いると
まずは図を描いて状況を把握しよう。中心角が$\dfrac{2}{3}\pi$だから$\kaku{ACB}=\dfrac{\pi}{3}$となる。「円に内接する正三角形を描く方法」を利用して,円と三角形OABを描こう。

次に点Cをとる。点Cは「半円より大きい方の弧AB上にある」と書かれているから,点Cは弦ABに対して点Oと同じ側にあることが分かる。$\textrm{AC}:\textrm{BC}=3:1$になるように点Cをとると次のようになる。ここで円周角と中心角の関係から$\kaku{ACB}=\dfrac{\pi}{3}$になるから図に書き込んでおこう。

辺の長さを求める場合,その辺を含む三角形に着目するのが基本である。ACの長さを求めたいから三角形ABCに着目する。$\textrm{AC}:\textrm{BC}=3:1$だから,$\textrm{BC}=x$とおくと,$\textrm{AC}=3x$と表せる。あとはABの長さが分かれば三角形ABCにおいて余弦定理を使うことで$x$を求めることができる。
ABの長さを求めるために,三角形OABに着目する。二等辺三角形の底辺を求めることになるから,頂点Oから垂線OHを下ろしてABの長さを求めよう。

三角形OAHが直角三角形だから
\begin{align*}
\textrm{AB}&=2\textrm{AH} \\[4pt]
&=2\textrm{OA}\sin\dfrac{\pi}{3} \\[4pt]
&=2r\Cdot\dfrac{\sqrt{3}}{2}=\sqrt{3}r
\end{align*}
それではACの長さを求めよう。\textrm{AB}&=2\textrm{AH} \\[4pt]
&=2\textrm{OA}\sin\dfrac{\pi}{3} \\[4pt]
&=2r\Cdot\dfrac{\sqrt{3}}{2}=\sqrt{3}r
\end{align*}

三角形ABCにおいて余弦定理を用いると
\begin{align*}
&(\sqrt{3}r)^2=(3x)^2+x^2-2\Cdot3x\Cdot x\cos\dfrac{\pi}{3} \\[4pt]
&3r^2=9x^2+x^2-3x^2 \\[4pt]
&7x^2=3r^2 \\[4pt]
&x=\dfrac{\sqrt{3}}{\sqrt{7}}r=\dfrac{\sqrt{21}}{7}r
\end{align*}
$\textrm{AC}=3x$より,求めるACの長さは$\dfrac{3\sqrt{21}}{7}r$&(\sqrt{3}r)^2=(3x)^2+x^2-2\Cdot3x\Cdot x\cos\dfrac{\pi}{3} \\[4pt]
&3r^2=9x^2+x^2-3x^2 \\[4pt]
&7x^2=3r^2 \\[4pt]
&x=\dfrac{\sqrt{3}}{\sqrt{7}}r=\dfrac{\sqrt{21}}{7}r
\end{align*}

ヒロ
ベクトルを利用せずに解いてしまったが,そういうこともある。(2)を見て扱っている単元がベクトルと分かるが,ベクトルに固執する必要はない。知っている知識を活用して,できるだけ短時間で解けるようにすることが重要である。

ヒロ
ちなみに$2:3:\sqrt{7}$の「ルナ三角形」を知っていればACの長さをすぐに求めることができる。

ヒロ
次の(2)の内積を求める問題では,次の公式が役に立つ。
三角形の3辺の長さと内積の関係下の図において,

\begin{align*}
\Vec{AB}\Cdot\Vec{AC}=\dfrac{\textrm{AB}^2+\textrm{AC}^2-\textrm{BC}^2}{2}
\end{align*}
が成り立つ。\Vec{AB}\Cdot\Vec{AC}=\dfrac{\textrm{AB}^2+\textrm{AC}^2-\textrm{BC}^2}{2}
\end{align*}


ヒロ
証明は次のようになる。
【証明】
余弦定理を考えると
\begin{align*}
\textrm{BC}^2=\textrm{AB}^2+\textrm{AC}^2-2\textrm{AB}\Cdot\textrm{AC}\cos\kaku{BAC}
\end{align*}
であり,$\textrm{AB}\Cdot\textrm{AC}\cos\kaku{BAC}=\Vec{AB}\Cdot\Vec{AC}$であるから\textrm{BC}^2=\textrm{AB}^2+\textrm{AC}^2-2\textrm{AB}\Cdot\textrm{AC}\cos\kaku{BAC}
\end{align*}
\begin{align*}
&\textrm{BC}^2=\textrm{AB}^2+\textrm{AC}^2-2\Vec{AB}\Cdot\Vec{AC} \\[4pt]
&\Vec{AB}\Cdot\Vec{AC}=\dfrac{\textrm{AB}^2+\textrm{AC}^2-\textrm{BC}^2}{2}
\end{align*}
&\textrm{BC}^2=\textrm{AB}^2+\textrm{AC}^2-2\Vec{AB}\Cdot\Vec{AC} \\[4pt]
&\Vec{AB}\Cdot\Vec{AC}=\dfrac{\textrm{AB}^2+\textrm{AC}^2-\textrm{BC}^2}{2}
\end{align*}
【(2)の解答と考え方】
$\textrm{OA}=\textrm{OC}=r$,$\textrm{AC}=\dfrac{3\sqrt{3}}{\sqrt{7}}r$であるから
$\textrm{OA}=\textrm{OC}=r$,$\textrm{AC}=\dfrac{3\sqrt{3}}{\sqrt{7}}r$であるから
\begin{align*}
\Vec{OA}\Cdot\Vec{OC}&=\dfrac{\textrm{OA}^2+\textrm{OC}^2-\textrm{AC}^2}{2} \\[4pt]
&=\dfrac{r^2+r^2-\dfrac{27}{7}r^2}{2} \\[4pt]
&=-\dfrac{13}{14}r^2
\end{align*}
\Vec{OA}\Cdot\Vec{OC}&=\dfrac{\textrm{OA}^2+\textrm{OC}^2-\textrm{AC}^2}{2} \\[4pt]
&=\dfrac{r^2+r^2-\dfrac{27}{7}r^2}{2} \\[4pt]
&=-\dfrac{13}{14}r^2
\end{align*}

ヒロ
最後の三角形AOCの面積は公式を利用して求めよう。
【(3)の解答と考え方】
三角形AOCの面積は
三角形AOCの面積は
\begin{align*}
&\dfrac{1}{2}\sqrt{\textrm{OA}^2\Cdot\textrm{OC}^2-(\Vec{OA}\Cdot\Vec{OC})^2} \\[4pt]
&=\dfrac{1}{2}\sqrt{r^2\Cdot r^2-\left(-\dfrac{13}{14}r^2\right)^2} \\[4pt]
&=\dfrac{1}{2}\Cdot\dfrac{\sqrt{14^2-13^2}}{14}r^2 \\[4pt]
&=\dfrac{3\sqrt{3}}{28}r^2
\end{align*}
&\dfrac{1}{2}\sqrt{\textrm{OA}^2\Cdot\textrm{OC}^2-(\Vec{OA}\Cdot\Vec{OC})^2} \\[4pt]
&=\dfrac{1}{2}\sqrt{r^2\Cdot r^2-\left(-\dfrac{13}{14}r^2\right)^2} \\[4pt]
&=\dfrac{1}{2}\Cdot\dfrac{\sqrt{14^2-13^2}}{14}r^2 \\[4pt]
&=\dfrac{3\sqrt{3}}{28}r^2
\end{align*}


















