ここでは2次関数のグラフがx軸から切り取る線分の長さについて説明します。
単純な問題ですが,良く出る問題なので,確実に解けるようにしておきましょう。
また,解けるようにするだけでなく,速く解くことを重視する場合は時短解法が有効です。
時短解法を知っていると,私大入試によく見られるマーク式試験では有利になります。
Contents
2次関数のグラフが $x$ 軸から切り取る線分の長さ

ヒロ
まずは,言葉が指す線分がどの線分であるかを知ろう。
【放物線が $x$ 軸から切り取る線分】
放物線が $x$ 軸から切り取る線分とは,次の図において赤線で表した線分ABのことである。
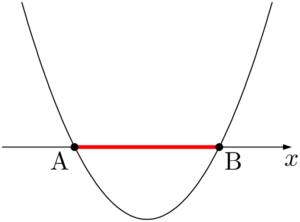
$x$ 軸を麺とみて,放物線状の金型で切り取ると考えると良いかもしれない。
※「$x$ 軸が放物線によって切り取られる線分」と言われることもある。
放物線が $x$ 軸から切り取る線分とは,次の図において赤線で表した線分ABのことである。

$x$ 軸を麺とみて,放物線状の金型で切り取ると考えると良いかもしれない。
※「$x$ 軸が放物線によって切り取られる線分」と言われることもある。

ヒロ
次に放物線が $x$ 軸から切り取る線分の長さの求め方を知ろう。
【放物線が $x$ 軸から切り取る線分の長さの求め方】
次の図のように放物線 $C:y=ax^2+bx+c~(a>0)$ が $x$ 軸と2点A, Bで交わっているとする。
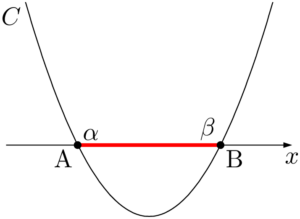
2点A, Bの $x$ 座標をそれぞれ $\alpha,~\beta$ とすると,放物線 $C$ が $x$ 軸から切り取る線分の長さは
$D=b^2-4ac$ として,$ax^2+bx+c=0$ を解くと,$x=\dfrac{-b\pm\sqrt{D}}{2a}$ となるから,
次の図のように放物線 $C:y=ax^2+bx+c~(a>0)$ が $x$ 軸と2点A, Bで交わっているとする。

2点A, Bの $x$ 座標をそれぞれ $\alpha,~\beta$ とすると,放物線 $C$ が $x$ 軸から切り取る線分の長さは
\begin{align*}
\text{AB}=\beta-\alpha
\end{align*}
と表される。\text{AB}=\beta-\alpha
\end{align*}
$D=b^2-4ac$ として,$ax^2+bx+c=0$ を解くと,$x=\dfrac{-b\pm\sqrt{D}}{2a}$ となるから,
\begin{align*}
\text{AB}&=\dfrac{-b+\sqrt{D}}{2a}-\dfrac{-b-\sqrt{D}}{2a} \\[4pt]
&=\dfrac{\sqrt{D}}{a}
\end{align*}
グラフが上に凸になるとき,$a<0$ となるため,$a$ の符号が正でも負でもどちらでも対応できるように1つの式で表すと \text{AB}&=\dfrac{-b+\sqrt{D}}{2a}-\dfrac{-b-\sqrt{D}}{2a} \\[4pt]
&=\dfrac{\sqrt{D}}{a}
\end{align*}
\begin{align*} \text{AB}=\dfrac{\sqrt{D}}{\abs{a}} \end{align*}
となる。私大入試によく見られるマーク式試験では,この式を利用することで時短することができる。2次関数のグラフが $x$ 軸から切り取る線分の長さに関する問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題2次関数 $y=x^2-4x+2$ のグラフが $x$ 軸から切り取る線分の長さを求めよ。
【考え方と解答】
放物線と $x$ 軸の交点の $x$ 座標を求める。
$x^2-4x+2=0$ より $x=2\pm\sqrt{2}$
よって,求める線分の長さは
放物線と $x$ 軸の交点の $x$ 座標を求める。
$x^2-4x+2=0$ より $x=2\pm\sqrt{2}$
よって,求める線分の長さは
\begin{align*}
(2+\sqrt{2})-(2-\sqrt{2})=2\sqrt{2}
\end{align*}
(2+\sqrt{2})-(2-\sqrt{2})=2\sqrt{2}
\end{align*}
2次関数のグラフが $x$ 軸から切り取る線分の長さに関する入試問題

ヒロ
2019年に昭和大学で出題された問題を解いてみよう。
2019年 昭和大(改)$x$ の2次関数 $y=x^2-2mx+4m+3$ のグラフが $x$ 軸から切り取る線分の長さが6であるとき,$m$ の値とそのときの $x$ 軸との共有点の $x$ 座標を求めよ。
【考え方と解答】
$x^2-2mx+4m+3=0\cdots\cdots①$ の判別式を $D$ とすると
$m=6$ のとき,$x=3,~9$
$m=-2$ のとき,$x=-5,~1$
$x^2-2mx+4m+3=0\cdots\cdots①$ の判別式を $D$ とすると
\begin{align*}
\dfrac{D}{4}&=m^2-(4m+3) \\[4pt]
&=m^2-4m-3
\end{align*}
2次関数 $y=x^2-2mx+4m+3$ のグラフが $x$ 軸から切り取る線分の長さが6のとき,\dfrac{D}{4}&=m^2-(4m+3) \\[4pt]
&=m^2-4m-3
\end{align*}
\begin{align*}
&\sqrt{D}=6 \\[4pt]
&D=36 \\[4pt]
&\dfrac{D}{4}=9
\end{align*}
であるから&\sqrt{D}=6 \\[4pt]
&D=36 \\[4pt]
&\dfrac{D}{4}=9
\end{align*}
\begin{align*}
&m^2-4m-3=9 \\[4pt]
&m^2-4m-12=0 \\[4pt]
&(m-6)(m+2)=0 \\[4pt]
&m=6,~-2
\end{align*}
①の2解は $x=m\pm\sqrt{\dfrac{D}{4}}=m\pm3$ であるから,&m^2-4m-3=9 \\[4pt]
&m^2-4m-12=0 \\[4pt]
&(m-6)(m+2)=0 \\[4pt]
&m=6,~-2
\end{align*}
$m=6$ のとき,$x=3,~9$
$m=-2$ のとき,$x=-5,~1$