2019年センター試験 数学ⅠA 第5問 平面図形の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
このとき,$\cos\kaku{BAC}=-\dfrac{1}{5}$, $\sin\kaku{BAC}=\dfrac{2\sqrt{6}}{5}$ である。
$\sankaku{ABC}$ の内接円の半径は $\dfrac{\sqrt{\myBox{ア}}}{\myBox{イ}}$ である。
この内接円と辺ABとの接点をD,辺ACとの接点をEとする。
\mathrm{AD}=\myBox{ウ},~\mathrm{DE}=\dfrac{\myBox{エ}\sqrt{\myBox{オカ}}}{\myBox{キ}}
\end{align*}
線分BEと線分CDの交点をP,直線APと辺BCの交点をQとする。
\dfrac{\mathrm{BQ}}{\mathrm{CQ}}=\dfrac{\myBox{ク}}{\myBox{ケ}}
\end{align*}
\mathrm{IQ}=\dfrac{\sqrt{\myBox{サ}}}{\myBox{シ}}
\end{align*}
\cos\kaku{DFE}=\dfrac{\sqrt{\myBox{スセ}}}{\myBox{ソ}}
\end{align*}
考え方と解答

最初は内接円の半径を求める問題。

$\sankaku{ABC}$ の3辺の長さが与えられていて,$\sin A$ の値も分かっているから,面積を利用すれば大丈夫だね。
$\sankaku{ABC}$ の内接円の半径を $r$ とすると
&\dfrac{1}{2}(\mathrm{AB}+\mathrm{BC}+\mathrm{CA})r=\dfrac{1}{2}\Cdota\mathrm{AB}\Cdota\mathrm{AC}\sin A \\[4pt]
&(4+7+5)r=4\Cdota5\Cdota\dfrac{2\sqrt{6}}{5} \\[4pt]
&r=\dfrac{4\Cdot5\Cdot2\sqrt{6}}{5\Cdot16} \\[4pt]
&r=\dfrac{\sqrt{6}}{2}
\end{align*}

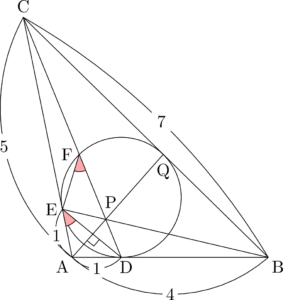
$\cos\kaku{BAC}=-\dfrac{1}{5}$ で,$\mathrm{AC}=5$ だから,うまく利用して図を描いておこう。
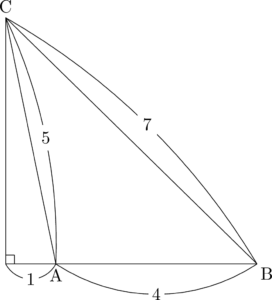

今回はそんなに丁寧に描く必要はなさそうだけどね。

内接円を描いて,ADとDEの長さを求めよう。
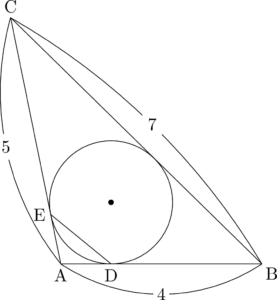
ADとAEは点Aから内接円に引いた接線の長さだから,
\mathrm{AD}&=\dfrac{\mathrm{AB}+\mathrm{AC}-\mathrm{BC}}{2} \\[4pt]
&=\dfrac{4+5-7}{2} \\[4pt]
&=1
\end{align*}
\mathrm{DE}^2&=\mathrm{AD}^2+\mathrm{AE}^2-2\Cdota\mathrm{AD}\Cdota\mathrm{AE}\cos\kaku{BAC} \\[4pt]
&=1^2+1^2-2\Cdota1\Cdota1\Cdota\left(-\dfrac{1}{5}\right) \\[4pt]
&=\dfrac{12}{5}
\end{align*}
\mathrm{DE}=\dfrac{2\sqrt{3}}{\sqrt{5}}=\dfrac{2\sqrt{15}}{5}
\end{align*}

個人的に接線の長さを求める式を公式として覚えているが,覚えるか覚えないかについてはどちらでもよい。普通に解いて間に合うのなら覚える必要はない。

時間が足りない人は,覚えて使えるようにして時間短縮しよう。

次は辺の長さの比を求める問題。とりあえず図を描いて2点P, Qの位置を把握しよう。
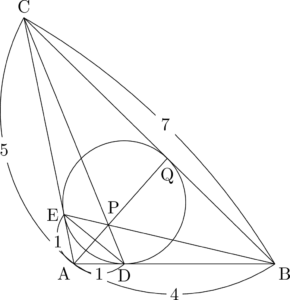

チェバの定理を使えば求められるね。間違っても,CQとBQの長さを求めて分数にすれば良いと考えてはいけない。
チェバの定理より
&\dfrac{\mathrm{BQ}}{\mathrm{QC}}\Cdota\dfrac{\mathrm{CE}}{\mathrm{EA}}\Cdota\dfrac{\mathrm{AD}}{\mathrm{DB}}=1 \\[4pt]
&\dfrac{\mathrm{BQ}}{\mathrm{QC}}\Cdota\dfrac{4}{1}\Cdota\dfrac{1}{3}=1 \\[4pt]
&\dfrac{\mathrm{BQ}}{\mathrm{QC}}=\dfrac{3}{4}
\end{align*}

次はBQの長さを求める問題。いま求めた辺の比とBCの長さを利用しよう。
$\mathrm{BQ}:\mathrm{QC}=3:4$ であるから,
\mathrm{BQ}&=\dfrac{3}{7}\mathrm{BC} \\[4pt]
&=\dfrac{3}{7}\Cdota7 \\[4pt]
&=3
\end{align*}

次はIQの長さを求める問題。図では内接円とBCの接点がQに見えるけど,自分で描いた図の見た目はあまり信用できないため,計算で確認しないといけない。
$\mathrm{BQ}=3$ であり,$\mathrm{BD}=3$ であるから,Qは内接円とBCとの接点である。すなわち,IQの長さは内接円の半径に等しいから
\mathrm{IQ}=r=\dfrac{\sqrt{6}}{2}
\end{align*}

次は余弦の値を求める問題。まずは点Fの位置を確認しよう。
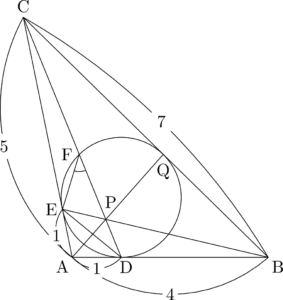

突然現れた円周角の問題では,他に等しい大きさの角がないかチェックするようにしよう。
接弦定理より,$\kaku{DFE}=\kaku{AED}$
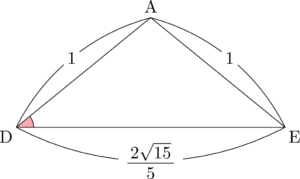
$\sankaku{ADE}$ は $\mathrm{AD}=\mathrm{AE}$ の二等辺三角形である。$\sankaku{ADE}$ を取り出して描くと次のようになる。
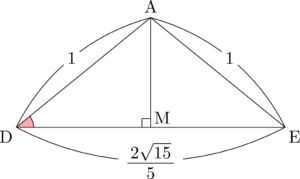
よって,点Aから辺DEに下ろした垂線とDEはDEの中点Mで交わる。
したがって,
\cos\kaku{DFE}&=\cos\kaku{ADM} \\[4pt]
&=\dfrac{\mathrm{DM}}{\mathrm{AD}} \\[4pt]
&=\dfrac{1}{2}\mathrm{DE} \\[4pt]
&=\dfrac{1}{2}\Cdota\dfrac{2\sqrt{15}}{5} \\[4pt]
&=\dfrac{\sqrt{15}}{5}
\end{align*}
別解

ADの長さを求める問題は,通常であれば,次のように解くのだろう。
$\mathrm{AD=AE}=x$ とおくと,
&\mathrm{BD}=4-x,~\mathrm{CE}=5-x
\end{align*}
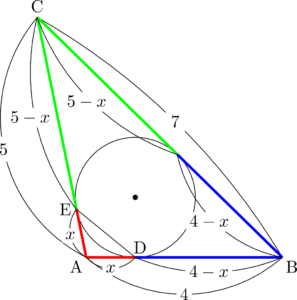
よって
&(5-x)+(4-x)=7 \\[4pt]
&x=\dfrac{5+4-7}{2}=1
\end{align*}

この過程をその都度繰り返しても良いが,2016年のセンターⅠA追試のように,連続して3問も出題されると,その都度考えるのが面倒になる。「接線の長さ」を公式として覚えてしまえば,機械的に次々と問題を解くことができる。

覚えたい人は覚えよう。覚えたくない人は覚えなくても良い。あなたにとって,これを公式とした方が良いかどうかを考えて行動しよう。

また,三角関数の各種公式を利用できる人は,どんどん利用すれば良い。

例えばDEの長さを求める問題では,次のように求めることもできる。
内心をI,$\kaku{IAE}=\theta$ とする。
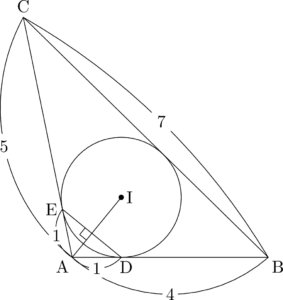
$\theta=\dfrac{1}{2}\kaku{BAC}$ であるから,
\sin\theta&=\sqrt{\dfrac{1-\cos2\theta}{2}} \\[4pt]
&=\sqrt{\dfrac{1-\cos\kaku{BAC}}{2}} \\[4pt]
&=\sqrt{\dfrac{1-\left(-\dfrac{1}{5}\right)}{2}} \\[4pt]
&=\sqrt{\dfrac{3}{5}} \\[4pt]
&=\dfrac{\sqrt{15}}{5}
\end{align*}
\mathrm{DE}&=2\sin\theta \\[4pt]
&=\dfrac{2\sqrt{15}}{5}
\end{align*}

四角形ADIEの面積に着目することでもDEの長さを求めることができる。
三平方の定理より
\mathrm{AI}&=\sqrt{1^2+\left(\dfrac{\sqrt{6}}{2}\right)^2} \\[4pt]
&=\dfrac{\sqrt{10}}{2}
\end{align*}
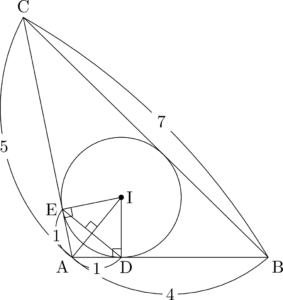
四角形ADIEの面積を考えて
&\sankaku{ADI}+\sankaku{AEI}=\dfrac{1}{2}\Cdota\mathrm{AI}\Cdota\mathrm{DE} \\[4pt]
&2\times\dfrac{1}{2}\Cdota1\Cdota\dfrac{\sqrt{6}}{2}=\dfrac{1}{2}\Cdota\dfrac{\sqrt{10}}{2}\Cdota\mathrm{DE} \\[4pt]
&\mathrm{DE}=\dfrac{2\sqrt{6}}{\sqrt{10}}=\dfrac{2\sqrt{15}}{5}
\end{align*}

DEの長さを求めるときに,AIの長さを求めている人は,最後の $\cos\kaku{DFE}$ の値を求めるときに少し楽になる。
中心角が円周角の2倍であることと,AIが $\kaku{DIE}$ の二等分線になっていることを考えると,
\kaku{DFE}=\kaku{AID}
\end{align*}
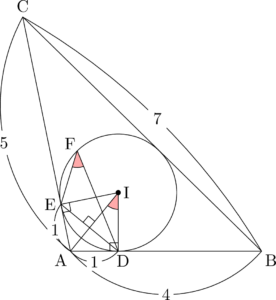
$\sankaku{AID}$ は直角三角形であるから
\cos\kaku{DFE}&=\cos\kaku{AID} \\[4pt]
&=\dfrac{\mathrm{ID}}{\mathrm{AI}} \\[4pt]
&=\dfrac{\dfrac{\sqrt{6}}{2}}{\dfrac{\sqrt{10}}{2}} \\[4pt]
&=\dfrac{\sqrt{3}}{\sqrt{5}}=\dfrac{\sqrt{15}}{5}
\end{align*}

他の方法としては,正弦定理を利用しようとする人もいるかもしれない。

それは $\sankaku{DFE}$ が $\sankaku{ABC}$ の内接円に内接する三角形である,すなわち,$\sankaku{ABC}$ の内接円が $\sankaku{DFE}$ の外接円になることを考える方法である。

少々遠回りになるが,その方法でも解けるので,$\sin$ や $\cos$ の違いを気にせずにどんどん計算しよう。
$\sankaku{ABC}$ の内接円は $\sankaku{DEF}$ の外接円であるから,正弦定理より
\sin\kaku{DFE}&=\dfrac{\mathrm{DE}}{2r} \\[4pt]
&=\dfrac{2\sqrt{3}}{\sqrt{5}}\Cdota\dfrac{1}{2\Cdot\dfrac{\sqrt{6}}{2}} \\[4pt]
&=\dfrac{2}{\sqrt{10}}=\dfrac{\sqrt{2}}{\sqrt{5}}
\end{align*}
\sin\kaku{DFE}&=\sqrt{1-\left(\dfrac{\sqrt{2}}{\sqrt{5}}\right)^2} \\[4pt]
&=\dfrac{\sqrt{3}}{\sqrt{5}} \\[4pt]
&=\dfrac{\sqrt{15}}{5}
\end{align*}
2019年 センター数学ⅠA 平面図形を解いた感想

三角比の値を利用することで,かなり正確な図を描くことができるが,この問題ではほとんどメリットはなかった。

内接円の半径を求めるときに,三角形の面積を利用するのは有名な方法なので覚えておこう。

DEの長さや $\cos\kaku{DFE}$ を求めるときには,数学Ⅱの三角関数の2倍角の公式などを利用する解法もある。「数学ⅠAの範囲で考えなければならない」ということはなく,知っているもので利用できるものはすべて利用するという姿勢も重要である。




















