2020年センター試験 数学ⅡB 第2問 微積

2020年センター試験数学ⅡB 第2問微積の解説をします。

まだ問題を解いていない人は解いてから解説を読んでください。

2020年センターⅡB 第2問微積　$a>0$ とし，$f(x)=x^2-(4a-2)x+4a^2+1$ とおく。座標平面上で，放物線 $y=x^2+2x+1$ を $C$，放物線 $y=f(x)$ を $D$ とする。また，$\ell$ を $C$ と $D$ の両方に接する直線とする。
(1) $\ell$ の方程式を求めよう。
　$\ell$ と $C$ は点 $(t,~t^2+2t+1)$ において接するとすると，$\ell$ の方程式は

\begin{align*}
y=\left(\myBox{ア}\,t+\myBox{イ}\right)x-t^2+\myBox{ウ}~\cdots\cdots①
\end{align*}

である。また，$\ell$ と $D$ は点 $(s,~f(s))$ において接するとすると，
$\ell$ の方程式は

\begin{align*}
y&=\left(\myBox{エ}\,s-\myBox{オ}\,a+\myBox{カ}\right)x \\[4pt]
&　　　　-s^2+\myBox{キ}\,a^2+\myBox{ク}~\cdots\cdots②
\end{align*}

である。ここで，①と②は同じ直線を表しているので，
$t=\myBox{ケ}$, $s=\myBox{コ}\,a$ が成り立つ。
　したがって，$\ell$ の方程式は $y=\myBox{サ}\,x+\myBox{シ}$ である。
(2) 二つの放物線 $C,~D$ の交点の $x$ 座標は $\myBox{ス}$ である。
　$C$ と直線 $\ell$，および直線 $x=\mybox{ス}$ で囲まれた図形の面積を $S$ とすると，
$S=\dfrac{a^{\myBox{セ}}}{\myBox{ソ}}$ である。
(3) $a\geqq\dfrac{1}{2}$ とする。二つの放物線 $C,~D$ と直線 $\ell$ で囲まれた図形の中で $0\leqq x\leqq1$ を満たす部分の面積 $T$ は，$a>\myBox{タ}$ のとき，$a$ の値によらず

\begin{align*}
T=\dfrac{\myBox{チ}}{\myBox{ツ}}
\end{align*}

であり，$\dfrac{1}{2}\leqq a\leqq\mybox{タ}$ のとき

\begin{align*}
T=-\myBox{テ}\,a^3+\myBox{ト}\,a^2-\myBox{ナ}\,a+\dfrac{\myBox{ニ}}{\myBox{ヌ}}
\end{align*}

である。
(4) 次に，(2)，(3)で定めた $S,~T$ に対して，$U=2T-3S$ とおく。$a$ が $\dfrac{1}{2}\leqq a\leqq\mybox{タ}$ の範囲を動くとき，$U$ は $a=\dfrac{\myBox{ネ}}{\myBox{ノ}}$ で最大値 $\dfrac{\myBox{ハ}}{\myBox{ヒフ}}$ をとる。

Contents

1 (1)の考え方と解答
2 (2)の考え方と解答
3 (3)の考え方と解答
4 (4)の考え方と解答
5 2020年センター数学ⅡB 微積を解いた感想

(1)の考え方と解答

ヒロ

接点の座標から接線を求める問題。

ヒロ

2次関数のグラフがもつ2乗に比例する性質を利用して一発で接線の方程式を求めよう。

【ア～ウの解答】
$y=x^2+2x+1$ より，$y’=2x+2$ であるから，$\ell$ の方程式は

\begin{align*}
y=(2t+2)x-t^2+1~\cdots\cdots①
\end{align*}

ヒロ

同じように求めよう。

【エ～クの解答】
$f(x)=x^2-(4a-2)x+4a^2+1$ より，$f'(x)=2x-(4a-2)$ であるから，$\ell$ の方程式は

\begin{align*}
y=(2s-4a+2)x-s^2+4a^2+1~\cdots\cdots②
\end{align*}

ヒロ

①と②が同じ直線であることから，$t$ と $s$ を決定する問題。

ヒロ

$x$ の係数と定数項が等しくなるときだから，連立方程式を解けば良いけど，面倒そうなので別の方法で解こう。

ヒロ

$x^2$ の係数が等しいから，共通接線 $\ell$ の傾きは2つの放物線 $C,~D$ の頂点を通る直線の傾きに等しいことを利用しよう。

【ケコの解答】
2つの放物線 $C,~D$ の頂点の座標はそれぞれ

\begin{align*}
(-1,~0),~(2a-1,~4a)
\end{align*}

となるから，2つの頂点を通る直線の傾きは2である。
①より

\begin{align*}
&2t+2=2 \\[4pt]
&t=0
\end{align*}

②より

\begin{align*}
&2s-4a+2=2 \\[4pt]
&s=2a
\end{align*}

ヒロ

$\ell$ の方程式を求めよう。

【サシの方程式】
①に $t=0$ を代入して，$y=2x+1$

(2)の考え方と解答

(2) 二つの放物線 $C,~D$ の交点の $x$ 座標は $\myBox{ス}$ である。
　$C$ と直線 $\ell$，および直線 $x=\mybox{ス}$ で囲まれた図形の面積を $S$ とすると，
$S=\dfrac{a^{\myBox{セ}}}{\myBox{ソ}}$ である。

ヒロ

$x^2$ の係数が等しい二つの放物線の交点の $x$ 座標は，二つの放物線の共通接線との接点の $x$ 座標の平均に等しいことを利用しよう。

【スの解答】
2つの放物線 $C,~D$ と $\ell$ との接点の $x$ 座標は，$0,~2a$ であるから，$C,~D$ の交点の $x$ 座標は

\begin{align*}
\dfrac{0+2a}{2}=a
\end{align*}

ヒロ

放物線・接線・$y$ 軸に平行な直線で囲まれる図形の面積は $\dfrac{1}{3}$ 公式だね。

【セソの解答】
$\ell$ と $C$ の接点($x$ 座標は0)と $x=a$ との距離は $a$ であるから $\dfrac{1}{3}$ 公式より

\begin{align*}
S=\dfrac{a^3}{3}
\end{align*}

ヒロ

ここまでは図を描かずに想像するだけで楽に解けた。

(3)の考え方と解答

(3) $a\geqq\dfrac{1}{2}$ とする。二つの放物線 $C,~D$ と直線 $\ell$ で囲まれた図形の中で $0\leqq x\leqq1$ を満たす部分の面積 $T$ は，$a>\myBox{タ}$ のとき，$a$ の値によらず
\begin{align*}
T=\dfrac{\myBox{チ}}{\myBox{ツ}}
\end{align*}
であり，$\dfrac{1}{2}\leqq a\leqq\mybox{タ}$ のとき
\begin{align*}
T=-\myBox{テ}\,a^3+\myBox{ト}\,a^2-\myBox{ナ}\,a+\dfrac{\myBox{ニ}}{\myBox{ヌ}}
\end{align*}
である。

ヒロ

ここからは図を描こう。

【状況把握のための図】

ヒロ

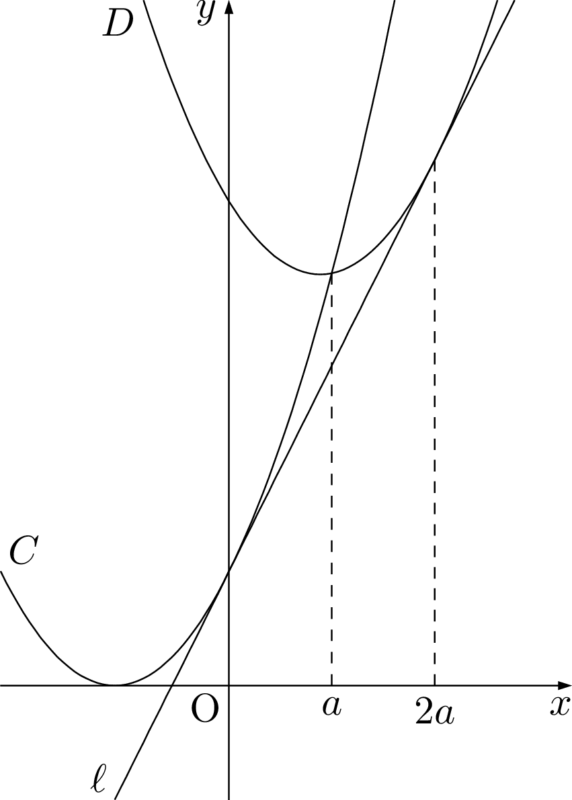
直線 $x=1$ がある位置によって面積 $T$ が変わることを確認しよう。

ヒロ

確認できたらあとは場合分けして答えるだけだね。

【タ～ツの解答】
$a>1$ のときは $a$ の値によらず $T$ は一定である。

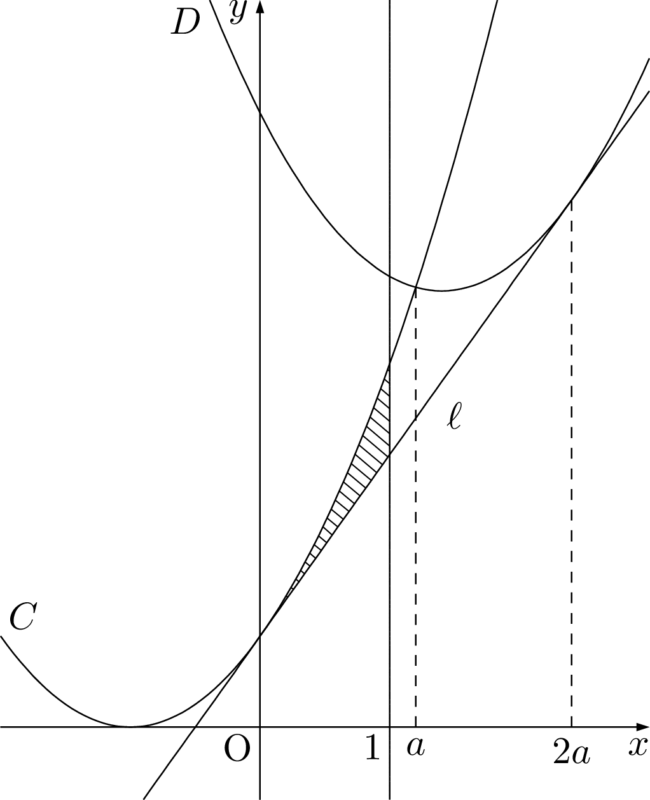
$T$ は $\dfrac{1}{3}$ 公式より，$T=\dfrac{1}{3}$
$a\geqq\dfrac{1}{2}$ より $2a\geqq1$ であるから，直線 $x=1$ が $a\leqq1\leqq2a$ の範囲にあるとき，すなわち $\dfrac{1}{2}\leqq a\leqq1$ のときを考える。

このとき $T$ は上図の斜線部分の面積であるが，緑色で塗った部分を合わせた面積を
$\dfrac{1}{12}$ 公式で簡単に求められることと，緑色で塗った部分の面積は $\dfrac{1}{3}$ 公式で簡単に求められることを利用すると，

\begin{align*}
T&=\dfrac{1}{12}(2a)^3-\dfrac{1}{3}(2a-1)^3 \\[4pt]
&=\dfrac{2}{3}a^3-\left(\dfrac{8}{3}a^3-4a^2+2a-\dfrac{1}{3}\right) \\[4pt]
&=-2a^3+4a^2-2a+\dfrac{1}{3}
\end{align*}

(4)の考え方と解答

(4) 次に，(2)，(3)で定めた $S,~T$ に対して，$U=2T-3S$ とおく。$a$ が $\dfrac{1}{2}\leqq a\leqq\mybox{タ}$ の範囲を動くとき，$U$ は $a=\dfrac{\myBox{ネ}}{\myBox{ノ}}$ で最大値 $\dfrac{\myBox{ハ}}{\myBox{ヒフ}}$ をとる。

ヒロ

$S,~T$ から新たな関数 $U$ の最大値を求める問題。微分して増減を調べよう。

【ネ～フの解答】
$\dfrac{1}{2}\leqq a\leqq1$ のとき

\begin{align*}
U&=2T-3S \\[4pt]
&=2\left(-2a^3+4a^2-2a+\dfrac{1}{3}\right)-3\Cdota\dfrac{a^3}{3} \\[4pt]
&=-5a^3+8a^2-4a+\dfrac{2}{3} \\[4pt]
U’&=-15a^2+16a-4
\end{align*}

$U’=0$ を解くと

\begin{align*}
&15a^2-16a+4=0 \\[4pt]
&(3a-2)(5a-2)=0 \\[4pt]
&a=\dfrac{2}{3},~\dfrac{2}{5}
\end{align*}

$a^3$ の係数が負であるから，$a=\dfrac{2}{5}$ で極小，$a=\dfrac{2}{3}$ で極大となる。$\dfrac{1}{2}\leqq\dfrac{2}{3}\leqq1$ より，$U$ は $a=\dfrac{2}{3}$ で最大値をとる。最大値は

\begin{align*}
U&=2\left\{\dfrac{2}{3}\left(\dfrac{2}{3}\right)^3
-\dfrac{1}{3}\left(\dfrac{1}{3}\right)^3\right\}-\left(\dfrac{2}{3}\right)^3 \\[4pt]
&=\dfrac{1}{3}\left(\dfrac{2}{3}\right)^3
-\dfrac{2}{3}\left(\dfrac{1}{3}\right)^3 \\[4pt]
&=\dfrac{1}{3}\Cdota\dfrac{2^3-2\Cdot1^3}{3^3}=\dfrac{6}{81} \\[4pt]
&=\dfrac{2}{27}
\end{align*}