ここでは経路の総数を求める問題について解説します。
一言で経路の総数を求める問題と言っても,色々ありますが,よくあるのは最短経路の総数ですね。
最短経路の総数を求める問題は得意な人が多いと思いますから,ここでは最短経路ではない経路の総数を求める問題を扱います。
最短経路ではない経路の総数の問題になると,知っているパターンから外れるのでどうすれば良いかが分からなくなるのではないでしょうか?
単純な暗記ではなく,何と何が1対1対応しているのかを見極める力・思考力を鍛えて数学力をアップさせましょう。
2011年 山口大

それでは次の問題を解いてみよう。
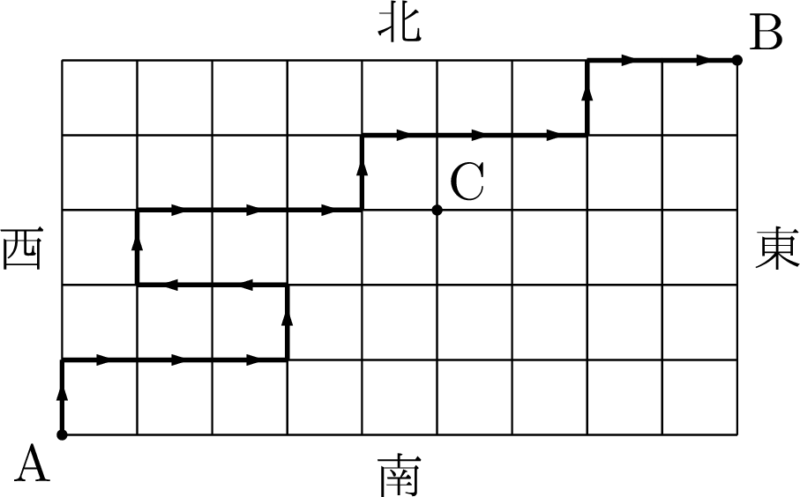
(1) A地点からB地点へ行く道順の総数を求めなさい。
(2) C地点を通って,A地点からB地点へ行く道順の総数を求めなさい。
(3) A地点からB地点まで16区間で行く道順の総数を求めなさい。
(1)の考え方と解答

最短経路の総数を求める問題ではないため,単なる暗記は通用しない。

「何を決めれば経路が1つ決まるのか」を考えよう。

それが分かればその何かを決める方法が何通りあるかを数えれば良いね。

しかし,ぼーっと眺めてるだけだと分かるはずがないので,色々な経路を書いてみよう。

その際に,その経路に決めた原因がどこにあるのか,何を決めたからその経路になったのかを考えるようにしよう。

実はこの作業が最も難しい。上の図の経路であっても,何かを決めているから太線の経路になっている。それを明らかにしよう。
1つの道順は,南北に進む5個の $\uparrow$ をそれぞれ東西の10か所のどこに配置するかにより決まる。この対応は1対1だから,道順の総数は
10^5=100000~通り
\end{align*}

(1)を解けなければ大問丸ごと白紙になる可能性が高い。
(2)の考え方と解答
(2) C地点を通って,A地点からB地点へ行く道順の総数を求めなさい。

(1)を解くことができれば,(2)も解けるだろう。

C地点を通るときの状況で場合分けして考えよう。
南北の通りを西から東に1~10まで番号をつける。5段の東西の区間に対して $\uparrow$ を選ぶ位置を,南から北へ並べて,$(a,~b,~c,~d,~e)$ と表すと,次の3種類が考えられる。
(i) $1\leqq a\leqq10,~1\leqq b\leqq10,~1\leqq c\leqq5
,~6\leqq d\leqq10,~1\leqq e\leqq10$のとき
10\times10\times5\times5\times10=25000
\end{align*}
,~1\leqq d\leqq10,~1\leqq e\leqq10$のとき
10\times10\times1\times10\times10=10000
\end{align*}
,~1\leqq d\leqq6,~1\leqq e\leqq10$のとき
10\times10\times4\times6\times10=24000
\end{align*}
25000+10000+24000=59000~通り
\end{align*}
(3)の考え方と解答
(3) A地点からB地点まで16区間で行く道順の総数を求めなさい。

最短経路だと14区間で行くため,16区間で行くときは2区間分だけ遠回りをすることができる。

最短経路の場合は,$\uparrow$ 5個,$\rightarrow$ 9個の順列であるが,16区間で行くときは,$\rightarrow$ と $\leftarrow$ を1個ずつ追加して考えれば良いことが分かるね。

あとは,はみ出さないような順列を考えるだけだね。
16区間で行く道順は,$\uparrow$ 5個,$\rightarrow$ 10個,$\leftarrow$ 1個の順列で表されるが,$\uparrow\leftarrow\uparrow$ が1塊で現れ,この塊の両側に少なくとも1つ $\rightarrow$ がなければならない。$\uparrow\leftarrow\uparrow$ を□で表すと, $\rightarrow$ 10個,$\uparrow$ 3個,□1個の配列は全部で
\dfrac{14!}{10!3!}=4004~通り
\end{align*}
\Sum{k=0}{3}\nCk{13-k}{3-k}
&=\nCk{13}{3}+\nCk{12}{2}+\nCk{11}{1}+\nCk{10}{0} \\[4pt]
&=286+66+11+1=364~通り
\end{align*}
以上から,求める総数は
4004-364\times2=3276~通り
\end{align*}