Contents
【2013年 三重大】正弦・余弦の3倍角の公式
2013年 三重大$\theta$ を $0<\theta<\dfrac{\pi}{6}$ となる実数とし,平面上に3点 $\mathrm{O}(0,~0)$, $\mathrm{P}(\cos\theta,~\sin\theta)$, $\mathrm{Q}(\cos3\theta,~-\sin3\theta)$ をとる。さらに線分PQと $x$ 軸との交点をRとする。以下の問いに答えよ。
(1) 加法定理を用いて $\cos3\theta$ を $\cos\theta$ だけで表す式を導け。同様に $\sin3\theta$ を $\sin\theta$ だけで表す式を導け。
(2) $\mathrm{PR:RQ}=5:11$ のとき,$\sin\theta,~\cos\theta$ の値を求めよ。
(3) (2)の条件下で $\sankaku{POR}$ の面積を求めよ。
(1) 加法定理を用いて $\cos3\theta$ を $\cos\theta$ だけで表す式を導け。同様に $\sin3\theta$ を $\sin\theta$ だけで表す式を導け。
(2) $\mathrm{PR:RQ}=5:11$ のとき,$\sin\theta,~\cos\theta$ の値を求めよ。
(3) (2)の条件下で $\sankaku{POR}$ の面積を求めよ。

ヒロ
(1)は加法定理から3倍角の公式を導く問題。しっかりできるようにしておこう。

丁寧に計算を進めるだけですね。
【(1)の解答】
\begin{align*}
\cos3\theta&=\cos(2\theta+\theta) \\[4pt]&=\cos2\theta\cos\theta-\sin2\theta\sin\theta \\[4pt]&=(2\cos^2\theta-1)\cos\theta-2\sin\theta\cos\theta\cdot\sin\theta \\[4pt]&=2\cos^3\theta-\cos\theta-2(1-\cos^2\theta)\cos\theta \\[4pt]&=4\cos^3\theta-3\cos\theta
\end{align*}
$\sin3\theta$ も同様に考えると\cos3\theta&=\cos(2\theta+\theta) \\[4pt]&=\cos2\theta\cos\theta-\sin2\theta\sin\theta \\[4pt]&=(2\cos^2\theta-1)\cos\theta-2\sin\theta\cos\theta\cdot\sin\theta \\[4pt]&=2\cos^3\theta-\cos\theta-2(1-\cos^2\theta)\cos\theta \\[4pt]&=4\cos^3\theta-3\cos\theta
\end{align*}
\begin{align*}
\sin3\theta&=\sin(2\theta+\theta) \\[4pt]&=\sin2\theta\cos \theta+\cos2\theta\sin \theta \\[4pt]&=2\sin \theta\cos^2\theta+(1-2\sin^2\theta)\sin \theta \\[4pt]&=2\sin \theta(1-\sin^2\theta)+\sin \theta-2\sin^3\theta \\[4pt]&=3\sin \theta-4\sin^3\theta
\end{align*}
\sin3\theta&=\sin(2\theta+\theta) \\[4pt]&=\sin2\theta\cos \theta+\cos2\theta\sin \theta \\[4pt]&=2\sin \theta\cos^2\theta+(1-2\sin^2\theta)\sin \theta \\[4pt]&=2\sin \theta(1-\sin^2\theta)+\sin \theta-2\sin^3\theta \\[4pt]&=3\sin \theta-4\sin^3\theta
\end{align*}

ヒロ
(2)は図を描いて状況を把握しよう。
【(2)の解答】
点Qの座標は $(\cos(-3\theta),~\sin(-3\theta))$ と表すことができ,$0<\theta<\dfrac{\pi}{6}$ のとき,$-\dfrac{\pi}{2}<-3\theta<0$ であるから,点Qは原点を中心とする単位円周上の第4象限の部分にある。よって,下図のようになる。
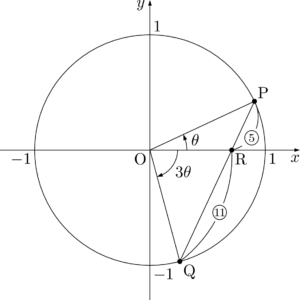
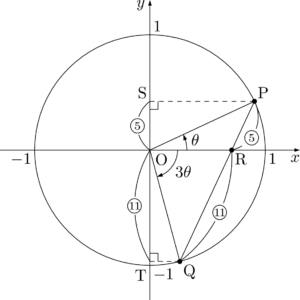
2点P, Qから $y$ 軸に下ろした垂線の足をそれぞれS, Tとすると,$\mathrm{SO:OT}=5:11$ となる。
したがって,符号に注意すると
点Qの座標は $(\cos(-3\theta),~\sin(-3\theta))$ と表すことができ,$0<\theta<\dfrac{\pi}{6}$ のとき,$-\dfrac{\pi}{2}<-3\theta<0$ であるから,点Qは原点を中心とする単位円周上の第4象限の部分にある。よって,下図のようになる。

2点P, Qから $y$ 軸に下ろした垂線の足をそれぞれS, Tとすると,$\mathrm{SO:OT}=5:11$ となる。

したがって,符号に注意すると
\begin{align*}
&\sin\theta:\sin3\theta=5:11 \\[4pt]&5\sin3\theta=11\sin\theta
\end{align*}
(1)の結果を用いると&\sin\theta:\sin3\theta=5:11 \\[4pt]&5\sin3\theta=11\sin\theta
\end{align*}
\begin{align*}
&5(3\sin\theta-4\sin^3\theta)=11\sin\theta \\[4pt]&20\sin^3\theta-4\sin\theta=0 \\[4pt]&\sin\theta(5\sin^2\theta-1)=0
\end{align*}
$0<\theta<\dfrac{\pi}{6}$ のとき,$0<\sin\theta<\dfrac{1}{2}$ であるから&5(3\sin\theta-4\sin^3\theta)=11\sin\theta \\[4pt]&20\sin^3\theta-4\sin\theta=0 \\[4pt]&\sin\theta(5\sin^2\theta-1)=0
\end{align*}
\begin{align*}
\sin\theta=\dfrac{1}{\sqrt{5}}
\end{align*}
また,$\cos\theta>0$ より\sin\theta=\dfrac{1}{\sqrt{5}}
\end{align*}
\begin{align*}
\cos\theta&=\sqrt{1-\sin^2\theta} \\[4pt]&=\sqrt{1-\left(\dfrac{1}{\sqrt{5}}\right)^2} \\[4pt]&=\dfrac{2}{\sqrt{5}}
\end{align*}
\cos\theta&=\sqrt{1-\sin^2\theta} \\[4pt]&=\sqrt{1-\left(\dfrac{1}{\sqrt{5}}\right)^2} \\[4pt]&=\dfrac{2}{\sqrt{5}}
\end{align*}

工夫しないと大変ですね。

ヒロ
そうだね。線分の長さの比が与えられているからといって,線分の長さを求めて,方程式を立てると大変なことになる。座標軸と平行になっていない線分の長さの比を,座標軸と平行な線分の長さの比に変換して考えることができるようにしよう。

ヒロ
最後の(3)はどうやって解く?

(3)の $\sankaku{POR}$ の面積を求める方法として,2つの方法が考えられます。

ヒロ
その2つの方法はどんなの?

1つはORの長さを求めて $\sankaku{POR}$ を求める方法で,もう1つは $\sin4\theta$ を求めて $\sankaku{POQ}$ の面積を経由する方法です。

まずは1つ目の解法で解いてみます。
【(3)ORの長さを求める解法】
点RはPQを $5:11$ に内分するから
点RはPQを $5:11$ に内分するから
\begin{align*}
\Vec{OR}=\dfrac{11}{16}\Vec{OP}+\dfrac{5}{16}\Vec{OQ}
\end{align*}
ORの長さは $\Vec{OR}$ の $x$ 成分であるから\Vec{OR}=\dfrac{11}{16}\Vec{OP}+\dfrac{5}{16}\Vec{OQ}
\end{align*}
\begin{align*}
\mathrm{OR}&=\dfrac{1}{16}(11\cos\theta+5\cos3\theta) \\[4pt]&=\dfrac{1}{16}\{11\cos\theta+5(4\cos^3-3\cos\theta)\} \\[4pt]&=\dfrac{1}{4}(5\cos^3\theta-\cos\theta) \\[4pt]&=\dfrac{1}{4}\left\{5\left(\dfrac{2}{\sqrt{5}}\right)^3-\dfrac{2}{\sqrt{5}}\right\} \\[4pt]&=\dfrac{1}{4}\Cdot\dfrac{6}{\sqrt{5}} \\[4pt]&=\dfrac{3}{2\sqrt{5}}
\end{align*}
したがって\mathrm{OR}&=\dfrac{1}{16}(11\cos\theta+5\cos3\theta) \\[4pt]&=\dfrac{1}{16}\{11\cos\theta+5(4\cos^3-3\cos\theta)\} \\[4pt]&=\dfrac{1}{4}(5\cos^3\theta-\cos\theta) \\[4pt]&=\dfrac{1}{4}\left\{5\left(\dfrac{2}{\sqrt{5}}\right)^3-\dfrac{2}{\sqrt{5}}\right\} \\[4pt]&=\dfrac{1}{4}\Cdot\dfrac{6}{\sqrt{5}} \\[4pt]&=\dfrac{3}{2\sqrt{5}}
\end{align*}
\begin{align*}
\sankaku{POR}&=\dfrac{1}{2}\Cdot\mathrm{OP}\Cdot\mathrm{OR}\sin\theta \\[4pt]&=\dfrac{1}{2}\Cdot\dfrac{3}{2\sqrt{5}}\Cdot\dfrac{1}{\sqrt{5}} \\[4pt]&=\dfrac{3}{20}
\end{align*}
\sankaku{POR}&=\dfrac{1}{2}\Cdot\mathrm{OP}\Cdot\mathrm{OR}\sin\theta \\[4pt]&=\dfrac{1}{2}\Cdot\dfrac{3}{2\sqrt{5}}\Cdot\dfrac{1}{\sqrt{5}} \\[4pt]&=\dfrac{3}{20}
\end{align*}

次に,もう1つの解法で解きます。
【(3)$\sin4\theta$ を求める解法】
(2)の結果より
(2)の結果より
\begin{align*}
\sin4\theta&=2\sin2\theta\cos2\theta \\[4pt]&=4\sin\theta\cos\theta(\cos^2\theta-\sin^2\theta) \\[4pt]&=4\Cdot\dfrac{1}{\sqrt{5}}\Cdot\dfrac{2}{\sqrt{5}}\left\{\left(\dfrac{2}{\sqrt{5}}\right)^2-\left(\dfrac{1}{\sqrt{5}}\right)^2\right\} \\[4pt]&=\dfrac{8}{5}\Cdot\dfrac{3}{5} \\[4pt]&=\dfrac{24}{25}
\end{align*}
となるから\sin4\theta&=2\sin2\theta\cos2\theta \\[4pt]&=4\sin\theta\cos\theta(\cos^2\theta-\sin^2\theta) \\[4pt]&=4\Cdot\dfrac{1}{\sqrt{5}}\Cdot\dfrac{2}{\sqrt{5}}\left\{\left(\dfrac{2}{\sqrt{5}}\right)^2-\left(\dfrac{1}{\sqrt{5}}\right)^2\right\} \\[4pt]&=\dfrac{8}{5}\Cdot\dfrac{3}{5} \\[4pt]&=\dfrac{24}{25}
\end{align*}
\begin{align*}
\sankaku{OPQ}&=\dfrac{1}{2}\Cdot\mathrm{OP}\Cdot\mathrm{OQ}\sin4\theta \\[4pt]&=\dfrac{1}{2}\Cdot\dfrac{24}{25} \\[4pt]&=\dfrac{12}{25}
\end{align*}
$\mathrm{PR:RQ}=5:11$ より\sankaku{OPQ}&=\dfrac{1}{2}\Cdot\mathrm{OP}\Cdot\mathrm{OQ}\sin4\theta \\[4pt]&=\dfrac{1}{2}\Cdot\dfrac{24}{25} \\[4pt]&=\dfrac{12}{25}
\end{align*}
\begin{align*}
\sankaku{POR}&=\dfrac{5}{16}\sankaku{OPQ} \\[4pt]&=\dfrac{5}{16}\Cdot\dfrac{12}{25} \\[4pt]&=\dfrac{3}{20}
\end{align*}
\sankaku{POR}&=\dfrac{5}{16}\sankaku{OPQ} \\[4pt]&=\dfrac{5}{16}\Cdot\dfrac{12}{25} \\[4pt]&=\dfrac{3}{20}
\end{align*}

労力としては,それほど変わらなかったみたいです。

ヒロ
今回の問題のように,$\mathrm{PR:RQ}$ が与えられていれば,その比を利用する解法を選択する人が多いだろうね。

そう思います。ベクトルを利用しなかったらORの長さを求めるのに苦労しそうです。

ヒロ
そうだね。あと数年経てば,ベクトルは理系専用になってしまうから,解くための道具が少なくなって,文系生は苦労するかもしれない。

恐ろしい時代がやってきますね・・・



















