ここでは,一般角の三角関数について説明します。
三角比の単元では角の範囲を0°~180°(0~πラジアン)で考えたが,三角関数ではその範囲に留まらず180°(πラジアン)より大きい角はもちろん,360°(2πラジアン)以上の角も扱います。
また,0°より小さい負の角を考えることもあります。
負の角や360°以上の角については,0°以上360°未満の角に変換して考えることが基本となります。
正の角・負の角・一般角

ヒロ
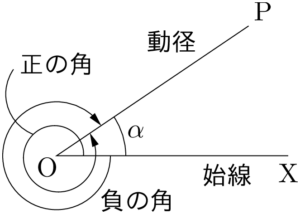
これまでは角と言えば2つの直線で作られる角を考え,その大きさだけを扱ってきたが,向きも考えることにすることで「正の角」と「負の角」を扱うことができるようになる。

ヒロ
反時計回りに測った角が正の角であり,時計回りに測った角が負の角である。
一般角始線OXから動径OPまでの角を測るとき,1回転以上しても良いことにすると,例えば,$\kaku{XOP}=\alpha$ のとき,動径OPが表す角 $\theta$ は $n$ を整数として
\begin{align*}
\theta=\alpha+2n\pi
\end{align*}
と表すことができる。\theta=\alpha+2n\pi
\end{align*}

三角関数の定義

ヒロ
三角比の記事で三角比の定義をしたが,扱う角が一般角となるため,様々な角の $\sin\theta$,$\cos\theta$,$\tan\theta$ の値を扱えるようになる。

ヒロ
定義があやふやな人は次の記事を読んで復習しておこう。

ヒロ
一般角の三角関数の値について,次のことが成り立つ。
一般角の三角関数の値
- $\sin(\theta+2n\pi)=\sin\theta$
- $\cos(\theta+2n\pi)=\cos\theta$
- $\tan(\theta+n\pi)=\tan\theta$
※ $n$ は整数とする。

ヒロ
$\sin\theta$ と $\cos\theta$ については $2\pi$ の整数倍だけずれても動径の位置は変わらないことを意識しよう。

ヒロ
$\tan\theta$ については,傾きを意識することで $\pi$ の整数倍ずれても値が変わらないことが理解できるだろう。
一般角に関する問題【2008年 北海道工業大】
2008年 北海道工業大次の三角関数の値を答えよ。
(1) $\cos\dfrac{100}{3}\pi$ (2) $\tan\dfrac{100}{3}\pi$
(1) $\cos\dfrac{100}{3}\pi$ (2) $\tan\dfrac{100}{3}\pi$
【(1)の考え方と解答】
角を0以上 $2\pi$ 未満にしよう。
角を0以上 $2\pi$ 未満にしよう。
\begin{align*}
\dfrac{100}{3}\pi&=2\pi\times16+\dfrac{4}{3}\pi
\end{align*}
であるから\dfrac{100}{3}\pi&=2\pi\times16+\dfrac{4}{3}\pi
\end{align*}
\begin{align*}
\cos\dfrac{100}{3}\pi&=\cos\dfrac{4}{3}\pi=-\dfrac{1}{2}
\end{align*}
\cos\dfrac{100}{3}\pi&=\cos\dfrac{4}{3}\pi=-\dfrac{1}{2}
\end{align*}
(2) $\tan\dfrac{100}{3}\pi$
【(2)の考え方と解答】
角は(1)と同じなので,サクッと求めよう。
角は(1)と同じなので,サクッと求めよう。
\begin{align*}
\tan\dfrac{100}{3}\pi&=\tan\dfrac{4}{3}\pi=\sqrt{3}
\end{align*}
\tan\dfrac{100}{3}\pi&=\tan\dfrac{4}{3}\pi=\sqrt{3}
\end{align*}



















