Contents
2020年 一橋大
2020年 一橋大$a$ を定数とし,$0\leqq\theta<\pi$ とする。方程式
\begin{align*} \tan2\theta+a\tan\theta=0 \end{align*}
を満たす $\theta$ の個数を求めよ。【考え方と解答】
定数を含む方程式の解の個数を調べるときは「定数を分離する」ことが1つの考え方である。ただ,そのまま定数を分離して「$a=-\dfrac{\tan2\theta}{\tan\theta}$」と変形しても $y=(右辺)$ のグラフを描くのは大変である。
したがって,2倍角の公式を用いて $\theta$ に揃えよう。$\tan2\theta+a\tan\theta=0$ より
$a\neq0$ のとき
$\dfrac{a+2}{a}=0$ となるのは,$a=-2$ のときであり,①をみたす $\theta$ は $\theta=0$ の1個である。また,$\dfrac{a+2}{a}>0$ となるのは $a<-2,~0<a$ のときであり,①をみたす $\theta$ は2個存在し,2個とも $\theta\neq0$ である。
以上より,求める $\theta$ の個数は次のようになる。
$a<-2,~0<a$ のとき3個
$-2\leqq a\leqq0$ のとき1個
定数を含む方程式の解の個数を調べるときは「定数を分離する」ことが1つの考え方である。ただ,そのまま定数を分離して「$a=-\dfrac{\tan2\theta}{\tan\theta}$」と変形しても $y=(右辺)$ のグラフを描くのは大変である。
したがって,2倍角の公式を用いて $\theta$ に揃えよう。$\tan2\theta+a\tan\theta=0$ より
\begin{align*} &\dfrac{2\tan\theta}{1-\tan^2\theta}+a\tan\theta=0 \\[4pt] &\tan\theta\left(\dfrac{2}{1-\tan^2\theta}+a\right)=0 \\[4pt] &\tan\theta=0~または~\dfrac{2}{1-\tan^2\theta}+a=0 \end{align*}
$\tan\theta=0$ のとき,$0\leqq\theta<\pi$ より,$\theta=0$ つまり,$a$ の値にかかわらず,与えられた方程式は1個の解をもつ。 $\dfrac{2}{1-\tan^2\theta}+a=0$ のときを考える。$y=(左辺)$ のグラフを描いて考えても良いが,$\tan^2\theta=(aの式)$ に変形できて,こちらの方が楽そうである。 \begin{align*} &2+a(1-\tan^2\theta)=0 \\[4pt] &a\tan^2\theta=a+2 \end{align*}
$a=0$ のとき,上の等式をみたす $\theta$ は存在しない。$a\neq0$ のとき
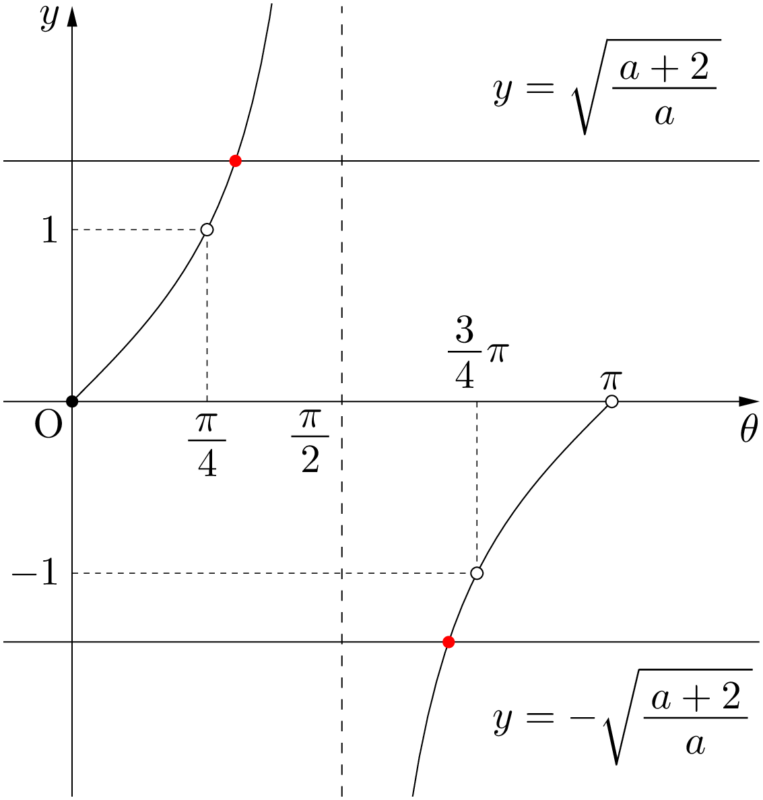
\begin{align*} &\tan^2\theta=\dfrac{a+2}{a} \\[4pt] &\tan\theta=\pm\sqrt{\dfrac{a+2}{a}}~\cdots\cdots① \end{align*}
$y=\tan\theta$ のグラフと $y=\pm\sqrt{\dfrac{a+2}{a}}$ のグラフの共有点を調べる。ここで $\dfrac{a+2}{a}<0$ となるのは $-2<a<0$ のときであり,このときは①をみたす $\theta$ は存在しない。
$\dfrac{a+2}{a}=0$ となるのは,$a=-2$ のときであり,①をみたす $\theta$ は $\theta=0$ の1個である。また,$\dfrac{a+2}{a}>0$ となるのは $a<-2,~0<a$ のときであり,①をみたす $\theta$ は2個存在し,2個とも $\theta\neq0$ である。
以上より,求める $\theta$ の個数は次のようになる。
$a<-2,~0<a$ のとき3個
$-2\leqq a\leqq0$ のとき1個


















