Contents
2018年 自治医科大
2018年 自治医科大$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ $(0\leqq\theta\leqq2\pi)$ を満たす $\theta$ の総和を $a$ とする。$\dfrac{2a}{\pi}$ の値を求めよ。
【解法のアプローチ】
$\theta$ の総和を求めないといけないため,具体的に $\theta$ を求めることを考える。方法としては次の3通りを思い浮かべるだろう。
- 3倍角の公式を利用して,角を $\theta$ に統一する
- 和積公式を利用して積の形にする
- 合成して和積公式を利用する
3倍角の公式を使うと,$\sin\theta,~\cos\theta$ の3次式になるから因数分解を考えることになるだろうと予想できる。
次に和積公式を利用するとどうなるかを考えてみる。左辺は「サインの差」だから $2cs$ となり,右辺は「コサインの和」だから $2cc$ となる。角は前から順に $2\theta,~\theta$ であるから,両辺に $\cos2\theta$ が現れることが分かる。つまり簡単に因数分解できることが暗算でも分かる。
合成する場合は $3\theta$ どうしを合成,$\theta$ どうしを合成すると解けることが予想できる。1つずつ順番に説明していく。
3倍角の公式を利用した解法

ヒロ
まずは3倍角の公式を利用して解いていく。
【3倍角の公式を利用した解法】
$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ より
$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ より
\begin{align*}
&3\sin\theta-4\sin^3\theta-\sin\theta=4\cos^3\theta-3\cos\theta+\cos\theta \\[4pt]
&4(\sin^3\theta+\cos^3\theta)-2(\sin\theta+\cos\theta)=0 \\[4pt]
&4(\sin\theta+\cos\theta)(1-\sin\theta\cos\theta)-2(\sin\theta+\cos\theta)=0 \\[4pt]
&(\sin\theta+\cos\theta)\{2(1-\sin\theta\cos\theta)-1\}=0 \\[4pt]
&\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)(\sin2\theta-1)=0 \\[4pt]
&\sin\left(\theta+\dfrac{\pi}{4}\right)=0~または~\sin2\theta=1
\end{align*}
$0\leqq\theta\leqq2\pi$ のとき,$\dfrac{\pi}{4}\leqq\theta+\dfrac{\pi}{4}\leqq2\pi+\dfrac{\pi}{4}$ であるから,$\sin\left(\theta+\dfrac{\pi}{4}\right)=0$ より&3\sin\theta-4\sin^3\theta-\sin\theta=4\cos^3\theta-3\cos\theta+\cos\theta \\[4pt]
&4(\sin^3\theta+\cos^3\theta)-2(\sin\theta+\cos\theta)=0 \\[4pt]
&4(\sin\theta+\cos\theta)(1-\sin\theta\cos\theta)-2(\sin\theta+\cos\theta)=0 \\[4pt]
&(\sin\theta+\cos\theta)\{2(1-\sin\theta\cos\theta)-1\}=0 \\[4pt]
&\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)(\sin2\theta-1)=0 \\[4pt]
&\sin\left(\theta+\dfrac{\pi}{4}\right)=0~または~\sin2\theta=1
\end{align*}
\begin{align*}
&\theta+\dfrac{\pi}{4}=\pi,~2\pi \\[4pt]
&\theta=\dfrac{3}{4}\pi,~\dfrac{7}{4}\pi
\end{align*}
$0\leqq2\theta\leqq4\pi$ であるから,$\sin2\theta=1$ より&\theta+\dfrac{\pi}{4}=\pi,~2\pi \\[4pt]
&\theta=\dfrac{3}{4}\pi,~\dfrac{7}{4}\pi
\end{align*}
\begin{align*}
&2\theta=\dfrac{\pi}{2},~\dfrac{5}{2}\pi \\[4pt]
&\theta=\dfrac{\pi}{4},~\dfrac{5}{4}\pi
\end{align*}
よって,$\theta=\dfrac{\pi}{4},~\dfrac{3}{4}\pi,~\dfrac{5}{4}\pi,~\dfrac{7}{4}\pi$ となるから&2\theta=\dfrac{\pi}{2},~\dfrac{5}{2}\pi \\[4pt]
&\theta=\dfrac{\pi}{4},~\dfrac{5}{4}\pi
\end{align*}
\begin{align*}
\dfrac{2a}{\pi}&=\dfrac{2}{\pi}\left(\dfrac{\pi}{4}+\dfrac{3}{4}\pi+\dfrac{5}{4}\pi+\dfrac{7}{4}\pi\right) \\[4pt]
&=\dfrac{2}{\pi}\Cdota4\pi \\[4pt]
&=8
\end{align*}
\dfrac{2a}{\pi}&=\dfrac{2}{\pi}\left(\dfrac{\pi}{4}+\dfrac{3}{4}\pi+\dfrac{5}{4}\pi+\dfrac{7}{4}\pi\right) \\[4pt]
&=\dfrac{2}{\pi}\Cdota4\pi \\[4pt]
&=8
\end{align*}
和積公式を利用した解法

ヒロ
次は和積公式を利用して解いていく。
【和積公式を利用した解法】
$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ より
グラフより,$\theta=\dfrac{\pi}{4},~\dfrac{5}{4}\pi$
これ以降は上と同じだから省略する。
$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ より
\begin{align*}
&2\cos2\theta\sin\theta=2\cos2\theta\cos\theta \\[4pt]
&\cos2\theta(\sin\theta-\cos\theta)=0 \\[4pt]
&\cos2\theta=0~または~\sin\theta=\cos\theta
\end{align*}
$0\leqq2\theta\leqq4\pi$ であるから,$\cos2\theta=0$ より&2\cos2\theta\sin\theta=2\cos2\theta\cos\theta \\[4pt]
&\cos2\theta(\sin\theta-\cos\theta)=0 \\[4pt]
&\cos2\theta=0~または~\sin\theta=\cos\theta
\end{align*}
\begin{align*}
&2\theta=\dfrac{\pi}{2},~\dfrac{3}{2}\pi,~\dfrac{5}{2}\pi,~\dfrac{7}{2}\pi \\[4pt]
&\theta=\dfrac{\pi}{4},~\dfrac{3}{4}\pi,~\dfrac{5}{4}\pi,~\dfrac{7}{4}\pi
\end{align*}
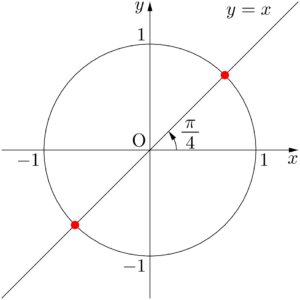
$\cos\theta=x$,$\sin\theta=y$ とおくと $\sin\theta=\cos\theta$ の解は,直線 $y=x$ と円 $x^2+y^2=1$ の交点を考えることで求めることができる。&2\theta=\dfrac{\pi}{2},~\dfrac{3}{2}\pi,~\dfrac{5}{2}\pi,~\dfrac{7}{2}\pi \\[4pt]
&\theta=\dfrac{\pi}{4},~\dfrac{3}{4}\pi,~\dfrac{5}{4}\pi,~\dfrac{7}{4}\pi
\end{align*}

グラフより,$\theta=\dfrac{\pi}{4},~\dfrac{5}{4}\pi$
これ以降は上と同じだから省略する。
合成を利用した解法

ヒロ
合成を利用した解法で解いていく。
【合成を利用した解法】
$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ より
$\sin3\theta-\sin\theta=\cos3\theta+\cos\theta$ より
\begin{align*}
&\sin3\theta-\cos3\theta=\sin\theta+\cos\theta \\[4pt]
&\sqrt{2}\sin\left(3\theta-\dfrac{\pi}{4}\right)=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)
\end{align*}
よって,整数 $n$ を用いると&\sin3\theta-\cos3\theta=\sin\theta+\cos\theta \\[4pt]
&\sqrt{2}\sin\left(3\theta-\dfrac{\pi}{4}\right)=\sqrt{2}\sin\left(\theta+\dfrac{\pi}{4}\right)
\end{align*}
\begin{align*}
&3\theta-\dfrac{\pi}{4}=\theta+\dfrac{\pi}{4}+2n\pi,~\pi-\left(\theta+\dfrac{\pi}{4}\right)+2n\pi \\[4pt]
&\theta=\dfrac{\pi}{4}+n\pi,~\dfrac{\pi}{4}+\dfrac{n}{2}\pi
\end{align*}
$0\leqq\theta\leqq2\pi$ より&3\theta-\dfrac{\pi}{4}=\theta+\dfrac{\pi}{4}+2n\pi,~\pi-\left(\theta+\dfrac{\pi}{4}\right)+2n\pi \\[4pt]
&\theta=\dfrac{\pi}{4}+n\pi,~\dfrac{\pi}{4}+\dfrac{n}{2}\pi
\end{align*}
\begin{align*}
\theta=\dfrac{\pi}{4},~\dfrac{3}{4}\pi,~\dfrac{5}{4}\pi,~\dfrac{7}{4}\pi
\end{align*}
先程と同様,これ以降は同じなので省略する。\theta=\dfrac{\pi}{4},~\dfrac{3}{4}\pi,~\dfrac{5}{4}\pi,~\dfrac{7}{4}\pi
\end{align*}

ヒロ
それぞれの解法に好き嫌いはあるかもしれないが,どれでも出来るようにするのが良いだろう。



















