ここでは樹形図を用いて場合の数を求める方法を説明します。
まず「場合の数」とは何かを理解しましょう。
例えば,1つのさいころを振ったとき,その目の出方は1, 2, 3, 4, 5, 6の6通りあります。
また,ジョーカーを含むトランプ53枚から1枚を選んだとき,そのカードの選び方は53通りあります。
このように,ある事柄の起こり得る場合の総数を「場合の数」といいます。
この「場合の数」を正しく求めるためには「書き出す」ことが基本となります。
ただし思い付くまま書くのでは書き漏れや重複が発生する可能性があるため,もれなく重複なくすべてを書き出す方法を身に付けることが重要です。
Contents
樹形図を利用しよう

もれなく重複なくすべてを書き出す方法の1つに「樹形図」を用いる方法がある。

実際に定期テストで出題された次の問題で説明する。

1文字目を何にするかはa, b, cの3通りがあるが,「bが多いからbから書く」というのではない。

もれなく重複なく描くためには,自分で規則を定めて描くのが基本。

今回はアルファベットを扱うので「アルファベット順」で描いていこう。

つまり1文字目をaにしよう。2文字目と3文字目もアルファベット順で考えよう。
1文字目がaの場合,aが1つしかないから,2文字目をbにする。
3文字目はbのときとcのときがあるから文字列は次のようになる。
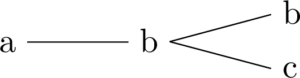
このように樹木が枝分かれしているような様子から樹形図と呼ばれる。
次に2文字目がcの場合も考えて,aから始まる文字列は次のようになる。
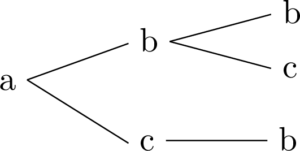
これで1文字目がaの場合が終わったから,次は1文字目がbの場合を考える。
同じようにアルファベット順を意識すると次の図のようになる。
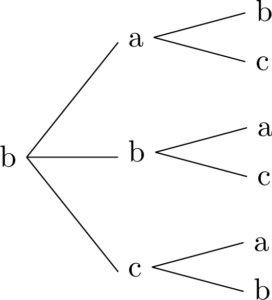
最後に1文字目がcの場合を考えると次のようになる。
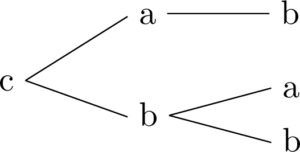
これでもれなく重複なく書き出すことができたから,全部で12通りあると分かる。
樹形図を用いて場合の数を求める問題

それでは実際に定期テストで出題された問題を解いてみよう。

「表」や「裏」と書くと時間がかかる。

「オ」と「ウ」でも良いが,まだ少し画数が多いのと,何回も書いているとゲシュタルト崩壊を起こしたりするので「○」と「×」を書くのがオススメ。
ゲシュタルト崩壊とは,知覚における現象のひとつ。
全体性を持ったまとまりのある構造(Gestalt, 形態)から全体性が失われてしまい,個々の構成部分にバラバラに切り離して認識し直されてしまう現象をいう。幾何学図形,文字,顔など,視覚的なものがよく知られているが,聴覚や皮膚感覚においても生じうる。

また「○」と「×」では「○」を優先して書くことにする。

ここで「表」を「○」とすると,○と×を書いていって○か×が3回出たところで終了することを考えて樹形図を描いていこう。
○と×を書いていって○か×が3回出たところで終了することを考えて,○から始まる樹形図を描くと次のようになる。
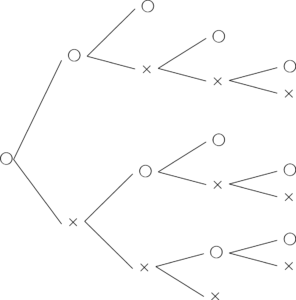
○から始まるものは全部で10通りあると分かる。
「×から始まるものも調べるのか」と嘆く人がいるかもしれないが,その必要はない。
○と×を入れ換えれば良いだけだから,×から始まるものも10通りあると分かる。
したがって,全部で20通り。

追加説明をしておくと,○と×をそもそも入れ換える必要すらない。

「○」を「表」,「×」を「裏」だと見たが,「○」を「裏」,「×」を「表」だと見れば良いだけのことだね。

○と×を使うことで,表と裏を意識する必要がなくなるのが大きなメリットであるため,是非この考え方を身に付けて欲しい。


















