上の画像のように,水が入った透明なグラスを通して見ると,グラスの向こう側にある物体が本来ある位置とは異なる位置に見えたり,小さく見えたりします。これは光が異なる2つの媒質を進むときに屈折する性質があるからです。
ここでは,光がもつ性質の1つである屈折の法則とも呼ばれるスネルの法則と,それに関する入試問題について説明します。
理系の方は理科で物理を選択する方が多いと思います。物理で光の屈折について学ぶとき,スネルの法則(屈折の法則)の公式については,その原理をしっかりと理解することなく,ただ覚えているだけになっている人も多いのではないでしょうか。
数学の入試問題として出題されたスネルの法則に関する問題を解くことで,何故スネルの法則が成り立つのか理解しましょう。
スネルの法則とは
スネルの法則波がある媒質中を進んでいて,途中で別の媒質に変化したとき,その境界面において,波の速度と入射角・屈折角が変化することがあります。
二つの異なる媒質中(媒質1と媒質2)を進む波の速度 $v_1,~v_2$ と入射角 $\theta_1$,屈折角 $\theta_2$ には,
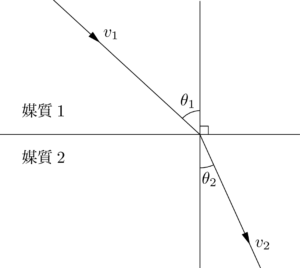
二つの異なる媒質中(媒質1と媒質2)を進む波の速度 $v_1,~v_2$ と入射角 $\theta_1$,屈折角 $\theta_2$ には,
\begin{align*}
\dfrac{\sin\theta_1}{\sin\theta_2}=\dfrac{v_1}{v_2}
\end{align*}
の関係が成り立ち,この法則をスネルの法則(屈折の法則)という。\dfrac{\sin\theta_1}{\sin\theta_2}=\dfrac{v_1}{v_2}
\end{align*}

スネルの法則に関する入試問題【2004年 滋賀県立大】
2004年 滋賀県立大$xy$ 平面上に点 $\mathrm{A}(0,~a)$ $(a>0)$,$\mathrm{B}(b,~c)$ $(b>c,~c<0)$ および $\mathrm{T}(t,~0)$ がある。いま,動点Pが,AからTまで線分AT上を一定の速さ $u$ で進み,ただちにTからBまで線分TB上を一定の速さ $v$ で進む。ただし,Tは,PがAからTを経由してBに達するまでに要する時間が最小となるように定めてあるとする。
(1) 点 $\mathrm{C}(t,~a)$ と点 $\mathrm{D}(t,~c)$ を与えて,$\kaku{ATC}$ および $\kaku{BTD}$ をそれぞれ $\alpha,~\beta$ としたとき,$\dfrac{u}{v}$ を $\alpha,~\beta$ で表せ。
(2) $u$ および $v$ があらゆる正の実数を動くとき,$t$ のとり得る値の範囲を求めよ。
(1) 点 $\mathrm{C}(t,~a)$ と点 $\mathrm{D}(t,~c)$ を与えて,$\kaku{ATC}$ および $\kaku{BTD}$ をそれぞれ $\alpha,~\beta$ としたとき,$\dfrac{u}{v}$ を $\alpha,~\beta$ で表せ。
(2) $u$ および $v$ があらゆる正の実数を動くとき,$t$ のとり得る値の範囲を求めよ。

ヒロ
まずは図を描いて状況を把握しよう。
【状況を把握するための図】
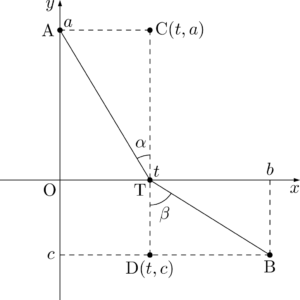

ヒロ
PがAからTを経由してBまで進む時間が最小になる条件を考えれば良いね。
【(1)の解答】
ATとBTの長さは
ATとBTの長さは
\begin{align*}
&\mathrm{AT}=\sqrt{t^2+a^2} \\[4pt]
&\mathrm{BT}=\sqrt{(t-b)^2+c^2}
\end{align*}
となるから,PがTを経由してBまで進む時間を $f(t)$ とすると&\mathrm{AT}=\sqrt{t^2+a^2} \\[4pt]
&\mathrm{BT}=\sqrt{(t-b)^2+c^2}
\end{align*}
\begin{align*}
f(t)&=\dfrac{\mathrm{AT}}{u}+\dfrac{\mathrm{BT}}{v} \\[4pt]
&=\dfrac{\sqrt{t^2+a^2}}{u}+\dfrac{\sqrt{(t-b)^2+c^2}}{v}
\end{align*}
f(t)&=\dfrac{\mathrm{AT}}{u}+\dfrac{\mathrm{BT}}{v} \\[4pt]
&=\dfrac{\sqrt{t^2+a^2}}{u}+\dfrac{\sqrt{(t-b)^2+c^2}}{v}
\end{align*}

ヒロ
$f(t)$ が最小になるときを考えるので,微分して調べよう。
【(1)の解答の続き】
したがって,$f(t)$ は $t=t_0$ で最小となる。$f'(t_0)=0$ より
\begin{align*}
f'(t)&=\dfrac{t}{u\sqrt{t^2+a^2}}+\dfrac{t-b}{v\sqrt{(t-b)^2+c^2}}
\end{align*}
ここで,$t\leqq0$ のときは $f'(t)<0$ であり,$t\geqq b$ のときは $f'(t)>0$ であるから,$0<t<b$ で調べる。$0<t<b$ のとき,$f'(t)$ をf'(t)&=\dfrac{t}{u\sqrt{t^2+a^2}}+\dfrac{t-b}{v\sqrt{(t-b)^2+c^2}}
\end{align*}
\begin{align*}
f'(t)=\dfrac{1}{u\sqrt{1+\dfrac{a^2}{t^2}}}+\dfrac{1}{v\sqrt{1+\dfrac{c^2}{(t-b)^2}}}
\end{align*}
と変形すると,$0<t<b$ において $f'(t)$ が単調に増加することが分かる。また,$f'(0)<0,~f'(b)>0$ であり $f'(t)$ は連続であるから,$f'(t_0)=0$ を満たす $t_0~(0<t_0<b)$ がただ1つ存在する。f'(t)=\dfrac{1}{u\sqrt{1+\dfrac{a^2}{t^2}}}+\dfrac{1}{v\sqrt{1+\dfrac{c^2}{(t-b)^2}}}
\end{align*}
したがって,$f(t)$ は $t=t_0$ で最小となる。$f'(t_0)=0$ より
\begin{align*}
&\dfrac{t_0}{u\sqrt{{t_0}^2+a^2}}+\dfrac{t_0-b}{v\sqrt{(t_0-b)^2+c^2}}=0 \\[4pt]
&\dfrac{\sin\alpha}{u}-\dfrac{\sin\beta}{v}=0 \\[4pt]
&\dfrac{u}{v}=\dfrac{\sin\alpha}{\sin\beta}
\end{align*}
&\dfrac{t_0}{u\sqrt{{t_0}^2+a^2}}+\dfrac{t_0-b}{v\sqrt{(t_0-b)^2+c^2}}=0 \\[4pt]
&\dfrac{\sin\alpha}{u}-\dfrac{\sin\beta}{v}=0 \\[4pt]
&\dfrac{u}{v}=\dfrac{\sin\alpha}{\sin\beta}
\end{align*}

ヒロ
(2)を解いてみよう。
【(2)の解答】
$u>0,~v>0$ のとき,$\dfrac{u}{v}>0$ となるから,(1)の結果より
$u>0,~v>0$ のとき,$\dfrac{u}{v}>0$ となるから,(1)の結果より
\begin{align*}
\dfrac{\sin\alpha}{\sin\beta}>0
\end{align*}
が成り立つ。したがって,\dfrac{\sin\alpha}{\sin\beta}>0
\end{align*}
\begin{align*}
&\dfrac{t_0}{\sqrt{{t_0}^2+a^2}}\Cdota\dfrac{\sqrt{(b-t_0)^2+c^2}}{t_0-b}>0 \\[4pt]
&\dfrac{t_0}{b-t_0}>0 \\[4pt]
&0<t_0<b
\end{align*}
よって,求める $t$ のとり得る値の範囲は,&\dfrac{t_0}{\sqrt{{t_0}^2+a^2}}\Cdota\dfrac{\sqrt{(b-t_0)^2+c^2}}{t_0-b}>0 \\[4pt]
&\dfrac{t_0}{b-t_0}>0 \\[4pt]
&0<t_0<b
\end{align*}
\begin{align*}
0<t<b
\end{align*}
0<t<b
\end{align*}
スネルの法則に関する入試問題のまとめ

ヒロ
スネルの法則は,物理選択者にとっては,覚えていて当然の法則ではあるが,今回のように,数学の入試問題として出題されることがあるのも知っておこう。

ヒロ
また,今回紹介した滋賀県立大以外にも,同じ2004年の九州大でも出題されている。また,スネルの法則に関連した問題は,2006年東京工業大,2007年に九州工業大でも出題されている。

ヒロ
いつ出題されても対応できるようにしておこう。


















