ここでは2次不等式の応用について説明します。
主に2次方程式の解に関する条件が与えられた問題では,判別式の符号を考えることによって不等式を解く場合があります。
その不等式が2次不等式になることもあります。
落ち着いて対応できるようにしましょう。
2次方程式の解に関する問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題2次不等式 $x^2-(m-3)x+m^2+2m+1\leqq0$ が解をもたないような,定数 $m$ の値の範囲を求めよ。
【考え方と解答】
「2次不等式が解をもたない」の意味が分からない人にとってはかなり難しい問題だろう。2次不等式と2次関数のグラフには密接な関係がある。
こう言うと「グラフを考えるのが思いつかない」と言われることがあるが,思い付くとか思い付かないとかいう話ではない。
2次不等式の解を考えるなら,グラフを考えて当然という状態になるようにするだけである。
「食事前に手を洗う」「就寝前に歯を磨く」のように,やって当然の状態にすると良い。
2次関数のグラフを見た上で,2次不等式を解くのなら比較的簡単であるが,2次不等式の解の条件から2次関数のグラフがどのようになっているかを考えるのは少し難しい。別の記事にも載せたが,2次不等式の解についてまとめた表をもう一度載せておく。

「2次不等式 $x^2-(m-3)x+m^2+2m+1\leqq0$ の解がない」ときがどんなときか分かるだろう。
$C:y=x^2-(m-3)x+m^2+2m+1$ のグラフは下に凸の放物線であるから,$x$ 軸から浮いた状態になれば良いことが分かるはず。しかし「なるほど!これで分かった!もう大丈夫!」と思わない方が良い。
今はグラフを見せたから分かっただけで,実際に問題を解いているときには,グラフを見ていないのだから,その状態でもグラフを考えてどのような状態になっているかを考えないといけない。スムーズに解けるようになるには2次関数のグラフと2次不等式の関係の理解が必須である。
それでは「放物線 $C$ が $x$ 軸から浮いた状態」を数式で表そう。
これは放物線と2次方程式の関係に着目して考える。$C$ が $x$ 軸から浮いた状態にあるということは,$C$ が $x$ 軸と共有点をもたないということであるから,2次方程式 $x^2-(m-3)x+m^2+2m+1=0$ が実数解をもたないということである。すなわち,判別式を $D$ とすると,$D<0$ となる。
この言い換えをスムーズにできるようになろう。
「2次不等式が解をもたない」の意味が分からない人にとってはかなり難しい問題だろう。2次不等式と2次関数のグラフには密接な関係がある。
こう言うと「グラフを考えるのが思いつかない」と言われることがあるが,思い付くとか思い付かないとかいう話ではない。
2次不等式の解を考えるなら,グラフを考えて当然という状態になるようにするだけである。
「食事前に手を洗う」「就寝前に歯を磨く」のように,やって当然の状態にすると良い。
2次関数のグラフを見た上で,2次不等式を解くのなら比較的簡単であるが,2次不等式の解の条件から2次関数のグラフがどのようになっているかを考えるのは少し難しい。別の記事にも載せたが,2次不等式の解についてまとめた表をもう一度載せておく。

「2次不等式 $x^2-(m-3)x+m^2+2m+1\leqq0$ の解がない」ときがどんなときか分かるだろう。
$C:y=x^2-(m-3)x+m^2+2m+1$ のグラフは下に凸の放物線であるから,$x$ 軸から浮いた状態になれば良いことが分かるはず。しかし「なるほど!これで分かった!もう大丈夫!」と思わない方が良い。
今はグラフを見せたから分かっただけで,実際に問題を解いているときには,グラフを見ていないのだから,その状態でもグラフを考えてどのような状態になっているかを考えないといけない。スムーズに解けるようになるには2次関数のグラフと2次不等式の関係の理解が必須である。
それでは「放物線 $C$ が $x$ 軸から浮いた状態」を数式で表そう。
これは放物線と2次方程式の関係に着目して考える。$C$ が $x$ 軸から浮いた状態にあるということは,$C$ が $x$ 軸と共有点をもたないということであるから,2次方程式 $x^2-(m-3)x+m^2+2m+1=0$ が実数解をもたないということである。すなわち,判別式を $D$ とすると,$D<0$ となる。
この言い換えをスムーズにできるようになろう。
\begin{align*} &D=(m-3)^2-4(m^2+2m+1)<0 \\[4pt] &(m-3)^2-4(m+1)^2<0 \\[4pt] &\{(m-3)+2(m+1)\}\{(m-3)-2(m+1)\}<0 \\[4pt] &(3m-1)(-m-5)<0 \\[4pt] &(3m-1)(m+5)>0 \\[4pt] &x<-5,~\dfrac{1}{3}<m \end{align*}
※一度展開してから因数分解しても良い。2次方程式の解に関する問題2

ヒロ
次も定期テストで出題された問題。
問題すべての実数 $x$ に対して,2次不等式 $x^2-x\geqq mx-1$ が成り立つような定数 $m$ の値の範囲を求めよ。

ヒロ
与えられた条件の意味を考えて解こう。
【考え方と解答】
$f(x)=x^2-(m+1)x+1$ とおくと,与えられた条件は「すべての実数 $x$ に対して,$f(x)\geqq0$ が成り立つ」となる。$C:y=f(x)$ のグラフに着目すると,与えられた条件を満たすのは,放物線 $C$ が $x$ 軸と接しているか,$x$ 軸より上側にあるような状態にあるときだと分かる。
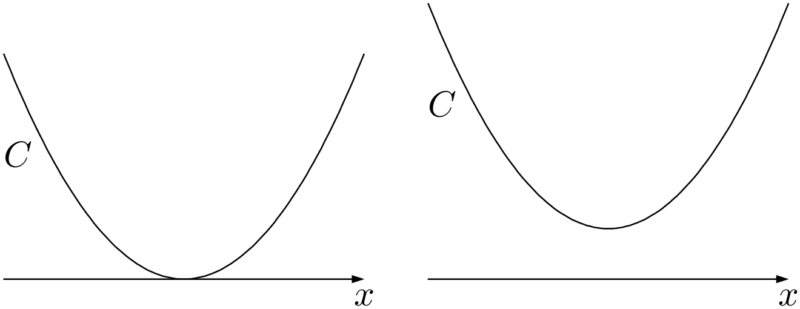
$f(x)=0$ の判別式を $D$ として,上の図の状態を $D$ を用いて表すと,左上の図は $D=0$ であり,右上の図は $D<0$ である。したがって,$D\leqq0$ と表すことができる。
$f(x)=x^2-(m+1)x+1$ とおくと,与えられた条件は「すべての実数 $x$ に対して,$f(x)\geqq0$ が成り立つ」となる。$C:y=f(x)$ のグラフに着目すると,与えられた条件を満たすのは,放物線 $C$ が $x$ 軸と接しているか,$x$ 軸より上側にあるような状態にあるときだと分かる。

$f(x)=0$ の判別式を $D$ として,上の図の状態を $D$ を用いて表すと,左上の図は $D=0$ であり,右上の図は $D<0$ である。したがって,$D\leqq0$ と表すことができる。
\begin{align*} &D=(m+1)^2-4\leqq0 \end{align*}
平方完成されているから,展開せずに不等式を解こう。 \begin{align*} &(m+1)^2\leqq4 \\[4pt] &-2\leqq m+1\leqq2 \\[4pt] &-3\leqq m\leqq1 \end{align*}
2次方程式の解に関する問題3

ヒロ
次も定期テストで出題された問題。
問題2次方程式 $x^2+(k-1)x-ka=0$ が,すべての実数 $k$ に対して,異なる2つの実数解をもつという。このとき,定数 $a$ の満たす条件を求めよ。
【考え方と解答】
条件がややこしく感じる場合は,1つずつ丁寧に考えよう。
今回の場合は,「すべての実数 $k$ に対して」という部分については後で考えることにして,「2次方程式 $x^2+(k-1)x-ka=0$ が異なる2つの実数解をもつ」条件を考えよう。判別式を $D$ とすると,$D>0$ となることが分かる。つまり,$D$ を用いて問題文を読み替えると「すべての実数 $k$ に対して $D>0$ が成り立つ」となる。$D$ を求めると
これは文字が $k$ だから考えにくいのかもしれない。ちなみに $k$ を $x$ に変えると
「すべての実数 $x$ に対して $x^2+2(2a-1)x+1>0$ が成り立つ」
となる。「これなら分かる!」となる人は,文字の見た目に注意することで今後は難なく解けるだろう。逆に「文字が変わっただけでは分からない!」という人に対してはさらなる言い換えが必要となる。
「$x$ の不等式 $x^2+2(2a-1)x+1>0$ の解がすべての実数となる」
これで分かるだろうか?2次不等式の解が「すべての実数」となるのは $C:y=x^2+2(2a-1)x+1$ のグラフがどのようになるときかを考えよう。
実際,グラフに着目すると,放物線 $C$ が次のように $x$ 軸より上側にあるようになっているときに条件を満たすことが分かる。

では,この状態を数式を用いて表そう。
最初の問題と同様に,$C$ が $x$ 軸と共有点をもたないことに着目すると,$x^2+2(2a-1)x+1=0$ が実数解をもたないことが分かる。よって,この方程式の判別式を $D_2$ とすると $D_2<0$ となる。
条件がややこしく感じる場合は,1つずつ丁寧に考えよう。
今回の場合は,「すべての実数 $k$ に対して」という部分については後で考えることにして,「2次方程式 $x^2+(k-1)x-ka=0$ が異なる2つの実数解をもつ」条件を考えよう。判別式を $D$ とすると,$D>0$ となることが分かる。つまり,$D$ を用いて問題文を読み替えると「すべての実数 $k$ に対して $D>0$ が成り立つ」となる。$D$ を求めると
\begin{align*}
D&=(k-1)^2+4ka \\[4pt]
&=k^2+2(2a-1)k+1
\end{align*}
となるから,「すべての実数 $k$ に対して $k^2+2(2a-1)k+1>0$ が成り立つ」ような $a$ の条件を考える。D&=(k-1)^2+4ka \\[4pt]
&=k^2+2(2a-1)k+1
\end{align*}
これは文字が $k$ だから考えにくいのかもしれない。ちなみに $k$ を $x$ に変えると
「すべての実数 $x$ に対して $x^2+2(2a-1)x+1>0$ が成り立つ」
となる。「これなら分かる!」となる人は,文字の見た目に注意することで今後は難なく解けるだろう。逆に「文字が変わっただけでは分からない!」という人に対してはさらなる言い換えが必要となる。
「$x$ の不等式 $x^2+2(2a-1)x+1>0$ の解がすべての実数となる」
これで分かるだろうか?2次不等式の解が「すべての実数」となるのは $C:y=x^2+2(2a-1)x+1$ のグラフがどのようになるときかを考えよう。
実際,グラフに着目すると,放物線 $C$ が次のように $x$ 軸より上側にあるようになっているときに条件を満たすことが分かる。

では,この状態を数式を用いて表そう。
最初の問題と同様に,$C$ が $x$ 軸と共有点をもたないことに着目すると,$x^2+2(2a-1)x+1=0$ が実数解をもたないことが分かる。よって,この方程式の判別式を $D_2$ とすると $D_2<0$ となる。
\begin{align*} &\dfrac{D_2}{4}=(2a-1)^2-1<0 \\[4pt] &-1<2a-1<1 \\[4pt] &0<2a<2 \\[4pt] &0<a<1 \end{align*}


















