ここでは,定義域が動くような2次関数の最大値と最小値について説明します。
2次関数の最大値と最小値を求める問題では,軸と定義域の位置関係が重要です。
定義域が変わることによって,軸が定義域外になるかどうかに注目して考えられるようにしましょう。
定義域の中央が軸と重なるときが場合分けで重要な基準になります。
2次関数の最大値と最小値を求める問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題2次関数 $y=-x^2+4x$ の $a\leqq x\leqq a+2$ における関数の最大値が3であるような定数 $a$ の値を求めよ。

ヒロ
軸と定義域の位置関係に注目して場合分けしよう。
【考え方と解答】
$y=-x^2+4x$ より
また,どのような場合分けをしたとしても,$x=a,~a+2,~2$ のいずれかで最大となるから,それぞれの $y$ の値を求めておく。
$f(x)=-x^2+4x$ とおくと,
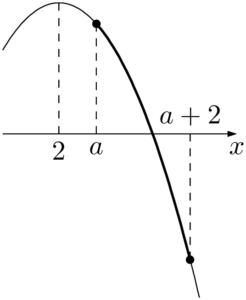
$x=a$ のとき最大値をとるから,最大値が3のとき
(ii) $a<2\leqq a+2$ すなわち $0\leqq a<2$ のとき
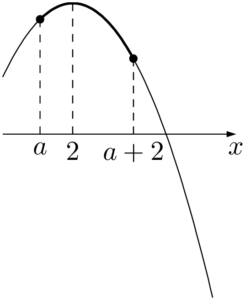
$x=2$ のとき最大値4をとるから,最大値が3となることはない。
(iii) $a+2\leqq2$ すなわち $a\leqq0$ のとき
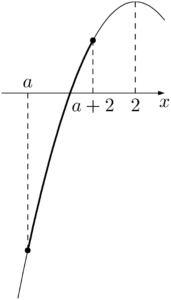
$x=a+2$ のとき最大値をとるから,最大値が3のとき
以上より,$a=-1,~3$
$y=-x^2+4x$ より
\begin{align*}
y=-(x-2)^2+4
\end{align*}
グラフは軸が $x=2$ の上に凸の放物線であるから,$x=2$ が定義域に含まれるときと含まれないときで場合分けをしよう。y=-(x-2)^2+4
\end{align*}
また,どのような場合分けをしたとしても,$x=a,~a+2,~2$ のいずれかで最大となるから,それぞれの $y$ の値を求めておく。
$f(x)=-x^2+4x$ とおくと,
\begin{align*}
&f(a)=-a^2+4a \\[4pt]
&f(a+2)=-(a+2)^2+4(a+2)=-a^2+4 \\[4pt]
&f(2)=4
\end{align*}
(i) $2\leqq a$ のとき&f(a)=-a^2+4a \\[4pt]
&f(a+2)=-(a+2)^2+4(a+2)=-a^2+4 \\[4pt]
&f(2)=4
\end{align*}

$x=a$ のとき最大値をとるから,最大値が3のとき
\begin{align*}
&-a^2+4a=3 \\[4pt]
&a^2-4a+3=0 \\[4pt]
&(a-1)(a-3)=0 \\[4pt]
&a=1,~3
\end{align*}
$2\leqq a$ より,$a=3$&-a^2+4a=3 \\[4pt]
&a^2-4a+3=0 \\[4pt]
&(a-1)(a-3)=0 \\[4pt]
&a=1,~3
\end{align*}
(ii) $a<2\leqq a+2$ すなわち $0\leqq a<2$ のとき

$x=2$ のとき最大値4をとるから,最大値が3となることはない。
(iii) $a+2\leqq2$ すなわち $a\leqq0$ のとき

$x=a+2$ のとき最大値をとるから,最大値が3のとき
\begin{align*}
&-a^2+4=3 \\[4pt]
&a^2=1 \\[4pt]
&a=\pm1
\end{align*}
$a\leqq0$ より,$a=-1$&-a^2+4=3 \\[4pt]
&a^2=1 \\[4pt]
&a=\pm1
\end{align*}
以上より,$a=-1,~3$
2次関数の最大値と最小値を求める問題2

ヒロ
次も実際に定期テストで出題された問題。
問題関数 $y=x^2-2x+3~(a\leqq x\leqq a+1)$ について次の問いに答えよ。
(1) 最小値を求めよ。またこのときの $x$ の値を求めよ。
(2) 最大値を求めよ。またこのときの $x$ の値を求めよ。
(1) 最小値を求めよ。またこのときの $x$ の値を求めよ。
(2) 最大値を求めよ。またこのときの $x$ の値を求めよ。

ヒロ
軸と定義域の位置関係に着目して場合分けをしよう。
【(1)の考え方と解答】
$y=x^2-2x+3$ より
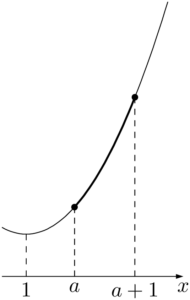
$x=a$ で最小値 $a^2-2a+3$ をとる。
(ii) $a\leqq 1<a+1$ すなわち $0<a\leqq1$ のとき
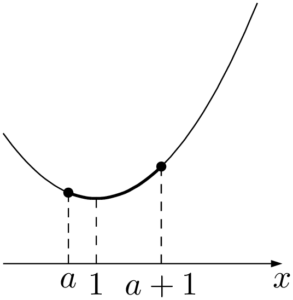
$y=x^2-2x+3$ より
\begin{align*}
y=(x-1)^2+2
\end{align*}
グラフは軸が $x=1$ の下に凸の放物線である。どの様に場合分けをしたとしても,$x=a,~a+1,~1$ のいずれかで最大・最小となるから,それぞれの$y$ の値を求めておく。$f(x)=x^2-2x+3$ とおくと,y=(x-1)^2+2
\end{align*}
\begin{align*}
&f(a)=a^2-2a+3 \\[4pt]
&f(a+1)=(a+1)^2-2(a+1)+3=a^2+2 \\[4pt]
&f(1)=2
\end{align*}
(i) $1<a$ のとき&f(a)=a^2-2a+3 \\[4pt]
&f(a+1)=(a+1)^2-2(a+1)+3=a^2+2 \\[4pt]
&f(1)=2
\end{align*}

$x=a$ で最小値 $a^2-2a+3$ をとる。
(ii) $a\leqq 1<a+1$ すなわち $0<a\leqq1$ のとき

$x=1$ で最小値 $2$ をとる。
(iii) $a+1\leqq1$ すなわち $a\leqq0$ のとき
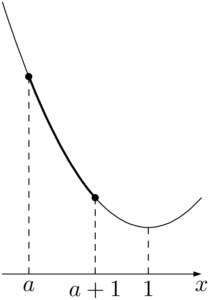

$x=a+1$ で最小値 $a^2+2$ をとる。
(2) 最大値を求めよ。またこのときの $x$ の値を求めよ。

ヒロ
軸と定義域の中央との位置関係に着目して場合分けしよう。
【(2)の考え方と解答】
(i) $1<a+\dfrac{1}{2}$ すなわち $\dfrac{1}{2}<a$ のとき


$x=a+1$ で最大値 $a^2+2$ をとる。
(ii) $a+\dfrac{1}{2}=1$ すなわち $a=\dfrac{1}{2}$ のとき
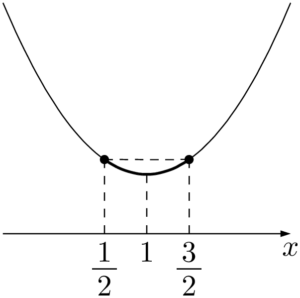

$x=\dfrac{1}{2},~\dfrac{3}{2}$ で最大値 $2$ をとる。
(iii) $a+\dfrac{1}{2}<1$ すなわち $a<\dfrac{1}{2}$ のとき


$x=a$ で最大値 $a^2-2a+3$ をとる。


















